
This blog post introduces a newly published book, titled "Maxwell-Dirac Theory and Occam's Razor: Unified Field, Elementary Particles, and Nuclear Interactions".
Science and technology generally evolve from simpler “low hanging fruits” towards more complex and intricate concepts. However, a change of perspective comes along from time to time, which allows some simplifications. The most well-known example is the pre-Newtonian Earth-centered perspective, where the motion of planets was described by epicycloid formulas. These formulas agreed with experimental data and the motion of planets was predictable. As the Sun-centered perspective became allowed, planetary motion was subsequently described by simpler elliptic formulas, which were manifestations of a universal gravitational force.
The history of physics may also be viewed as a progression from particle-oriented concepts to wave-oriented concepts. Over many centuries, scientists thought of light as a stream of small “light balls”. Then light was thought to be waves of aether particles, and finally just waves of the electromagnetic field. 100 years ago, the notion of elementary matter particles being quantum mechanical waves started gaining acceptance. The book which we introduce fits into this historic trend, and represents a next step in the understanding of wave-oriented concepts.
So where could a simplification possibly come from? A rational starting point is to look for the simplest relativistically compatible Lagrangian of a vector field. Its first-principles derivation can be found e.g. in chapter 19 of the "General Relativity: an Introduction for Physicists" book by M. P. Hobson et al. The authors then harshly treat this simplest Lagrangian: they throw it into the rubbish bin because it's not "gauge invariant". But electromagnetic gauge invariance is contradictory to Maxwell's equations (see e.g. arXiv:physics/0506203v1).
Therefore we reconsider this simplest Lagrangian, and further simplify things by not imposing electromagnetic gauge invariance. We use the intuitive language of geometric algebra, namely space-time Clifford algebra. We find that this electromagnetic Lagrangian corresponds to a familiar form of Maxwell’s equations: DA=G and DG=0, where A is the vector potential, D is the space-time differentiation operator, and G is the electromagnetic field. But there is big difference with respect to the usual form: G now incorporates electromagnetic fields, charges, and also currents. Wow, we no longer need to insert electric charges “by hand” into Maxwell’s equations? Indeed, charges and fields are now part of the same mathematical object. How’s that for a simplification?
We then test the theory by throwing it into deep water: can it also tell us what mass is made of? This is a swimming test which no theory passed yet, according to Feynman: “Many attempts have been made, and some of the theories were even able to arrange things so that all the electron mass was electromagnetic. But all of these theories have died”. By analyzing the relationship between the Maxwell and Dirac equations, we show that the mysterious “four-component Dirac spinor field” is nothing else than electromagnetic energy-momentum, whose dynamics is described by the Dirac equation. Subsequently, we derive from the model all the essential features of the electron: its mass exactly corresponds to its electromagnetic energy, its charge surface is on a sphere at the classical electron radius, its zitterbewegung (ZBW) radius is the reduced Compton radius (in the rest frame), we derive its relativistic increase of mass, show that its charge surface retains its spherical shape under any Lorentz boost, and obtain its correct magnetic moment and ZBW frequency as well.
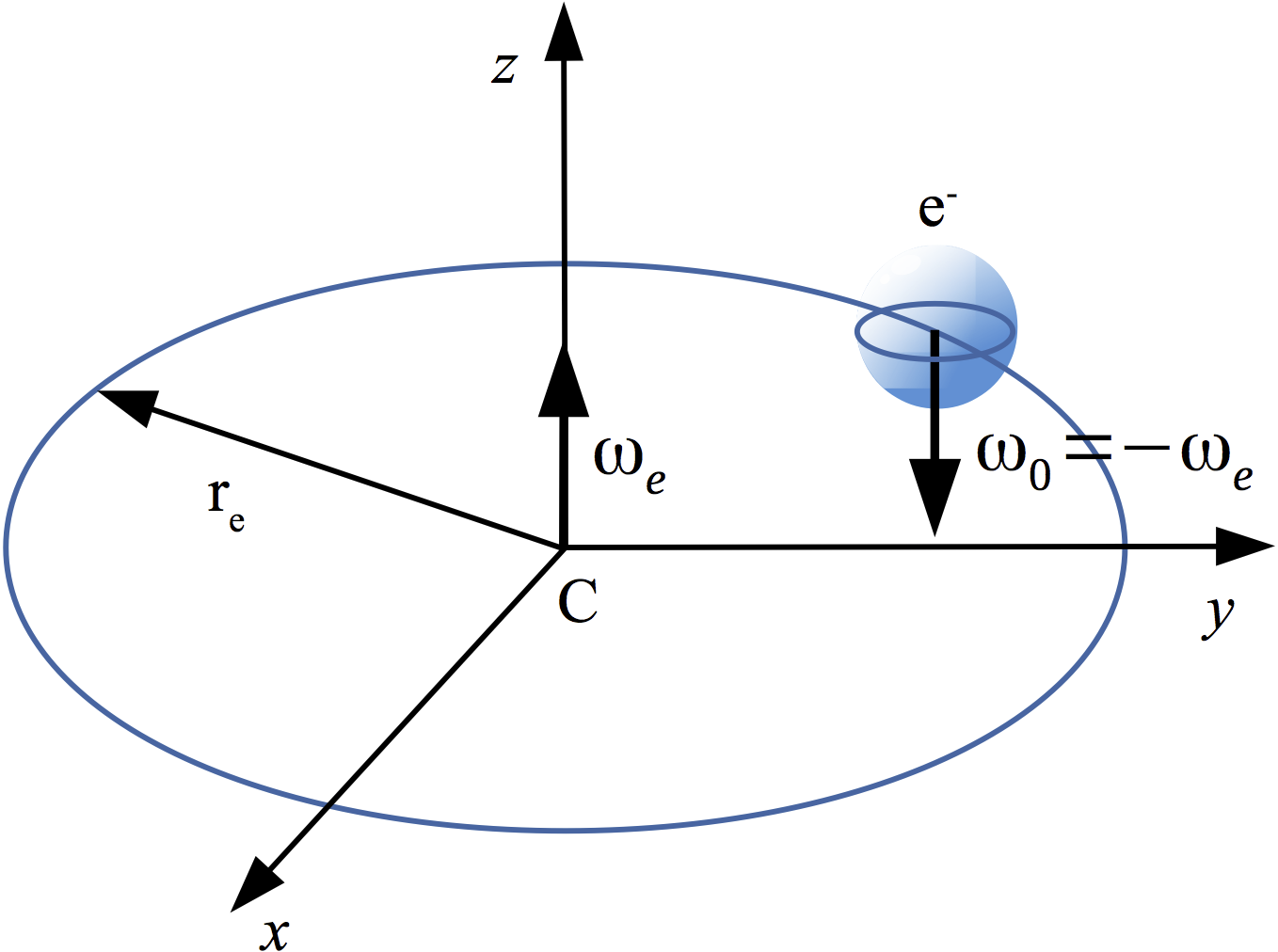
In other words, the book explains how electromagnetic fields comprise the electron mass. This resolves the mystery of what the electron mass is “made of”. The obtained electron structure is illustrated in the figure: the sphere represents its charge surface at 2.82 fm radius and the circle represents its 386 fm ZBW radius. Neither scale value is constant however, but inversely proportional to the electron energy. In this sense one cannot use high-energy scattering to measure “how large” the electron is, because with growing kinetic energy the outcome will show ever shrinking electron size.
At this point some readers may experience anxiety, thinking “is he going to say next that the electron is not an infinite electric field energy bearing abstract point, which gets blurred by Heisenberg uncertainty, and whose infinite field energy we are entitled to leave uncounted via renormalization?” Yes, that is exactly what our simplification states. There is no more need to see the electron as wave-function of infinitesimally small abstract points, and no more need to leave the corresponding infinite electric field energy uncounted.
Some skeptics might press on: “but the electron’s anomalous magnetic moment is calculated to 10 digits accuracy in QED, which proves that it is indeed an infinite electric energy bearing abstract point”. We would restate such claim as follows: for the purposes of many calculations, the electron can be represented by its center-of-mass. Rather than arguing this point, it’s more constructive to ask: in which calculations can the electron be represented by its center-of-mass, when it can’t be done, and why?
The uncovered electron geometry also sheds light onto a fundamental geometric scaling: the ratio between its charge radius and ZBW radius is exactly the fine structure constant, i.e. alpha. The ratio between its ZBW radius and Bohr radius is yet again alpha. We are back to the nearly 100 years old mystery regarding the origin of alpha, which seems very important for a true understanding of electromagnetism. How could we calculate its value from basic principles?
Although we do not resolve the mystery of alpha in the book, we point out some geometric constraints which appear to be relevant for charge quantization. Since the elementary charge and alpha are related via the h and c constants, understanding the charge quantization process is equivalent to discovering the origin of alpha.
The second part of the book investigates the broader consequences of the above results: what does this simplification imply for the range of possible electron orbits, what does it imply for nuclear electron capture, ...etc? These calculations make strong connection with experimental data, and uncover some surprising results, for example a new type of electron orbit. We anticipate this part to be of equal interest to theoretical and experimental physicists.
The book can found here



Comments