Now, the point of this article is to make sure you can USE the data you are able to get on the web. I use to say "there's not such a thing as too much information", but then I shoud qualify that statement: it all depends on whether you have a brain and a will to put it to work.
So if you think your brain is only a receptacle of your memories and feelings, then go ahead and pick the first restaurant in that damn list. You won't get choked with the food anyway, and that's maybe too bad, as it limits the speed at which evolution brings us forward as a sentient race.
Yes, this post is for those of you who are not afraid of using your naturally-given computing power. Now, the hotels and restaurants in TripAdvisor and elsewhere are rated by customers with 1- to 5-star reviews. The site will give you two crucial data about each rated element, and 99.9% of us only care to look at the first one: the average of those reviews. But the second one, my friends, is just as important as the first. That is the number of reviews themselves.
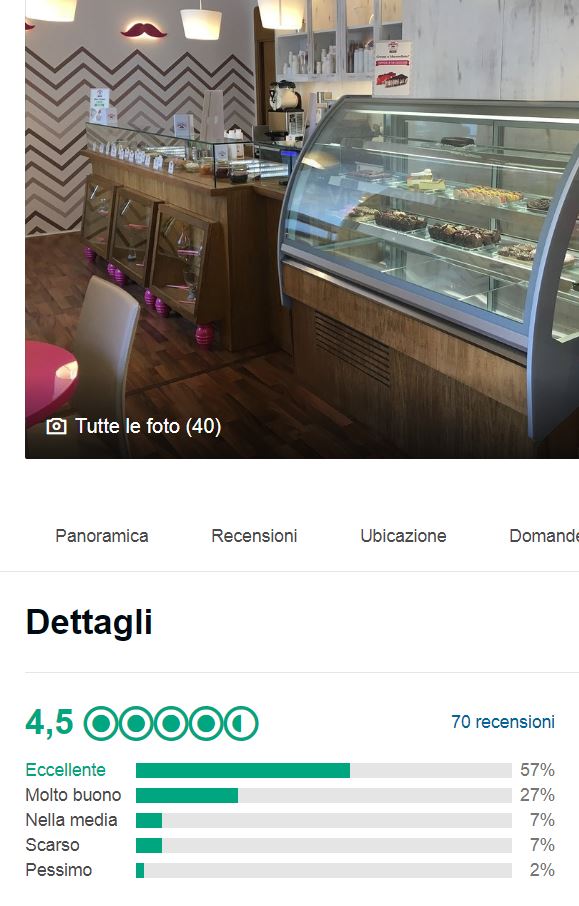In truth, the sites now give you still more than that. The distribution of scores, from 1 to 5 stars, is also provided. That information opens the way to much more detailed analysis than you will read about here. The reason is not that I would be unwilling to share what I do with that; it's only that the matter gets a bit too complicated for a blog post. It involves Winsorization and hypothesis testing, something that is really stuff for some other text.So, you have two numbers. To make it easy, and most useful, I will consider only a very special, but actually quite common, case: you narrowed down your search to two businesses (hotels or restaurants, whatever you are looking for), and need to pick one. Let us say you have business 1, with a score of 4.5 and 10 reviews, and business 2, with a score of 4.3 and 100 reviews. Which one offers the better chance of being a top choice?
First of all, we should say a couple of things about those reviews. It's quite dirty data. You have perhaps read about fake reviews being offered and bought by hotels and restaurants - in Italy they just jailed a few people who did exactly that for a living: forging reviews. But even forgetting about the pollution of 1- and 5-star reviews that comes from those illegitimate activities (Winsorization again comes to mind if you want to deal with those, but again let's forget the issue), reviewers are not computers - they're human beings, and they sometimes bring their evaluations to the extreme for one reason or another. But that's what we have: their output. We need to use it somehow.
One good rule of thumb, before we even start considering the example above, is to outright discard items that got less than five reviews. Anybody has five relatives who can write a review for their business; and even if those reviews were actually genuine, the uncertainty due to the smallness of the inputs is too high to read enough into the average.
Now, the two averages above have enough reviews each. Should we pick the business with the highest average? Well, again - most of us would do precisely that. But I claim that such a choice is not done in a well-informed way. Let me ask you the question: when you pick a hotel, do you actively try to get the best possible treatment, or are you rather trying to get a good one without any chance of it being a nightmare experience?
I believe that even if you are a 5+ star hotel goer, you are more concerned with avoiding total failures than nit-picking between Royal Palace and Hilton International. In other words, what you read into those reviews is not how close they are from a straight 5: you are trying to stay away from a very low actual rating, while choosing based on other criteria (how close to your travel goal, etc). If that applies to you, read on.
The point of this post is that customer reviews have a unknown probability distribution. If you know what a Binomial distribution is you might, upon knowing the boundaries of the problem (it's a score between 1 and 5, in integer steps) be tempted to think that the probability of a TripAdvisor score is binomially distributed around a certain unknown value ρ. Wrong. The behaviour of our reviewers follows no mathematical equation. So this is the first input: the average of N results has a unknown standard deviation. Not good - all those years of high school studies in the trash bin!
If the above is true, you could be justified in throwing your hands up and say "well then, WTF - I can't make sense of the uncertainty on those averages, so let's just pick the highest score". This is acceptable, but a bit defeatist. In fact, the central limit theorem comes to the rescue: as a first approximation, when you don't know what the data are sampled from, just assume that their average has a Gaussian distribution. This works astoundingly well with any probability distribution, in fact. To be honest, it is disturbingly wrong to use a Gaussian approximation in a bounded problem like that of a 1- to 5-star score, but here I want to give you some food for thought rather than being precise. We could discuss more accurate models but it's not the math level this post strives to get.
So let us go back to our data. We have enough reviews for each of the two businesses, and have no time to look into their distribution into actual 1-stars and 5-stars to make any preprocessing of the inputs. Should we pick business 1 or business 2? Well, again, arguing that what we care about is not how GOOD the business is, but rather how unlikely it is that it is actually a ripoff or a bad experience, I think what we need to do is to produce a LOWER LIMIT on the actual score of the business. And here, the uncertainties in those mean values play in.
Physicists do that all the time, by the way: we care about lower and upper limits of our confidence intervals, because we rely on those values, rather than the means of our data-driven results, to take decisions about the correctness of a physical models and stuff like that. What we ask ourselves, e.g., is "what is the value below which there's a less-than-2.5% probability that the real score of the business truly is that one, given the data?" This gives us confidence about the worst-case scenario, for 39 times out of 40 you are going to get a better actual score than that limiting value.
In the cases above business 1, despite having a higher mean rating (4.5), has an uncertainty of the mean which is larger, as it has been derived by averaging fewer inputs (10) than business 2 (4.3 with 101 reviews). For an estimate of the uncertainty of the mean we can take the root-mean-square of a uniformly distributed number from 1 to 5: this is the difference of the extrema divided by the square root of 12, so 4/sqrt(12)=1.1 or so. We can then obtain the uncertainty in the mean by dividing that result by the square root of the number of inputs minus one (10-1=9, whose square root is 3), getting 0.36.
A Gaussian curve with a mean of 4.5 and a sigma of 0.36 will have 2.5% of its integral below a score of 4.5-2*0.36=3.78. That is your safety limit with business 1: you might read it as "there's a less than 2.5% chance that the true score of business 1 is below 3.78", although you should be aware that it would be incorrect for a classical statistician to do that, as you are jumping from speaking of the probability of the data given a hypothesis to speaking of a probability of the hypothesis itself, something that only Bayesian statisticians venture to do. But fair enough, you got the point.
The same calculation on business 2 produces the result 4.3-2*(1.1/sqrt(99))=4.08. We don't need to be Bayesians to state a conclusion. The verdict is clear: the data we got are more probable if business 2 gives a lower chance of a disappointment. (see, I am not talking about probability of the two businesses scores!)
I hope the above discussion, while completely imprecise, will give you the stimulus to read a bit more carefully into the data you are showered with every day. For it IS possible to use it to your advantage, better than what the average user does. This is quite common and it is not an observation restricted to the TripAdvisor scores, of course. If you master some basic knowledge of statistics, you can become the one-eyed guy in a country of blind men.
----
Tommaso Dorigo is an experimental particle physicist who works for the INFN at the University of Padova, and collaborates with the CMS experiment at the CERN LHC. He coordinates the European network AMVA4NewPhysics as well as research in accelerator-based physics for INFN-Padova, and is an editor of the journal Reviews in Physics. In 2016 Dorigo published the book “Anomaly! Collider physics and the quest for new phenomena at Fermilab”. You can get a copy of the book on Amazon.
Comments