Therefore it makes sense to ask you, dear reader, what you think of the eerily arcane geometries that the system is proposing. I do not think that to be a good judge you need to know the details of how the model is put together, but I will nevertheless make an attempt at briefing you on it, just in case it makes a difference in your judgment.
What we are discussing is the problem of placing on the ground, at high altitude (4800 m) somewhere in the Andes, a set of detectors for cosmic ray particles. The detectors are 3.8m diameter units in the shape of cylindrical tanks filled with purified water that releases light by Cherenkov emission when energetic particles traverse them. The SWGO experiment plans to place 6000 of such tanks in an array that for the time being has been thought to have to be circular and tightly packed with detection units.
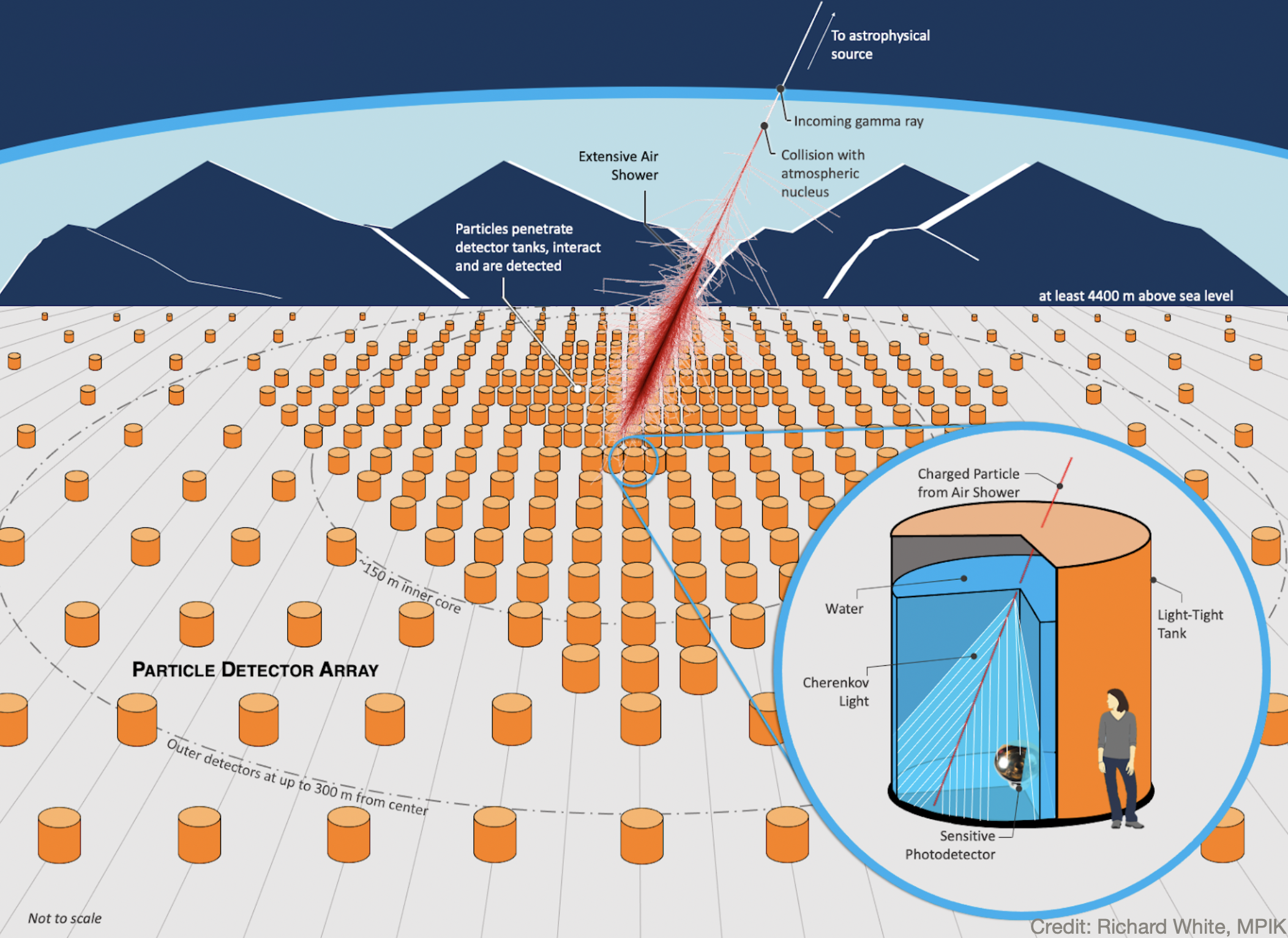
(Above, a graphical view of the SWGO conception. Credits: Richard White)
The problem of detecting the particle showers that energetic gamma rays produce when they hit the upper atmosphere is apparently a symmetric one - you have particles that may come down from any direction, all interesting. So a cylindrical symmetry seems to be implied. But if you have a finite number of units to place on the ground, you have to break that cylindrical symmetry somehow, making it discrete. Further, if you are more or less interested in wide or narrow showers (produced by particles of higher or lower energy), and if your reconstruction algorithm sets a minimum threshold on the number of detection units that see a coincidental signal in order to enable the reconstruction, and if the showers need to be discriminated at some high confidence from large backgrounds coming from proton-initiated showers - well, all those details will break the initial platonic symmetry of the problem. But what do they replace it with?
An AI may find out. So let us see what a "simple" 8000-lines-long C++ program that encodes detector geometry, shower reconstruction, inference extraction on the gamma-ray flux thinks about the most advantageous placement on the ground of 300 "macro-tanks", each made of 19 units packed into an hexagonal arrangement. The working with macro-units eases a bit the CPU-heavy task of simulating cosmic showers, reconstructing them, and finding the gradient of the utility function that the program must maximize by moving each unit a tiny little bit in the direction of improving the layout. An animated gif that shows the tanks moving around is shown below.
The second graph from the left on the top row is the one you want to set your eyes on. The black points show the location of macro-tanks on the ground, while the blue-green points that move around in a circle are the centers of generated cosmic-ray showers. As the system expands (to cover more ground, thereby measuring more showers per unit time and thus gaining scientific value), it also finds entirely non-trivial ways to improve the power of the reconstruction, and thus improve the utility function. The utility itself is shown on the leftmost graph. You can see it growing slowly but steadily. On the right of the layout graph is instead a histogram showing the radial position of the units, i.e. their distance from the center. The red histogram shows their initial distribution, and the blue one the distribution that the system is considering. The two graphs on the bottom row are instead more technical and I will just mention that they respectively show the energy resolution provided by the system on gamma showers as a function of gamma energy, and the test statistic used for discrimination of proton versus gamma showers.
So, what do you think of these geometries?





Comments