The Fermilab g-2 experiment has released today (April 7th, 5PM CET) its results on the measurement of the muon anomalous magnetic moment. The number they quote differs by 3.3 standard deviations from the theoretical prediction, and is in good agreement with the previous Brookhaven determination of the same quantity. The new result, therefore, is a nice confirmation that the effect first observed in 2001 is not of statistical nature, but has systematic origins. When combined, the two measurements average to a number which is at 4.2 standard deviations from theory predictions. The graph below summarizes the measurements and their departure from the theory (the band on the left).
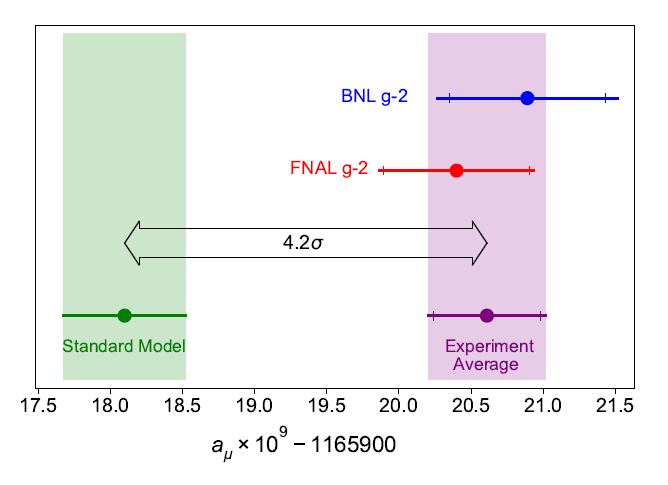
Mind you - when I say "systematic origins" I am not saying that a systematic uncertainty is the reason of the disagreement with theory. I am in fact saying that the effect is not a fluctuation, and it is rather due to a genuine difference - a systematic one - between what is measured and what is predicted. Indeed, the systematic uncertainties affecting the two experimental determinations are small and they should have no large effect in one's conclusions, unless one were willing to consider (correlated) effects of unknown origin in the two measurements, which I however deem rather unlikely.
So, the theory calculations - this is my interpretation - are estimating something slightly different from what the experiment is measuring. This is the essence of the observation. The difference may be due to a feature in the calculations -some approximations taken which are believed to have no impact but in fact do, e.g.- or to the absence of consideration of new forces of nature which may ever so slightly modify the behaviour of virtual photons from what the Standard Model predicts.
New Physics!?
New physics may be the culprit, indeed. Yet in an interview I gave to a freelance reporter yesterday, I summarized today's result rather cynically as "nothing new under the sun". Why? Am I such a disgruntled envious human being, who can't admit his colleagues' success? I dare say I am not. No - I am happy for them in fact. But with the interviewer I was rather trying to picture my line of reasoning with a one-liner. The new measurement confirms a previous one: so there is nothing new. The new result, once averaged with the previous one, produces a higher significance, but this does not reach the 5-sigma level which HEP physicists require to say that a new phenomenon has been proven "beyond reasonable doubt". So qualitatively, nothing is new under the sun.
Please appreciate that as scientists who talk to the media we have to always play it down a little, because anyway they'll add a little bit more punch. That's as precise a rule of Nature as the Standard Model.
So, nothing new under the sun. And yet, the result is a breath of fresh air for particle physics. For it keeps alive the hope that new physics is there to discover, and that therefore the effort to design and build new powerful colliders is justified. If you compare this situation with the alternative -say, if Fermilab had reported today a result that averaged the departure to a 1- or 1.5 sigma effect - you clearly see what I am trying to describe: that alternative universe would fill all particle physicists with a dose of gloom. Sure, there remain oddities in the measurements of universality that LHCb has been publishing as of late, which some of us (not me) are taking as a clear hint of new physics. But the g-2 anomaly has been the long-standing hope of new physics dreamers for a long time now, and nobody would have been happy to let that go.
Fitting details
In this short post I have no time to delve in the details of the measurement, but I will make a short note concerning the method used to analyse the data and extract the precession frequency of muon spins in the apparatus, from which the g-2 value is extracted. Mind you, the analysis is very complex and it is extremely well-done. But still, I remember listening to a presentation of the experiment in its early stages in Rome a year ago, when I was very surprised to learn that the collaboration was using a chisquare fit to Poisson-distributed data as their main analysis method. I had been quick to point out, back then, that this was suboptimal.
The reason why, at least in principle, a likelihood should be preferred is that here one knows the sampling distribution of the data in each bin of the histogram that is used by the fit (it is in this case a Poisson, as always happens when data come in at a constant rate independently). If you do not even have a hunch on what that distribution may be, using a chisquare minimization is reasonable, as it assumes Gaussian variates, which is a "failsafe" assumption, although an approximate one. But if you do, you better use it in the fit, and this will produce better results. But how much better? In fact, a Poisson distribution is known to converge to a Gaussian one for large number of events...
Now, in the paper that the g-2 collaboration has submitted for publication, the chisquare minimization method is still used to extract the measurement. Is this really suboptimal? In my utterly despicable presumptuousness, I decided to "test" this with a simulation. Beware, I do not assume that what I have been doing bears any relevance to the actual measurement: I am using mock data, cutting corners, and spending just one hour of my time to cook up a simple analysis macro. So take this as a simple exercise.
[In fact, this kind of fiddling with scientific results, trying to mock them, and playing with statistics is what I do for a living, when I teach my students to build their own critical thinking by experimenting with different assumptions etcetera...]
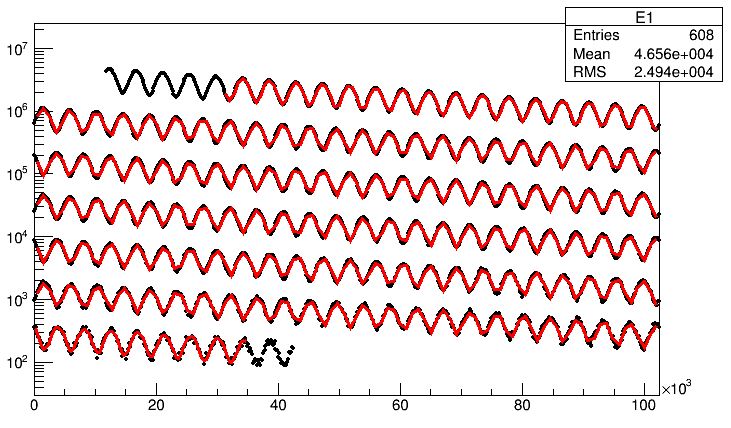
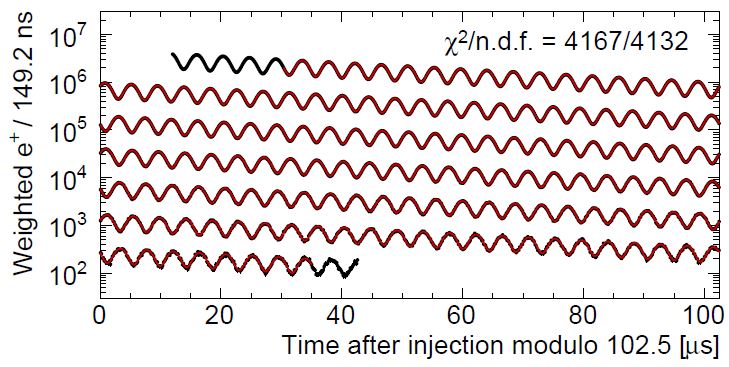
Above you can see the distribution of the data I produced (in black), with fit overimposed in red. - The data are divided into 4140 149.2-nanosecond-wide bins of observed electron counts, spanning 621 microseconds of time from 30 to 651 microseconds after the injection of muons in the apparatus. If you compare this graph to the one just released by the collaboration (see below), you will notice that it is in reasonable agreement with it - with which I am just saying that it is qualitatively comparable, nothing more.
I proceed to fit the distribution with the same functional form I employed for the data generation, using a chisquare minimization and a likelihood maximization, and obtain the following results for the parameter describing the sinusoidal modulation (which has a true value of 0.00144, in some random units):
chi2: 0.00143999 +- 9.28 E-9
likelihood: 0.00143999 +- 9.28 E-9
Great. I have to explain that I did not expect these two numbers to differ, in fact. The chisquare method assumes a Gaussian distribution in the number of fitted events in each bin (which is an approximation, as the data distribute as a Poisson, if we omit consideration of event weights, which I would have anyway no way of modeling in this quick check), and this is known to produce a "non-conservation" of the area under the histogram, with respect to a likelihood fit which is instead unbiased in the returned normalization; but a bias in a feature such as an oscillatory behavior is not to be expected, at least to first order. In any case, the g-2 experiment's statistics are so large that indeed, Poissons will be Gaussians at that point (beware, though, because even tiny differences in distribution functions may affect precision measurements more often than you would think!).
Indeed, even if we look at the total normalization parameter in my fit, and if I reduce by a factor of 100 the statistics (such that the above mentioned bias has a bigger play), I see the following:
chi2: 4.00465 E4 +- 1.588 E2
likelihood: 4.00085 E4 +- 1.588 E2
That is to say: nothing to see here either, walk on, please.
So, I rest my case. I hope my g-2 colleagues did consider the potential bias of using a chi2, and only after having done their homework they concluded as I am doing here that it was safe. But in any case, the result cannot be criticized on these grounds. In fact, it looks as it is a great piece of physics, so I am bound to congratulate with my colleagues from the collaboration for this exciting new result!
Original (pre-release) version, and explanation of the muon anomaly
At 5PM CET (11AM NY, 11PM Beijing) the Fermilab "g-2" experiment will release its most awaited results on the measurement of a quantity called "muon magnetic moment anomaly", and simultaneously, I will update this blog post to report on the released value.
But, why is that relevant, and why will it be so exciting to be updated on this measurement?
The muon
The muon is a heavier version of the electron. It is an elementary particle that is copiously produced when cosmic rays (protons and light nuclei) hit the upper atmosphere, create secondary hadrons, and the latter decay into muon-neutrino pairs. As we speak, and only slightly depending on your altitude over sea level and your geolocation, you are traversed by a few tens of muons every second. They whiz through the atoms of your body without leaving much behind - only some ionization trail, mostly, and each raises your body temperature by about a quadrillionth of a degree.
So, nothing to worry about, really. Furthermore, even if a muon stopped inside your body, it would soon decay (on average, you would have to wait about two microseconds for that to happen), releasing an electron and two neutrinos.
Muons can also be produced in laboratory. That is something that is routinely done in accelerator facilities such as the one at Fermilab. An intense beam of muons is used there as a source of the particles used by the g-2 experiment, which is basically a magnet wherein muons circulate and decay, and where their decay products are recorded.
Like electrons, muons are electromagnetically charged particles, and they are endowed with a quantity called "spin" - it is the quantum-mechanical analogue of the rotation of an object around itself. If you take a charged sphere and spin it, it generates a magnetic field - magnetic fields are in fact produced by moving electric charges. The same happens with the muon, due to its spin: it possesses an intrinsic "magnetic moment". Nobody can really explain how this makes sense for a point-like particle, as we describe the muon as voided of any spatial dimension; but the analogy between classical and quantum physics is strong enough that we accept the explanation. And in fact, we can measure this tiny magnetic moment. We do that by letting it interact with an external magnetic field, as it runs around the magnet.
The experiment records the precession of the muon spin around their orbit with extremely high accuracy, such that the magnetic moment of the particle can be extracted. We know the orientation of the magnetic moment when the muon is injected in the magnetic ring, because we know how to "polarize" the incoming beam such that the muon spins, and thus their magnetic moments, are aligned along some direction; and then we get to know the orientation when the muon finally decays, as depending on the spin orientation the muon emits the electron in different directions. By detecting those decay electrons as a function of time, we gain access to the muon precession, and measure it with extreme accuracy.
Quantum phenomena
The whole concept would be rather idle, were it not for the fact that the muon magnetic moment has a value slightly different from what its spin and charge would imply from a purely classical calculation. Indeed, "quantum corrections" affect that value. They arise because the interaction of magnetic fields of elementary particles takes place through the exchange of virtual photons, and those virtual photons can do a number of tricks while they're flying through. In the quantum world, a particle is never "just a bare particle": it in fact is better described as a cloud of virtual particles constantly emitted and reabsorbed, traveling along with their originator, the "bare particle" which provides the source of all the quantum fields that the cloud propagates.
One of the greatest triumphs of quantum mechanics was the demonstration that it is possible to compute the quantum corrections to things such as the magnetic moment of spinning elementary charges, due to those virtual clouds. In 1957 this was shown to be the case for the electron, by Feynman and Schwinger. They duly got a Nobel prize for that, and their result stands as one of the most astonishing demonstration of the powers of theoretical calculations: the measured value of the electron magnetic moment anomaly is known to less than a part in 10^12, and is in agreement with the theory prediction.
The same calculation, performed on the muon, yields a value which has been for the past 20 years in tension with the experimental determination (which was produced by the Brookhaven laboratories). Now, this is interesting, because a difference between the theory prediction and the measured value might be due to something missing in the theoretical calculation. If, e.g., a new force of nature were producing some tiny additional perturbations of the magnetic moment of the muon, by contributing with new actors to those virtual clouds, we would not observe an agreement in theory and experiment. Since the muon is heavier than the electron, such a discrepancy would be expected to be first observed in the muon.
New Physics?
The new determination of the muon anomaly, to be released today, promises to update our knowledge of the discrepancy between theory and experiment. The result is expected to have a similar sensitivity as the former one, so it may provide a confirmation of the Brookhaven result - which was an almost 4-standard-deviations effect - or partly cancel the disagreement.
One fun fact, incidentally, is that the magnet at the heart of the new experiment is the same one that was used for the previous measurement. This does not mean that there are large correlated systematics in the two determinations, however. The transportation of the large ring across the US, by boat and then by truck, has some epic flavour to it (see a pic of the thing being carried around, below).

Anyway, since both results are dominated by statistical precision, the new measurement will very likely tell us whether the old result was a fluctuation or not. Should the two results agree, what we would be looking at is a clear indication that there is a systematic effect at play: either a theoretical error in the calculation (like, e.g., some unaccounted-for, but mundane, effect), or the effect of new physics that the theory calculation is not including.
For a theorist, that would in any case be great news: one could then entertain in speculations of all kinds. It is a bit unfortunate, though, that the g-2 measurement is only one number: it is too little information of what that new physics could be, so it leaves open too many possibilities.
Furthermore, a single number off from predictions, for a theory of subnuclear processes (the Standard Model) which has withstood tests of astounding precision and verifications of predictions made 50 years back (just think at the Higgs boson, concocted in 1964 and discovered in 2012!), would not nearly be enough to declare that the theory is wrong. But for sure, if the g-2 result proves a 5-sigma departure from theoretical predctions, all claims that we need to push further with more precise and powerful investigations of the subnuclear world with new colliders and new experiments would gain substance.
So, please stay tuned! I will release the result in this blog very shortly after 5PM CET.
---
Tommaso Dorigo (see his personal web page here) is an experimental particle physicist who works for the INFN and the University of Padova, and collaborates with the CMS experiment at the CERN LHC. He coordinates the MODE Collaboration, a group of physicists and computer scientists from eight institutions in Europe and the US who aim to enable end-to-end optimization of detector design with differentiable programming. Dorigo is an editor of the journals Reviews in Physics and Physics Open. In 2016 Dorigo published the book "Anomaly! Collider Physics and the Quest for New Phenomena at Fermilab", an insider view of the sociology of big particle physics experiments. You can get a copy of the book on Amazon, or contact him to get a free pdf copy if you have limited financial means.






Comments