CONTENTS
PART A: Introduction: does the inertia of a body depend upon its energy content?
PART B: The Toolkit: mathematical and physical assumptions 
PART C: The Thought Experiment and the Word Problem
PART D: The Derivation. Solving the Word Problem
PART E: Conclusion: Einstein's Style or How to not be a Crack Pot


PART A:  Does the inertia of a body depend upon its energy content?

Students of physics know the answer to the question Einstein asked in the title of his celebrated paper, "Does the inertia of an object body depend upon its energy content?" because in it Einstein derived the equation . The inertia (or mass) of an object at rest is equal to  where E is the energy content of the object. A remarkable fact about this paper and many of his other early papers is their relative simplicity. I believe I can briefly state the few mathematical and physical assumptions used in the paper. These are conservation of energy, the principle of relativity, the formulas for the kinetic energy of a particle and the relativistic energy of light and the binomial theorem. Given these assumptions, and a cleverly devised thought experiment to apply them to, can be derived as though it were a simple undergraduate word problem. 

PART B: The Toolkit: Physical and Mathematical Assumptions

Physical Assumptions:

1. Conservation of Energy: Energy is neither created or destroyed. The total energy in an isolated system remains constant. In Einstein's thought experiment, the system consists of all the volume enclosing a box.

 

A classic example of conservation of energy. the pendulum
The bob of a pendulum has kinetic  and potential energy where m is the mass of the bob, v is its velocity, h is its height and g is a number that is determined by the strength of gravity. According to conservation of energy


  

As the bob ascends and its velocity decreases, h increases to keep the equation constant. When the height is maximum, the velocity is zero and when the height is zero, the velocity is maximized. As the bob swings back and forth, kinetic and potential energy vary, but the total energy of the system remains constant.

2. The relativistic equation for the energy of light

The energy  of a light ray in a frame moving with a constant velocity v can be determined from its energy in a stationary frame from 


[assuming the moving frame is parallel to the x-axis of the stationary frame and  is the angle of the light ray from the x-axis]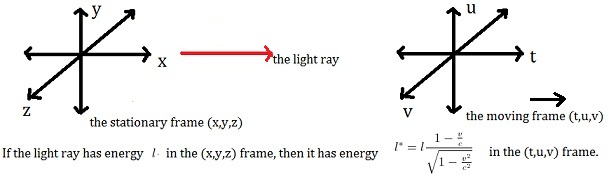

If the light ray is moving parallel with the x-axis and in the same direction as the moving reference frame then and cos(0)=1 and therefore


If the light ray were moving in the opposite direction, then (because cos(2*pi)=-1) the negative sign (-) before the v/c term is replaced by a positive sign(+). Einstein used this fact to simplify the mathematics of his derivation.

3. relativity: the freedom to choose different reference frames 

The principle of Special Relativity states that if a physical principle or equation holds in a stationary frame, it must also hold in a frame moving relative to it at constant velocity. We can evaluate a process from either reference frame. In the derivation of E=mc^2 below, the energy of a simple system is calculated in different frames of reference moving at constant velocity v relative to one another and, in accordance with the principle of relativity, it is assumed that the principle of conservation of energy holds equally in both frames of reference. 
4. kinetic energy As mentioned above, the kinetic energy of a particle with mass m, is  .

Mathematical Assumptions:

1. Elementary Algebra 

The Binomial Series:





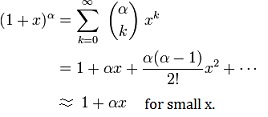
2. Calculus (optional)
The Taylor Series:

 
    
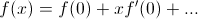
These assumptions (and keen physical intuition)  are all you need to derive E=mc^2. So, before I guide you through Einstein's derivation, try and derive it yourself. If I was a high school physics teacher I'd like to assign this word problem as extra credit. 


PART C: The Thought Experiment (applying mathematical and physical assumptions to a concrete scenerio) and the Word Problem:

Einstein began by constructing a simple thought experiment to apply his assumptions to.


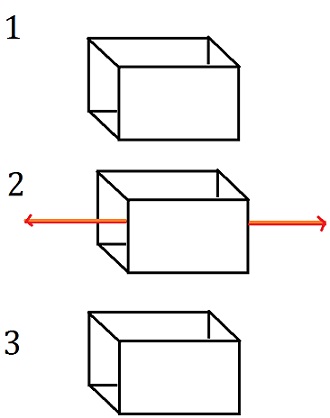1. A box is weighed. 

2. The box emits two, oppositely oriented, light rays for a short interval of time.

3. The box is weighed again. 

The Word Problem:

Has the box lost any mass as a result of the energy emitted from it? If so, how much?

Remember, light has no mass, therefore according the principle of mass conservation, no mass has left the box. 
In 1905, Lavoisier's principle of conservation of mass was still generally accepted. This 1905 Annus Mirabilis paper would overturn that.



A few remarks before presenting Einstein's derivation. 

On reducing a complicated problem to a problem that is "as simple as possible, but not simpler." Applying the mathematical and physical assumptions above to this simple thought experiment reduces the deep question Einstein posed in 1905 to a problem that an intelligent undergraduate physics student could answer. Notice that Einstein didn't attempt to argue from general principles. If you immediately plunged into the equations and started messing around with the math, then you are not thinking like Einstein. 

PART D: The Derivation. Solving the Word Problem 

The initial total energy of the box, relative to the stationary system (x,y,z), in Einstein's thought experiment is . This is the energy of the system, in the stationary frame, prior to the emission of the light rays.

The initial total energy of the box, relative to the moving frame (t,u,v), is  . This is the energy of the box, relative to the moving frame, prior to the emission of the light rays.  

If is the energy of the box, relative to the stationary frame, after the emission of the light rays and the total energy of both light rays is  then, by conservation of energy



If is the energy of the box, relative to the moving frame, after the emission of the light rays and the energy of the light rays in the moving frame is given by                           

  

then, by conservation of energy and the relativistic equation for the energy of light


and therefore



Einstein then calculates that



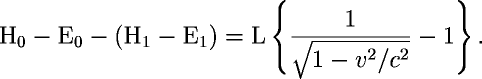
The first and second H-E terms on the left are measures of the change in energy of the box at the same instant in time due only to the relative motion of the two frames of reference. The first H-E term is the initial change in energy of the box due to relative motion of the two frames and the second term H-E term is the change in energy of the box after the emission of the light ray, but again, only due to the relative motion of the two frames. 

Because the H-E terms measure the change in energy of the box due to the relative motion of the two frames only, the additive constant C representing any other energy left over (such as the internal molecular energies of the box etc) is constant



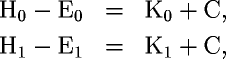
and therefore C cancels out leaving only the change in kinetic energy as



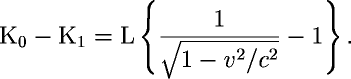
This can be approximated by the Binomial or Taylor Series "neglecting magnitudes of fourth order or higher." Applying the Binomial Theorem approximation above, 



therefore
 

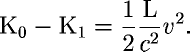
By comparing this to the expression for Kinetic energy  one can infer that the change in mass of the box due to the emission of light is equal to L/c^2. Recall that L is the total energy of the light rays emitted from the box, therefore E=mc^2. 

An Important Proviso: By using the binomial approximation in  this derivation, it was assumed that v < < c. If v were close to c, then this approximation would be invalid. This is why mc^2 is the rest energy of an object. The slower the box in the derivation is moving, the more accurate the approximation becomes. If an object is moving close to the speed of light, then the E=mc^2 approximation must be replaced by E^2 = (mc^2)^2 + (pc)^2 where p  is momentum.    

From this equation it directly follows that:—If a body gives off the energy L in the form of radiation, its mass diminishes by L/c². The fact that the energy withdrawn from the body becomes energy of radiation evidently makes no difference, so that we are led to the more general conclusion that the mass of a body is a measure of its energy-content; if the energy changes by L, the mass changes in the same sense by L/9 × 1020, the energy being measured in ergs, and the mass in grammes.                                                                                                                                                                              Einstein, Albert. Does the Inertia of a Body Depend upon its Energy Content?

PART E: Einstein's Style or How to not be a Crack Pot

In many of his papers Einstein derived general results by studying highly idealized thought experiments. He gave himself illuminating, but simple, word problems. In a great series of QFT lectures, Anthony Zee (see the suggestions section below) quotes Einstein as saying "Make physics as simple as possible, but not simpler." This was the approach of great physicists like Plank, Bohr and Feynman. Plank famously pioneered quantum mechanics by analyzing a box composed of small oscillators. At a Ted talk in honor of Feynman, Susskind said that Feynman was a master of simplifying physics. Compare this tendency with the grandiose complexity found in the work (and blog posts) of crack pots.

Now read the original paper. 

Questions

I'd like to inspire curiosity in my readers.  So here are some questions to ponder.

1. Did Einstein use the Taylor Series or the Binomial Series? Does his scratchwork still exist?
2. Did Einstein know the answer before deriving it or was he surprised by his own result? If so, why did he suspect that mass was related to energy?
3.What was the general consensus about the mass of light in 1900? What was Maxwell's opinion? 
4. I've stated some assumptions. Are there any "hidden assumptions" I've glossed over? 
5.What about those higher order terms in the Binomial expansion that I've ignored? 
6. Light always moves with the same speed and is always massless, but we have seen that light does have varying energy. This is different from the case of a particle. Why? 

Suggestions

Albert Einstein. Does the Inertia of a body depend upon its energy content? The original paper. 

Anthony Zee. Lectures on QFT. (with an emphasis on "making physics as simple as possible, but not simpler" especially in the lecture on "back of the envelop calculations") There also are many other excellent lecture series covering most of the major recent developments in physics including Dark Energy, Inflation, String Theory, and SUSY.

A Yale University Lecture on Taylor Series that includes a very brief derivation of E=mc^2 using Taylor Series. There are also very good lectures on Special Relativity in the same series especially this lecture on 4-Vectors.

In this MIT Lecture on Special Relativity Leonard Susskind derives E=mc^2 using the binomial theorem (at 1:16.00) and answers a question about the higher order terms of the binomial series approximation (at 1:22.40).