Or not true,
Or both true and not true,
Or neither true nor not true;
This is the Buddha's teaching.
--Nagarjuna (second century Buddhist monk and philosopher), the Mulamadhyamakakarika, Chapter XVIII, verse 8 (Note: there are other translations of this verse, for example, using "real" instead of "true.")
To a Western mind, this may seem like complete nonsense. True and not true are mutually exclusive and exhaustive states for any proposition--in fact, the law of the excluded middle, as this idea is expressed in mathematics, is the basis for much of (a certain kind of) proof theory. If you disallow it, proof by contradiction would not hold, and many theorems in mathematics would be unproved and undecided. So, what's behind this puzzling statement attributed to the Buddha?--and why should we care?

I recently came across a fascinating article by the mathematician Fred Linton of Wesleyan University, which explains the Buddhist idea of the four possibilities in the verse above in a logical, mathematical way. Before getting to the math, let's look at some everyday examples that Linton provides for situations where the additional two logical possibilities may hold: both true and not true; and neither true nor not true. If you have a student, Linton writes, who is brilliant in mathematics but also has a knack for getting arrested in campus demonstrations, you might rightly say that he is both very bright and not very bright. A cup of coffee with just a small amount of sugar, Linton points out, could very well be described as neither sweet nor not sweet. Such examples abound.
Apparently, Eastern thinking is more in line with such gradations of truth and falsity, so that the law of the excluded middle doesn't quite apply. In a sense, the strict interpretation that anything must be either true or not true may well represent a Western bias in thinking about nature and life. In an e-mail message, Linton provided more examples, of the other kind, and which are obviously Western in their strict "either or" bias: "You are either with me or against me"; "If you're not part of the solution, you're part of the problem"; and: "Which will you have?--tea or coffee?" Then Linton added: "I blame Aristotle for that!"

In fact, our Western logic does go back to Aristotle, famous for logical deductive statements such as: "All men are mortal; Socrates is a man. Therefore, Socrates is mortal." Sure--but there are other kinds of logic as well, and they apply in various situations. Eastern thinking modes seem to be more accepting of these differing ways of thinking. But the question arises: Isn't it true that mathematics brings us naturally to the Western "either or" kind of logic? Surprisingly, the real answer is: Not necessarily!
From Greece of the time of Aristotle (the fourth century B.C.), let's jump to the middle of the twentieth century, and find ourselves in Paris. Alexander Grothendieck (born in 1928), one of the brightest and yet most troubled mathematicians of all time (he is currently living in hiding in the French Pyrenees, having completely withdrawn from society believing that the Devil rules the world--See Pierre Cartier, "A Mad Day's Work," Bulletin of the American Mathematical Society 38, No. 4, 2001, p. 393) is recasting the entire field of algebraic geometry, and as part of that brilliant undertaking he invents a new concept: the topos. A topos means "location," or "place"--the plural, since this is a Greek word, is topoi; but in English we often also call them "toposes"--and it is the ultimate generalization of the concept of space.

Only Grothendieck could have the audacity, and the incredible facility with mathematics, to dare propose such a bold idea. Then, according to Cartier, "Grothendieck claimed the right to transcribe mathematics into any topos whatever." (Cartier, op. cit., p. 395; italics in the original.) Grothendieck, followed by William Lawvere and Miles Tierney, used category theory (an extremely general and abstract branch of mathematics championed by Saunders MacLane and Samuel Eilenberg) to recast mathematics into a new and far more supple mold. What did they do?
The problem with our Western, Aristotelian logic--which leaves no room between "true" and "not true"--is its crucial reliance on set theory. In set theory, which is often seen as the foundation of mathematics (surely you've heard everything about ZFC--Zermelo and Fraenkel's system; Cantor, Russell, and Gödel), a point is either a member of a set, or not a member of the set: there is nothing in between. This set-theoretic logic leads to the familiar Boolean algebra, which rules the truth or falsity of everything: unions, intersections, negations, and implications of events--and it forms the basis for computer science.
But with its powers, also come its limitations: Set theory cannot handle the in-between, the no-man's-land between truth and non-truth, being and non-being: the natural fuzziness in so many of life's situations. What Grothendieck's work brought to the fore was that there are other kinds of mathematics. Set theory is not the only possible foundation for mathematics: Topoi provide other--equally valid, if not more so (because they may avoid the paradoxes of set theory)--foundations. The key idea is that in a topos, which is based on the very general theory of categories, there is no necessity for set membership. In category theory, instead of sets, and set membership (which is too restrictive), we have objects and mappings (often called simply "arrows") between objects. The objects are very general, and so are the mappings. We write: f: a --> b; an object a is mapped by the arrow (the mapping) f into the object b. The generality of this approach is stunning at first, but mathematicians get used to it. What this device achieves is that it replaces the set-membership idea with the arrow idea. You no longer view things internally (using set membership), but rather externally: by how something is mapped, or transformed, into something else. The theory is very deep, and extremely powerful. Category theory relies on diagrams of objects and arrows, and a key concept that teaches us about the underlying mathematics is whether a diagram commutes or not (is going from A to C directly the same as going from A to B and then to C?--if the diagram commutes, you get a mathematical identity: f = gh, for the corresponding mappings, the product identified as map composition; and this can be extended).
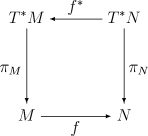
The topos was born within the context of category theory, but it has an additional, key property. A topos also has a topological structure. In topology, we study spaces and continuous functions. One important concept in topology is the idea of nearness. It turns out that this idea of a distance between a point and a set in topology can very nicely replace the idea of set membership (it's important to note, however, that the category of sets is also a topos--but there are others, and they provide the freedom we need from set membership).

So instead of the "true or false" structure derived from set theory, we can construct topoi in which this idea is mathematically replaced by a particular topological distance function, which allows for situations such as "both true and false" or "neither true nor false." It is, in fact, such a topos that Fred Linton exhibits in his paper mentioned above. Other topoi, with other kinds of generality and structure, are also possible. And all of them are mathematically valid! Before we move to physics, I want to recommend some books on category theory and topos theory. For categories, Saunders MacLane's book, Categories for the Working Mathematician, Springer, 1998, is the classic reference. For topoi, I highly recommend the very readable Topoi: The Categorial Analysis of Logic, by Robert Goldblatt, Dover, 1979.
So, unless you've never heard the expression "quantum weirdness"--in which case you must have come to this site by an unlikely accident of fate--you know by now why I am so enamored with topoi. But let's start with the simplest quantum idea: the Young double-slit experiment. You shoot a single photon at a barrier with two slits. What can the photon do? Go through slit 1, or go through slit 2, or go through both slit 1 and slit 2 (of course these depend on conditions we won't get into--but we all know this story; Richard Feynman called this "the only quantum mystery" since it embodies all the key elements). So you say that this covers the first three lines of the Buddha's choices according to Nagarjuna (in reference to one of the two slits): True, False, both True and False. But what about the fourth one: Neither True nor False? Well, so the Buddha didn't know everything--but at least he did get us away from our "it must be either true or false" hangup! But...hold it! If the photon has a high enough energy, it can turn into an electron-positron virtual pair. In this case, it would go through neither slit 1 nor slit 2. That Buddha was pretty smart after all!
So you'd think that topos theory should be pretty promising as a new foundation for quantum mechanics. Indeed, it is! And the great value that topoi add here is that they allow us to get away from the--artificial, in my view--reliance on probabilities (the Copenhagen interpretation), or even more outlandish interpretations of quantum weirdness: Many Worlds, or the de Broglie-Bohm approach, or anything else. We may find a topos that describes quantum logic directly from the mathematics (where the new topos--and Linton's is a good candidate--replaces the usual mathematical universe). We now have no need to resort to "collapsing the wave function" and then relying on the mysteriously appearing "probabilities," or on any of the other devices theoretical physicists use to describe quantum behavior.
It turns out that in 1997, the idea was discovered by Chris Isham of Imperial College, London, who wrote a key article about using topos theory in quantum mechanics (you can find it on arXiv). By 2011, several articles providing more detail about how topos theory could be used to explain quantum mechanics in a natural, mathematically-powerful way were published by Isham and his colleague Andreas Döring at Imperial College (all are on arXiv), so that a virtual revolution is now taking place in the foundations of physics. Why haven't you heard about it? The answer is probably: fashion. String theory, despite its setbacks, is still very sexy. People close to the media, such as Brian Greene, toot its horn--so the public hears much about it. And the recent Milner Fundamental Physics Prize ($3 million!) was awarded to several string theorists.
But recent work, by Chris Isham, C. Flori of the Perimeter Institute, and others, has begun to apply topos theory to quantum gravity--the realm in which string theory was supposed to do its magic--and this provides science with yet another outlet through which to pursue the Holy Grail of wedding quantum mechanics to Einstein's general theory of relativity. Because of the great power, generality, and versatility of topos theory, I vote for this mathematical theory as a likely candidate for producing the coveted "Theory of Everything."
I welcome your comments!






Comments