Two years ago, I expressed my doubts about the existence of a multiverse (or at least it's portrayal by some cosmologists) in a blog post in this forum. In the meantime, last March, the announcement about the discovery of gravitational waves got us perhaps closer to a multiverse--at least to one form of it, based on inflation. And then some problems with the Bicep data were discovered.
But the idea of a multiverse, once only a fantastic dream, has now still found its way into everyday conversation. Part of the reason is that cosmic inflation seems to imply the possibility of other universes, string theory's "extra dimensions" are another gateway to a multiplicity of worlds, and the very nature of quantum mechanics--at least in one of its interpretations--favors the possibility that our cosmos is not the only one around. 

As physicists have come to accept the scenario of a multiverse, despite the lack of any convincing evidence for its existence both from a verifiable theoretical framework and from any kind of confirmed experimental or observational results, this concept has already been taken to its limit: infinity. But infinity has always been the scourge of physics: Any kind of "infinite" answer to a calculation has always been taken as a sure sign that a theory had something very wrong with it. Lifetimes have been spent by theoretical physicists to correct such problems, that is, to "renormalize" theories so that the nonsensical infinite answers would disappear: QED and QCD being the most well known renormalizable theories. And while many kinds of physics calculations often make use of "potential infinity" through the infinitesimals of the calculus, no actual infinity has played a major role in the field. Not until now. 

The multiverse has almost invariably come to mean an actual infinite set of worlds. But what is its cardinality (or level of infinity)? The multiverse is necessary if one wants to try to explain the fine-tuning of the parameters of our universe using the anthropic principle, rather than resorting to some kind of creationism. The idea is that in a multiverse of the cardinality of the real line, there are member universes that correspond to any precise value for all the parameters (such as the fine structure constant, the strength of the dark energy, the ratio of the masses of the proton to the electron, the ratio of the strength of gravity to electromagnetism, and others) on a continuum of values. Then all you need to do is to invoke the anthropic principle and say that we live in that member of the (uncountably infinite) multiverse in which all the parameters are what they need to be to enable us to exist and observe them as what they are. 

But in fact, the continuum is very problematic when used to explain the multiverse. Brian Greene, David Deutsch, Max Tegmark, and other physicists have used the metaphor of the Infinity Hotel, or "Hilbert's Hotel," to argue for other universes and (at least in the case of Greene) the infinitely many copies of you and me running around in them, sometimes doing what we do in this universe and sometimes doing things slightly or completely differently. These arguments are all mathematically dependent on the so-called "Infinite Monkey Theorem." The idea is that a monkey randomly hitting the keys of a typewriter (the example is pre-computers, but a keyboard would do just fine) would type Hamlet, and all of Shakespeare, and all of the world's published works--if only given infinite time. What happens here is that the immense force of infinity dominates and, basically, given infinite time, anything that can happen, eventually will. Thus, the thinking goes, since for God (or any "higher power" or superior being) time is eternal, there must be infinitely many worlds with any kind of possibility happening in them. The problem is that physicists take this idea and run with it without, at times, a deep understanding of mathematical infinity.

To work infinity to solve for us the very difficult "fine tuning" problem, we need a continuous-type of infinity, and here the appropriate version of the Infinite Monkey Theorem fails. Let me explain this by proposing a new theorem.

Theorem (Aczel): 
With probability one, no set of monkeys, finite or infinite, forever typing numbers at random, will ever reproduce the number 

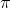
Proof: If you're good with measure theory, you could prove my theorem using a more-or-less straightforward application of the first Borel-Cantelli lemma. (While a proof of the usual "Infinite Monkey Theorem" makes use of the second Borel-Cantelli lemma.) But let me give you a cleverer and more instructive proof, which I've also devised, making direct use of mathematical analysis. We have:

Forget the beginning "3."--suppose that that's already written on the initial sheet the first monkey starts typing on. And assume that all monkeys use a uniform discrete distribution on the ten digits 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9, although this is not essential (and you can prove that if this is not true, and the distribution is different from uniform, the monkeys fail faster to get to ). 

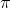In probability theory, we prove that a result is true "with probability one" (or "almost surely," which is analogous to "almost everywhere" in measure theory) by showing that it fails only on a set of arbitrarily small probability (measure). Arbitrary means: give me any small number you like, , and I will show you that I can make the error probability smaller than that number.

Suppose now that the monkeys perform their tasks successively. The first of the infinite (if it's finite, of course, they fail much faster) set of monkeys takes to the keyboard and strikes away, producing a random sequence of digits. I will now take the arbitrarily small you've given me and halve it. Now, the probability that Monkey 1 gets the first decimal of 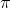 (which happens to be "1") is 1/10. The probability that the monkey gets the first two digits of pi correctly (the 1 and the 4) is (1/10)(1/10). And so on. Now, given the: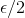

I can find a number (representing the decimal digits of 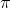 counted from the beginning), N₁, such that: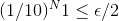 

At that point, Monkey 1 has failed with probability one. Monkey 2 now steps to the keyboard, and continues at the point N₁, where Monkey 1 has failed (I give my monkeys a break--not making them start from the beginning). I now halve my epsilon again, and through it I find N₂, defined such that:

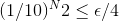
Continuing in this way, and assuming an infinite set of monkeys, who can type "forever" (meaning as long as necessary), the probability that they succeed is:

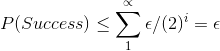
The right-hand equality follows from the sum of the infinite series (1/2)ⁱ    
This sum is equal to 1. This proves the theorem.

What does it all mean? It means that if you create universes that are countably infinite then, yes, you could say that things will happen (maybe something like you and me will materialize in other universes--maybe), similarly to how a monkey might reproduce Hamlet after a really, really long time. But you can't really say anything about parameters and fine tuning. If you think that you can somehow "create" finely-tuned parameters for your universe, ones that live on the continuum of numbers (such as pi!), then you can forget about it: With probability one (that is, except for on a set of measure zero), this will never happen! Put another way, there is a zero probability that you could ever recreate finely-tuned parameters that would replicate those of our universe. What does this imply about our own universe?

Front page image credit: istock.com