 1:1 In the beginning Newton declared space and time. 1:2 And space was without form, and void; and darkness was upon the face of the deep. 1:3 And Newton said, Let there be force: and there was force. 1:4 And Newton saw the force, that it was good: and Newton divided force from straight motion. 1:5 And Newton called force change of momentum, and straight motion he called momentum conservation. And the evening and the morning were the first day.
1:1 In the beginning Newton declared space and time. 1:2 And space was without form, and void; and darkness was upon the face of the deep. 1:3 And Newton said, Let there be force: and there was force. 1:4 And Newton saw the force, that it was good: and Newton divided force from straight motion. 1:5 And Newton called force change of momentum, and straight motion he called momentum conservation. And the evening and the morning were the first day.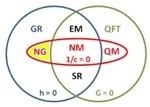 1:6 And Newton said, Let there be a force in the midst of matter, and let it divide matter from energy. 1:7 And Newton divided matter which were under influence of the force from energy which were above the force: and it was so. 1:8 And Newton called the force Gravity. And the evening and the morning were the second day.
1:6 And Newton said, Let there be a force in the midst of matter, and let it divide matter from energy. 1:7 And Newton divided matter which were under influence of the force from energy which were above the force: and it was so. 1:8 And Newton called the force Gravity. And the evening and the morning were the second day.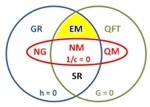 1:9 And Maxwell came and said, Let the matter under influence of gravity be gathered together unto one place, and let the vacuum appear: and it was so. 1:10 And Maxwell called vacuum the field; and the gathering together of matter called he Source: and Maxwell saw that it was good. 1:11 And Maxwell said, Let the field bring forth electricity, magnetism yielding north, and the waves yielding light, whose Source is in itself, upon the field: and it was so. 1:12 And the field brought forth electricity, and magnetism yielding North, and the waves yielding light, whose Source was in itself, and Maxwell saw that it was good. 1:13 And the evening and the morning were the third day.
1:9 And Maxwell came and said, Let the matter under influence of gravity be gathered together unto one place, and let the vacuum appear: and it was so. 1:10 And Maxwell called vacuum the field; and the gathering together of matter called he Source: and Maxwell saw that it was good. 1:11 And Maxwell said, Let the field bring forth electricity, magnetism yielding north, and the waves yielding light, whose Source is in itself, upon the field: and it was so. 1:12 And the field brought forth electricity, and magnetism yielding North, and the waves yielding light, whose Source was in itself, and Maxwell saw that it was good. 1:13 And the evening and the morning were the third day.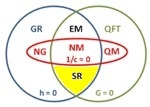 1:14 And Einstein came and said, Let there be movement between the light to divide absolute from relative; and let them define time: seasons, and days, and years. 1:15 And let them render space and time one: and it was so. 1:16 And Einstein created a principle; a single principle to rule the dynamics of matter and also to rule fields. 1:17 And Einstein applied it to the firmament of the heaven to cast light upon the doubters, 1:18 And to divide reality from the darkness of the ether: and Einstein saw that it was good. 1:19 And the evening and the morning were the fourth day.
1:14 And Einstein came and said, Let there be movement between the light to divide absolute from relative; and let them define time: seasons, and days, and years. 1:15 And let them render space and time one: and it was so. 1:16 And Einstein created a principle; a single principle to rule the dynamics of matter and also to rule fields. 1:17 And Einstein applied it to the firmament of the heaven to cast light upon the doubters, 1:18 And to divide reality from the darkness of the ether: and Einstein saw that it was good. 1:19 And the evening and the morning were the fourth day.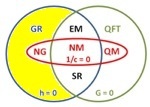 1:20 And Einstein said, Let matter and field bend space and time, and Let all movements maximize duration. 1:21 And the shape of space and time created gravity, and gravity moved the planets and bended light: and Einstein saw that it was good. 1:22 And Einstein blessed the unity of space and time. 1:23 And the evening and the morning were the fifth day.
1:20 And Einstein said, Let matter and field bend space and time, and Let all movements maximize duration. 1:21 And the shape of space and time created gravity, and gravity moved the planets and bended light: and Einstein saw that it was good. 1:22 And Einstein blessed the unity of space and time. 1:23 And the evening and the morning were the fifth day.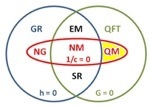 1:24 And Bohr and Heisenberg came, and they said, Let energy bring forth quanta: and it was so. 1:25 And Heisenberg and Bohr said, let there be quanta for the harmonic oscillator, and quanta for the hydrogen atom, and quanta for everything that creepeth upon the earth: and they saw that it was good.
1:24 And Bohr and Heisenberg came, and they said, Let energy bring forth quanta: and it was so. 1:25 And Heisenberg and Bohr said, let there be quanta for the harmonic oscillator, and quanta for the hydrogen atom, and quanta for everything that creepeth upon the earth: and they saw that it was good.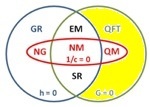 1:26 And Feynman and others came, and they said, let us make quantum fields: and let them have dominion over over every creeping particle that creepeth upon the earth. 1:27 So Feynman and others created quantum fields, bosonic and fermionic they created them. 1:28 And All blessed the quantum fields, and said unto these, Be fruitful, and multiply, and replenish the vacuum, and subdue it: and have dominion over reality.
1:26 And Feynman and others came, and they said, let us make quantum fields: and let them have dominion over over every creeping particle that creepeth upon the earth. 1:27 So Feynman and others created quantum fields, bosonic and fermionic they created them. 1:28 And All blessed the quantum fields, and said unto these, Be fruitful, and multiply, and replenish the vacuum, and subdue it: and have dominion over reality.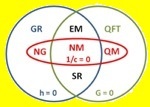 1:29 And All said, Behold, we rule the quantum field, which is upon the face of all the universe, and every piece of space and time, yet we fail to understand how the quantum bends space and time. 1:30 And it was so. 1:31 And All saw every quantum gravity theory that was made, and it was not good. And the evening and the morning were the sixth day. 2:1 Thus space and time refused to yield to the quantum. 2:2 And despite all their work they made; nobody found rest on the seventh day.
1:29 And All said, Behold, we rule the quantum field, which is upon the face of all the universe, and every piece of space and time, yet we fail to understand how the quantum bends space and time. 1:30 And it was so. 1:31 And All saw every quantum gravity theory that was made, and it was not good. And the evening and the morning were the sixth day. 2:1 Thus space and time refused to yield to the quantum. 2:2 And despite all their work they made; nobody found rest on the seventh day.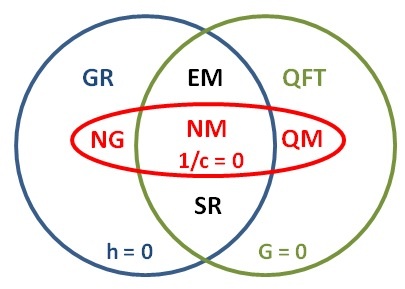
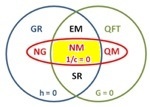
Centuries of fundamental physics condensed in a single Euler diagram. The various theories are grouped according to which aspects of reality are ignored. Red oval (1/c = 0, vanishing slowness of light): theories ignoring relativistic effects, blue circle (h = 0, vanishing quanta): theories ignoring quantum effects, green circle (G = 0, vanishing gravity): theories ignoring spacetime curvature.
Specific theories are labelled as follows:
NM: Newtonian mechanics (Isaac Newton, 1687)
NG: Newtonian gravity (Isaac Newton, 1687)
EM: Electro-magnetics (James Maxwell, 1862)
SR: special relativity (Albert Einstein, 1905)
GR: general relativity (Albert Einstein, 1916)
QM: quantum mechanics (Erwin Schrödinger, Werner Heisenberg, 1925)
QFT: quantum field theory (Sin-Itiro Tomonaga, Julian Schwinger, Richard Feynman, and Freeman Dyson, 1948)
Quantum gravity, the elusive theory of everything, is represented by the area external to the two circles.





Comments