The dull sound of the topic as stated above should not deceive you: this is a really exciting, interesting technology, which allows the measurement of physical quantities with high precision. Since the M in CMS stands for "muon", we certainly care for the precise measurement of muons -and muons are the particles used for the calibration procedure.
What happens when a charged particle leaves ionization deposits ("hits") in the silicon tracking system is that we can reconstruct its trajectory, forming a track. The track is curved in the plane transverse to the beam, because the S in "CMS" stands for "solenoid", a big cylinder that provides a B= 3.8 Tesla magnetic field within its volume. If you know what the Lorentz force is, you might also remember the formula P = 0.3 B R, expressing the proportionality of the momentum of a charged particle and its curvature in a magnetic field. This demands that within the CMS solenoid a P = 1.14 GeV muon follow a curved trajectory, which resembles a circle of radius R = 1 meter if observed in the "transverse" plane to the beam axis, the one along which the solenoid is symmetrical. By measuring the curvature, we determine the transverse momentum!
Things are always complicated if you want perfection. We of course can measure the position of the silicon hits with extreme accuracy, but alignment and positioning errors may create imperfections in the measurement of the track curvature. We also know the magnetic field with high accuracy, through Hall probes and other means, but imprecisions will affect the momentum measurement. Finally, the amount of material of which the tracking detector is composed affects the trajectory, producing further imprecisions if our map of the material is not perfect.
In the end, all the effects and all the details of the geometry of our detector are encoded in a carefully crafted simulation. With the simulation we can figure out what a 1-GeV track would look like, given our reconstruction and our assumptions about geometry, material, and magnetic field. But we need real data to verify that our model is correct, and to tune it in case it is not!
Real data: we now have it. CMS uses resonance decays to opposite-charge particles for this business: they are easy to identify, have little background, and there are plenty to play with. In particular, we use J/Psi meson decays to muon pairs for some of the checks of the momentum scale and resolution. Other dimuon resonances are also used -there is a large amount of such decays already available in the data so far collected- but here I will only discuss what CMS did with its J/Psi signal.
The dimuon mass spectrum in the vicinity of the nominal J/Psi mass value is shown in the picture below. A large number of signal events is observed. These events can be used to calibrate the momentum scale.
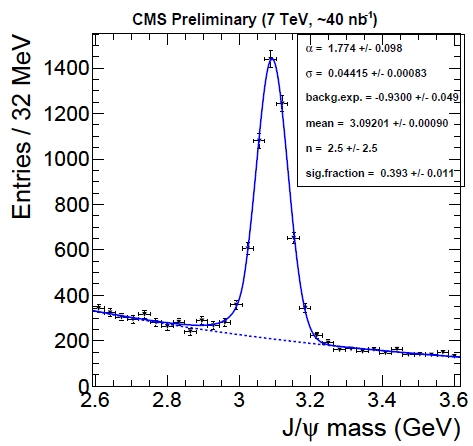
If one looks closely, one observes that the measured mass is very slightly lower than the nominal 3.097 GeV. This is already evidence for a very small underestimation of the momentum scale. To dig further, a simple thing one can do is to divide the J/Psi events depending on the value of the particle's reconstructed momentum or rapidity, measuring the mass in all sub-samples to check if in particular kinematical regions there is a bias. The bias, of course, would arise from the momentum reconstruction of the individual muons; but if one only measures the mass, which is a quantity constructed with the measurement of two muons, surely only an "average" bias can be detected, right ?
Wrong. Each muon from the decay of each J/Psi has a different momentum, travels through different parts of the detector, and is subjected to different reconstruction biases: we can turn these differences to our advantage. What we can do is to assume we know the functional form of these biases, and plug them into a likelihood function.
A further benefit with respect to methods I have seen in the past for the correction of scale biases is that a well-written likelihood function is also capable of extracting the momentum resolution from the same set of data. One just needs to produce a functional form (whose exact shape is suggested by simulation studies) that describes how the resolution on the momentum depends on the track kinematics; then, the likelihood fit will take care of finding the best parameters of the resolution function as well, by comparing the expected lineshape of the resonance with the mass value measured for each particle decay.
The likelihood is very complicated, because it accounts for the dependence of the mass on the muon momenta and the resolutions, and momenta and resolution in turn are functional forms of bias parameters. I know very well the code of this likelihood function, and I can tell you it is not for everybody! So I will abstain for once from finding a suitable analogy, lest I squeeze my brains for the rest of the evening. Let me just say that in the end, the likelihood maximization produces the most likely value of the parameters describing the bias functions, allowing a correction of the bias in the track momentum measurement!
Maybe it is best to show a couple of figures. The first one below shows the average mass of the J/Psi meson as a function of the pseudorapidity of the muons from its decay. The hatched red line shows the true value of the J/Psi mass; but more meaningful are the crosses, which show what should be measured with a perfect detector, given the fitting procedure (which, I am bound to specify, assumes that the lineshape follows a Crystal Ball form). The crosses are our "target": if we measure a mass in agreement with them, given our fitting procedure to extract the mass, our momentum scale is perfect.
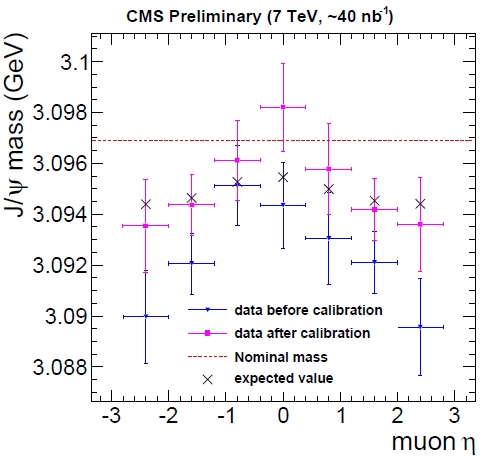
In blue you can see that the mass, before corrections, is biased low, especially at high rapidity. Instead, after the likelihood maximization and the correction procedure, we obtain the purple crosses. The agreement with the black crosses is still not perfect, and the statistics is too poor to detect further small deviations, but the demonstration of the validity of the procedure is clear!
And then, the resolution. This is also a function of rapidity in CMS, due to the way the detector is built and the decay geometry. The figure below shows what resolution we expected to measure as a function of rapidity, from simulated J/Psi decays (in black), given the measurement method.
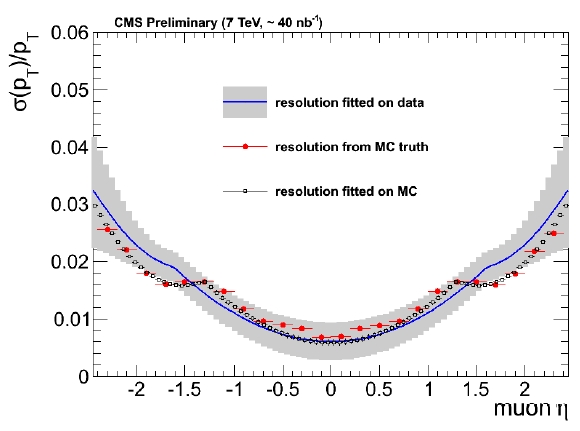
In red the figure also shows what the true resolution is, from simulated muons that are then compared to reconstructed ones. In blue, the band shows what instead CMS measured. The agreement between data and simulation is encouraging, and the result demonstrates the validity of the method. This functional form and its parameters are extracted from the way the reconstructed masses of J/Psi decays distribute around the nominal mass, accounting for the fact that muons in those events have different rapidity: the likelihood knows all the details, and produces a very complete answer to our question.
I think the method is very powerful and I cannot wait to see it applied to all resonances together, with more data -the different dimuon resonances have different kinematics and produce muons of widely varied momenta, allowing a very complete picture of the calibration and resolution of the CMS detector!




Comments