Ashay Dharwadkeris the founder and director of the Institute of Mathematics, Gurgaon, India.
He is interested in fundamental research in mathematics, particularly in algebra, topology, graph theory and their applications to computer science and high energy physics. Based upon the new proof of the four color theorem, he has developed a grand unified theory for the Standard Model and gravitation. In particular, this leads to a mathematically precise prediction of the Higgs boson mass.
Vladimir Khachatryan is a member of the Institute of Mathematics, Gurgaon, India and a PhD student at the Department of Physics and Astronomy, State University of New York, Stony Brook, USA. With an academic background in astrophysics, he currently works in the field of high energy nuclear theory, in an attempt to explain the experimental data revealed at RHIC and LHC. He is also interested in particle physics, especially in problems related to the Standard Model and beyond. In this guest post, Vladimir explains the reasoning behind the theory Ashay and him have developed. Beware: the mathematics is not for everybody; still, I believe this article was well worth the attention of the more knowledgeable among you here...We show that the mathematical proof of the famous four color theorem yields a perfect interpretation of the Standard Model of particle physics. One of the main applications of the proof is that we are able to calculate and predict the mass of the Standard Model Higgs Boson as described by Veltman and 't Hooft. The Higgs boson mass turns out to be MH0~ 126 GeV (A. Dharwadker and V. Khachatryan, Higgs Boson Mass predicted by the Four Color Theorem (2009), arXiv:0912.5189 [gen-ph] ). Let us describe the way in which we obtained this remarkable result, which is likely to be verified experimentally with the discovery the Higgs Boson at Tevatron and/or LHC in the near future, given the recent promising developments. The current experimental constraint on the existence of the Higgs boson is found to be in the energy realm from ~ 114 to 160 GeV. There is also a small possibility of its existence in the 170-185 GeV range, nevertheless, the lower energies are far more probable. In this brief note, we will not go into the complicated mathematical structure of our approach, instead we will attempt to show only the main steps which brought us to the conclusion that MH0 should be about 126 GeV.
The four color theorem arises as a fundamental problem in topology when the surface of a sphere or plane is partitioned into finitely many contiguous regions called a map. Two regions in the map are considered adjacent if they share a whole segment of their boundaries in common. The theorem states that the regions of any such map can always be colored by using at most four different colors, so that no two adjacent regions have the same color. It can be stated formally as follows:
For any subdivision of the plane or the surface of a sphere into finitely many non-overlapping regions, it is always possible to mark each of the regions with one of the colors 0, 1, 2, 3 in such a way that no two adjacent regions receive the same color.
The theorem was first conjectured by Möbius in 1840, later by DeMorgan and the Guthrie brothers in 1852, and by Cayley again in 1878. It remained one of the most celebrated and long outstanding conjectures in mathematics after many mathematicians tried to prove it for over a century. The conjecture was finally verified, using an extensive computer search for potential
counter-examples by Appel and Haken in the 1970's. However, this computer verification cannot be checked by humans, even in principle. In 2000, the theorem was proved mathematically by Dharwadker using algebraic and topological methods. It is a standard mathematical proof and can be verified by hand (A. Dharwadker, A New Proof of the Four Colour Theorem (2000), http://www.dharwadker.org/). That mathematical proof of the four color theorem has a rich topological and algebraic structure and its most important and fundamental application is a physical interpretation of the proof which directly implies the existence of the Standard Model of elementary particles (A. Dharwadker, Grand Unification of the Standard Model with Quantum Gravity (2008), http://www.dharwadker.org/standard_model/) .
The steps of the proof enable us to construct a specific type of Riemann surface (which is a mathematical construction based on the complex plane) and particle frame which forms the gauge. Then on this basis it is possible to specify well-defined rules in order to match the Standard Model in a one-to-one correspondence with the topological and algebraic structure of the particle frame. This correspondence is exact - it only allows the particles and force fields to have the observable properties of the Standard Model, giving us a Grand Unified Theory.
In order to exhibit how we obtain the one-to-one correspondence of the particle frame with the Standard Model, we start from the fact that the quantum-mechanical behavior of a free particle is completely described by its wave function, which is a solution of the relativistic Schrödinger wave equation. We show initially that this wave equation is sufficient to describe all the particles of the Standard Model on the particle frame. At each point (x, y, z, t) of space-time, the value of the wave function corresponds to a point on the boundary of a disc D centered at the origin of the complex plane C. The disc D may be oriented in two ways, clockwise or counter-clockwise depending on whether we select the normal vector according to the right-hand or left-hand rule. We call D a Schrödinger disc. According to the proof of the four color theorem, we select a specific map m(4) inside the disc. The regions of the map are partitioned into four equivalence classes that form the cyclic group {0, 1, 2, 3} under addition modulo 4, according to the color 0 (blue), 1 (yellow), 2 (green) or 3 (red) each region receives. In figure 1 below we show the map m(4) inside the Schrödinger disc D.
We now construct the Riemann surface which consists of 24 copies of oriented Schrödinger discs containing the map m(4) as shown below in figure 2. This Riemann surface is orientable since every orientation of a disc is carried over to the disc next to it.
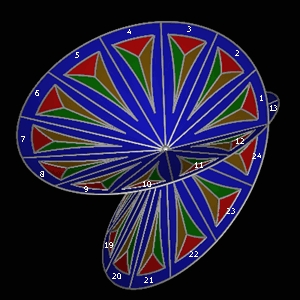
We define all the particles of the Standard Model by selecting certain regions (or their topological intersections) on this Riemann surface, in which context it is called a particle frame. Particle frames associated with space-time points constitute a vector bundle in mathematical terminology, and a section of the vector bundle, i.e. a particle frame at a space-time point, is called a gauge in the physics terminology. Thus, physical symmetries associated with sets of particles defined on a particle frame correspond to gauge transformations. The particle frame provides the general mathematical framework from which all the particles of the Standard Model will be defined, together with their basic physical properties: spin, charge and mass. Here we wish to describe our rules for matching the Standard Model in a one-to-one correspondence with the topological and algebraic structure of the particle frame.
- The Fermion Selection Rule. Distinct particle frames with fermions defined on them cannot be superposed at a point in space-time because of the Pauli exclusion principle. A fermion-type particle will be selected from the particle frame as follows. First select a disc out of the 24 discs and then select a region of the map on that selected disc. In this way,
there are two types of fermions and each type comes in three generations. Each generation consists of one lepton doublet and one quark doublet, as in the Standard Model. - The Boson Selection Rule. Many distinct particle frames with bosons defined on them can be superposed at a point in space-time, since the Pauli exclusion principle does not apply to the bosons. A boson-type particle will be selected from the particle frame as follows. First select a pair of fermion-type particles from the 24 discs (with selected regions of the
same color respectively) such that the two discs have an intersecting boundary (a ray on the particle frame). Then select another pair of fermion-type particles with selected regions of the same color as before, however, in such a way that the corresponding ray on the particle frame is distinct. Thus, we may select the boson-type particle by choosing a pair of rays on the particle frame with a particular color. In particular, two pairs of fermion-type particles that define a boson are interpreted as creation and annihilation operators during interactions in which the boson is exchanged. - The Higgs Selection Rule. A Higgs-type particle is a scalar boson, i.e., it does not select a preferred direction in space like a vector boson. It is selected as the intersection of all 24 discs of the particle frame. This is the central point in our construction of the Riemann surface, and this selection of the Higgs-type particle is unique. The origins of the
upper and lower sheets of the Riemann surface are interpreted as forming a Cooper pair and the Higgs particle undergoes Bose condensation, plunging into the lowest energy state possible. - The Spin Rule. The particle frame consists of four half-surfaces: the upper half of the upper sheet; the lower half of the upper sheet; the upper half of the lower sheet; the lower half of the lower sheet. Given a particle as a selection S of the intersection of a set of discs or as a pair of rays, count the number n of half-surfaces of the particle frame that intersect with a whole segment of S. Define s = n/2 to be the spin of a particle. We use this rule to explicitly calculate the spin of all the fermions and bosons on the particle frame.
- The Electric Charge Rule. We first associate each color with a unique absolute value of the electric charge according to the scheme: 0 (blue) → 0, 1 (yellow) → 1/3, 2 (green) → 2/3 and 3 (red) → 1. The labeling scheme for the signs has the following representation: the upper half of the upper sheet has a + sign; the lower half of the upper sheet has a - sign; the upper half of the lower sheet has a - sign; the lower half of the lower sheet has a + sign. Given a particle as a selection S of the intersection of a set of discs or of a pair of rays, assign a signed electric charge to a particle according to this scheme. This is defined to be the electric charge of the particle. We use this rule to calculate the electric charge of all the fermions and bosons on the particle frame.
The other rules may be briefly mentioned here: the weak isospin rule, the strong (color) charge rule, the mass rule, the equivalence rule, the antiparticle rule, the helicity rule and the CP transformation rule. We stress the importance of the mass rule by means of which we assign the
rest mass of each particle of the Standard Model matched onto the particle frame. Finally, incorporating all the above rules we have:
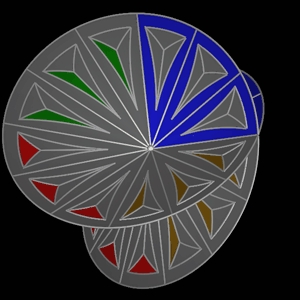
- The Standard Model Completion Rule. If all the particle frames corresponding to all particles in the universe were to be superimposed (hypothetically, of course) then the fermions and bosons should fit together perfectly according to the above rules, forming the complete Standard Model on the particle frame. The discs 1, ..., 24 of the particle frame represent the Schrödinger discs of the 24 distinct spin 1/2 fermions νe, νμ, ντ, t, c, u,
e, μ, τ, b, s, d, νe, νμ, ντ, t, c, u, e, μ, τ, b, s, d in the Standard Model, respecting all the above rules as shown in figure 3(a) below. There cannot be any other fermions in our mathematical construction of the Standard Model. Also, each of the 24 pairs of rays of the particle frame represent four Schrödinger discs of a unique boson in the Standard Model: the photon γ (spin 1), the three vector bosons W+, W-, Z0 (spin 1), the gluon AS (spin 1) and the graviton g (spin 2), respecting all the above rules as shown in the figure 3(b)
below. The branch point in the center of the particle frame represents the Higgs boson H0 (spin 0). There cannot be any other bosons in our mathematical construction of the Standard Model.
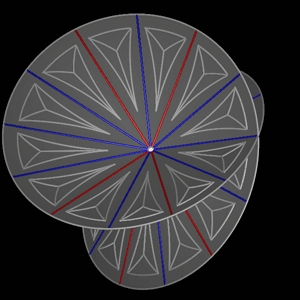
We briefly note that it is also possible to obtain the values of the Weinberg and Cabibbo angles on the particle frame. The Weinberg angle ΘW is a parameter that gives a relationship between the masses of the W+, W-, Z0 bosons as well as the ratio of the weak Z0 mediated interaction, called its mixing. In our model, the components of the weak Z0 field mix with the components of the weak W+, W- fields and the angle subtended by the mixing Schrödinger discs on the particle frame is exactly π/6 radians or 30 degrees, as shown in figure 4 below.
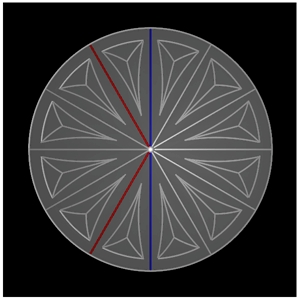
Hence, ΘW = 30 degrees on the particle frame. This is in good agreement with the SLAC experiment, which estimates sin2ΘW = 0.2397, i.e. ΘW = 29.3137 degrees (this is a "running" value, depending on the momentum at which it is measured, with a significance of 6 standard deviations). The Weinberg angle is a measure of the strength of the weak force on the particle frame. For the Cabibbo angle we calculate the value θC = (4/9)ΘW ~ 13.33 degrees, which is proportional to the strength of the weak force on the particle frame.
Finally, we show how the mass of the Standard Model Higgs Boson H0 can be calculated on the particle frame by using the above rules. By the Higgs Selection Rule, the Higgs particle is given as the intersection of all 24 discs of the particle frame. We may regard the Higgs particle asthe intersection of the discs 1,...,12 of the upper sheet (the origin of the upper sheet), and the Higgs antiparticle as the intersection of the discs 13,...,24 of the lower sheet (the origin of the lower sheet). However, the Higgs particle and antiparticle are identified as the branch point
of the Riemann surface. These 24 discs together represent the Schrödinger discs corresponding to the Higgs field and the blue branch point at the center represents the Higgs particle on the particle frame as shown below in figure 5.
Thus, by the Higgs Selection Rule, the Higgs particle is a scalar boson. Furthermore, by the Spin Rule, the spin of the Higgs boson is 0; by the Electric Charge Rule, its electric charge is 0, by the Weak Isospin Rule, its weak isospin is 0; and by the Strong Charge Rule, its strong charge
is neutral with Nc = 1.
The Higgs boson has not been observed yet but it is an inevitable consequence of the Higgs-Kibble mechanism, whereby it attributes mass to all particles of the Standard Model, including itself. The Higgs Selection Rule and the Mass Rule give the following mechanism for obtaining the mass value of H0. Since the Higgs particle/antiparticle will be identified (as a Cooper pair), their combined mass would then be the sum of the masses of all the bosons defined on the particle frame. However, note that only the rest masses of the three gauge vector bosons W+, W- and Z0 contribute to the sum because all the other bosons are massless. Thus, we can have all types of bosons superposed on a single particle frame, and the single Cooper pair of the Higgs particle/antiparticle must be able to attribute energy/rest mass to all types of bosons on this particle frame, by the Higgs-Kibble mechanism.
The particle frames of the bosons can be superposed at a point in space-time because they follow the Bose-Einstein statistics. Hence, this Cooper pair must have at least enough energy to attribute the sum of the rest masses of all types of bosons defined on the particle frame. On the other hand, the most important property of Bose condensation is that the Cooper pair of the Higgs particle/antiparticle must have minimum energy, so it can have at most the energy required to attribute the sum of the rest masses of all types of bosons defined on the particle frame. This must be the lowest energy state possible for the Higgs boson when it undergoes Bose condensation. Summarizing all these facts, we obtain the formula for the Higgs boson mass defined on the particle frame as follows:
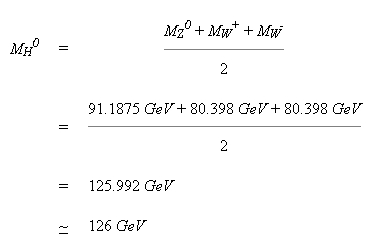
The Higgs boson mass value MH0 ~ 126 GeV results from the currently best known experimental mass values of the three gauge vector bosons from the Particle Data Group. In conclusion, we would like to emphasize that we have calculated the mass of the Higgs boson from the above formula by taking into account the whole topological and algebraic structure of the Riemann surface, the particle frame and the proof of the four color theorem.
Comments