The result is not groundbreaking, in the sense that as expected no signal is observed in the DZERO data. [The LHCb collaboration at CERN has obtained a first evidence of this process last November, as discussed in this other article]. The collaboration can only set an upper limit on the branching fraction B(B_s -> μμ), which is a quantity of great interest: it is a tiny number in the standard model (3.5 billionths), and it could be modified significantly by the existence of new particles, for example supersymmetric ones.
This is a striking example of the interest of measuring quantities that are predicted to be very small or zero by the existing theories: when a process has zero expected rate according to a given theory (the standard model in our case), observing it even once is already a proof of the failure of the theory. However, due to the huge number of collisions that have been collected at the Tevatron since 2002, even these quite rare processes can in principle produce an observable signal. Not to mention that backgrounds, even quite improbable ones, become significant when the statistics is so large.
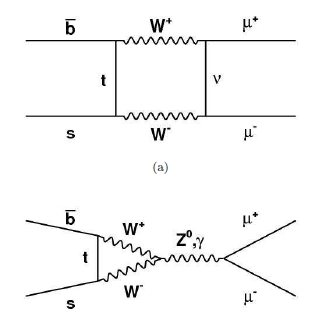The reason why this branching fraction is so sensitive to the existence of massive new particles is that it is a "loop process". In quantum field theory language, this means that the decay can only occur through diagrams containing closed loops of particle lines, such as those shown on the right (those shown are in fact the simplest diagrams by means of which the B_s meson - coming in from the left in the diagrams, and made up by a b-quark line and a s-quark line- can produce a dimuon pair in the decay). Now, inside a quantum loop one has to consider that ANY existing particle can play a role. And each new particle one hypothesize will modify the probability that the decay occurs, making it more or less likely. Yes, a dampening of the observed rate can also be due to a new particle, in case interference effects take place. In any case, I think you now understand why measuring the branching fraction of this rare process and comparing it to standard model calculations is a good idea.In practice, the DZERO folks analyze events with two well-reconstructed muons of opposite charge, and then construct a multi-dimensional discriminant using the observed kinematics. This allows a very powerful background reduction, such that at the end of the day they expect to observe only an average of 4.3 background events in their data, in the "signal window", a small region of invariant mass of the two muons which corresponds to the mass of the B_s meson, a particle composed of a b-quark and a s-quark.
The expected amount of signal that DZERO computes according to standard model predictions in the signal region is of 1.3 events: this means that the search is not sensitive enough to observe the signal, unfortunately; but the number of events accepted by the full selection in the signal window may still tell whether the signal process has contributed in an anormally high way.
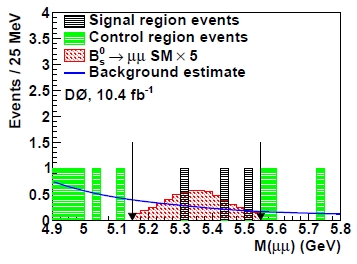The search, as is common practice in cases where a small number of events in the signal region may change the result, is performed blindly: DZERO optimizes the value of the multidimensional discriminant and defines search window and background expectation before actually looking at how many events fall in the net. In the end, they observe three events in the search window delimited by the two black arrows (see figure, right): these three events are in good agreement with the expected background of 4.3 (the expected distribution of backgrounds is shown by the blue line), but they also agree with the hypothesis that a standard model signal is also present (the red histogram, which however has been inflated by a factor of five for display purposes), contributing an average of 1.3 events. In other words, the three captured events may be all background, all signal, or a combination of the two processes, and their number is compatible with both the "null hypothesis" that there is NO standard model decay of the B_s in dimuons (zero signal) and with the "alternate hypothesis" that the signal exists with the expected rate.So is the search totally inconclusive ? Of course not. What the data do tell is that they are incompatible with a signal branching fraction five times larger than what the standard model predicts, for instance. Using Poisson statistics, in fact, one can calculate how frequently one should observe as few as three events when the expected value is larger. Let us review this simple calculation to put to focus the idea.
The Poisson distribution has the formula
f(N;μ) = [exp(-μ)*μ^N)]/N!
where exp() is the exponential function, and N! denotes the factorial (N!=N*(N-1)*...*2*1).
This means that if one expects an average μ, the probability to observe exactly N events is f(Ν;μ). Now let us then compute what is the probability to observe three OR FEWER events if the average is 4.3, i.e. if there is NO standard model signal. This is given by
P(N<=3; No SM signal) = f(0;4.3)+f(1;4.3)+f(2;4.3)+f(3;4.3)
and with a computer you can evaluate it to be
P(N<=3; No SM signal) = 0.0136 + 0.0583 + 0.1254 + 0.1798 = 0.3772.
So the observation is perfectly consistent with the background-only hypothesis: it occurs 37.7% of the time under the specified conditions. If, on the other hand, one supposes that the SM signal is also there, one needs to substitute μ=4.3+1.3 =5.6 in the formula. This causes P to become
P(N<=3; true SM signal) = 0.0037 + 0.0207 + 0.0580 + 0.1082 = 0.1906.
Can we exclude that the branching ratio of the B_s is as predicted from the standard model ? Of course not - there is a 19% chance to see as few events as we have in that case. However, we can then ask a different question: what is the largest amount of signal, in addition to the 4.3 background events, that would make our observation have a probability of 5% to occur ? This equates to computing the "95% confidence level" on the signal size, given the observed three events. You can write a simple computer program to perform the calculation; I did, and the result is that the signal needs to be smaller than 3.5 events, or the total of signal and background smaller than 7.8, in order for us to have a 5% or better chance to observe as few as three events.
Using the detector acceptance to the signal and other normalization factors (crucially, the number of detected B_s mesons in a much more frequent decay mode), DZERO can turn that number into a limit of the branching fraction to dimuons, at 15 billionths. Note, however, that in the above calculation I have completely ignored, for simplicity in the discussion, the uncertainty on the background prediction. In reality, DZERO estimates the background at 4.3 +-1.6 events. This boils down to a modification of the simple calculation above, to account for the probability density function of the background expectation. The result is thus a bit different from the cited 3.5 events - a larger maximum number of signal is allowed, given the uncertainty. But the final result is the one I quoted: the ratio is limited to be smaller than 15 billionths.
What does the result imply for the existing searches of the rare B_s decay mode ? Not much, as the DZERO paper itself admits. LHCb has already observed some first hints of a signal, and also ATLAS and CMS are much more sensitive than the present DZERO search, having limited the ratio to smaller values already with summer 2012 results. Now, in fact, the CERN experiments are competing to be the first to observe the signal conclusively, rather than to set the smaller upper limit on the signal cross section.
One thing, however, needs to be stressed. It is very nice to see DZERO publishing a result using the full statistics it collected in 10 years of data taking. These analyses take time, and at the Tevatron the event reconstruction, reprocessing, and calibration is a more lengthy process than at the CERN experiments. One could imagine that results based on the full statistics at the Tevatron would need to wait for more time. Instead, people there are trying to finish the job with discipline, regardless of how significant are the resulting measurements. This is a quite important activity, which justifies the requests to extend the lifetime of Tevatron running that allowed to continue data taking until two years ago.
Comments