Natural width -the width of the resonance shape peaking at the rest mass of the particle- is a fundamental attribute of elementary particles, and arguably an even more important one than the mass itself. In fact the width determines the lifetime of the particle: particles that live longer have a smaller width because they have more time to "settle" to their nominal rest mass. In the case of the Higgs, if we found out that its width is substantially larger than what the standard model predicts, we would immediately know that there are possible decay modes of which we know nothing about yet: it would be a clear indication of new physics. The presence of extra ways for the particle to decay in fact ensures that the lifetime will be shorter, and the width larger.
4.15 MeV are a really small number as compared to the experimental resolution in the particle mass which we may achieve with the CMS or ATLAS experiment. Hence there is no chance to measure that parameter directly: any Higgs mass distribution experimentally determined at the LHC will have a observed width waaaay larger than the natural one. However, we can measure the Higgs natural width indirectly by looking at very off-shell Higgs bosons.
It has in fact been noted by several theorists that the peculiar production processes yielding Higgs bosons at the LHC modify significantly the observable Higgs boson lineshape. In other words, what we can detect at the LHC in a histogram of the Higgs mass is the convolution of the Lorenzian shape - a peak with a width equal to the natural width of the Higgs, centered at the Higgs mass - with the production cross section, which receives enhancements at high mass due to the large coupling of the Higgs boson with the heavy top quark. The result is that instead of quickly dying out, the expected signal mass distribution has a significant tail at very high masses.
It looks strange to think that a 125 GeV Higgs boson may yield a significant signal at masses of 300 GeV and more, but that is exactly what happens. What is most interesting, however, is that the strength of the signal there is strongly dependent on the natural Higgs width. Check out for instance the picture below, which shows the reconstructed mass of ZZ pairs by CMS. A Higgs boson with a width of 25 times the SM prediction (i.e. just a bit more than 100 MeV or so) would produce a very significant enhancement!
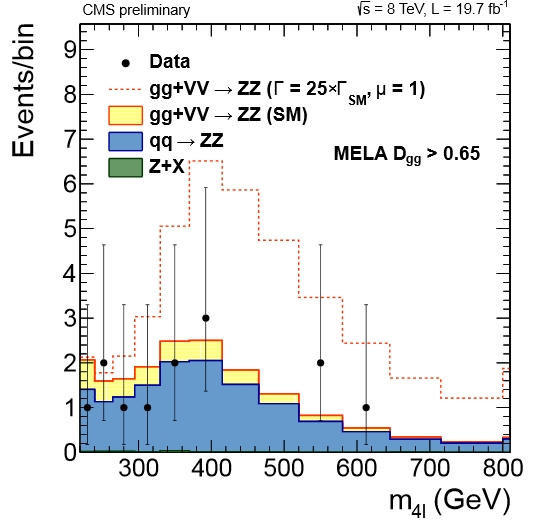
Above, the four-lepton mass distribution of CMS data collected in 2012 8-TeV pp collisions is compared to ZZ background (blue) and SM prediction (in beige), and with a Higgs with a natural width 25 times the SM prediction (dashed histogram).
By studying both the 4-lepton final state of ZZ events and the two charged leptons + 2 neutrino final state, CMS has managed to determine an upper limit on the Higgs width at 4.2 times the standard model value, at 95% confidence level. That is already cutting into several models that could predict much larger widths by hypothesizing the existence of unknown decays. Note that results are extracted for two cases: under the assumption that the global production rate is what the SM predicts, and under no assumption on the rate. A larger global production would enhance the tails, but production rates much larger than the SM prediction are however excluded by looking at the 125 GeV peak. The x4.2 times limit is extracted under no rate assumption.





Comments