A weekly visit to the Cornell Arxiv is more than enough for a physicist like me, since my daily work is not affected too much by whatever happens to be published there. Oftentimes, when I browse the contents of hep-ph (the folder containing preprints on particle phenomenology) I do not end up actually reading any papers, and limit myself to "sniffing" what is going on, by looking at the titles and author names. But at times I venture to browse through the pages, with mixed results.

Today my attention was caught by a triad of papers casually listed one after the other: written by different authors, but all on topics closely connected to an issue that these days a particle physicist cannot avoid paying attention to: one which presently constitutes the largest deviation of experimental measurements from standard model predictions. I am talking about the so-called "anomalous magnetic moment of the muon", the quantity called , which is currently lying 3.1 standard deviations above theoretical predictions: theory predicts

, while experiments measure .


Some very basic introductory facts about the magnetic moment

Perhaps a couple of words on the anomalous magnetic moment of the muon are in order, before I venture to summarize the contents of those three papers.

Muons, as all other charged Dirac particles, are endowed with a property, called magnetic moment. Classically, this can be understood by the fact that these particle have an intrinsic spin as well as an electric charge, and any rotating electric charge generates a magnetic field. In quantum mechanics, the corresponding magnetic moment is subjected to small quantistic corrections due to loop effects -the emission and reabsorption of virtual particles. This, in fact, is the most classic example of a quantum anomaly -the failure of classical laws to extrapolate down to the quantum level.

The precise measurement of the deviation of the magnetic moment of an elementary particle from its classical value provides access to a precise verification of the structure of the theory: since this is a loop effect -that is, one produced by the exchange of virtual particles- any new particle contributing to these quantum loops would produce a deviation of the measured value from the standard model prediction, given that the standard model does not include that particle in the calculation.

However, it must be said that the precise computation of the standard model prediction is very complicated: electromagnetism, weak interactions, and strong interactions all have to be taken in account with the utmost precision. Nowadays, the largest uncertainty in the calculation of the anomalous magnetic moment of the muon comes from quantum chromodynamical effects, which cannot be computed as precisely as electroweak effects (since QCD is not as manageable at low energy as are other interactions), and must therefore be extrapolated from other processes, like low-energy electron-positron annihilations producing pions, or hadronic tau lepton decays.

As quick-and-dirty this introduction is, my idea of this afternoon was describing papers rather than basic physics, so please let me now go back to the articles!

Three Articles on g-2

This funny concentration of papers on the muon g-2 stimulated me to have a closer look. So here is a summary of their contents. Beware, my understanding of the topic is quite limited, so if you are interested in the details you should follow the links to the papers themselves... Otherwise, my summary might just be all you need.

hep-ph 1001-3696, titled "Electron and Muon g-2 Contributions from the T' Higgs Sector", is a study of the experimental constraints to the T' model, coming from g-2 measurements. The T' model relates quarks and electrons through a group of symmetry called the tetrahedral T' group. This fancy construction appears to have some value in that it may be used to predict the phenomenology of neutrino mixing. Since in the model electrons and muons have different couplings to the corresponding Higgs fields, one may use the observed values of g-2 measurement of electrons and muons to derive some information on the model parameters.

The authors show that the muon g-2 discrepancy can be accommodated well in the T' model. After a few pages of calculations, they conclude that

"Given the Higgs mass bound from LEP, the upper bound on the electron Yukawa coupling consistent with the perturbation theory would be allowed. [...] Assuming that the LEP bound also applies to the mass of the Higgs that directly couples to muon (there is a triplet of Higgs fields coupling to the three kinds of fermions in this model, NDR), we found that the Yukawa couping should be much larger than the corresponding standard model value in order to explain the discrepancy."

hep-ph/1001.3703, titled "Recent progress on isospin breaking corrections and their impact on the muon g-2 value", was listed just below the previous paper in hep-ph this morning. The author, G. Lopez Castro, describes some recent results that are capable of bringing in better agreement the dominant contributions from QCD effects to the muon g-2 anomaly when they are estimated with pion pair production in electron-positron annihilation or with tau decays data. Both methods seek to evaluate how much a virtual photon "fluctuates" into hadrons -a quantum correction directly affecting the muon anomaly.

The paper sounds very interesting, but it is very technical and I feel totally unqualified to discuss it in detail, so let me just quote from the conclusions:

The new isospin-breaking corrections get closer the results of based on e+e- and tau lepton data. These corrections also affect the prediction of the branching fraction obtained from electron-positron data via the isospin symmetry. [...] It is very appealing that the new isospin-breaking corrections reduce simultaneously the different manifestations of the so-called e+e- vs tau lepton discrepancy.

Finally, hep-ph/1001.3704, titled "Tenth-order lepton g-2: Contribution from diagrams containing sixth-order light-by-light-scattering subdiagram internally" (what a ugly title!) discusses the calculation of some very tiny but still important corrections to one of the electromagnetic contributions to the anomalous magnetic moment of all lepton species (electrons, muons, and tau alike).
The authors note in the introduction the well-known fact that the measurement of the anomalous magnetic moment of the electron has given us the most stringent test of quantum electrodynamics: the experimental value of the electron anomaly is known to within a few parts in a trillionth. To match such astounding precision, theoretical calculations must include high-order loop effects. In particular, the quantum electrodynamical corrections have so far been computed up to eight-order (we will see what this means in diagrammatic form below). They decided to go to tenth-order, computing 12,672 additional Feynman diagrams not previously considered. Some of these are shown in the figure below:



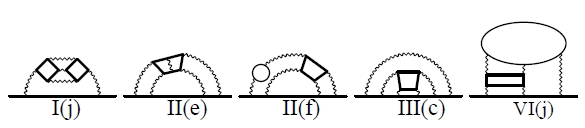
As you see, the thing that these diagrams have in common is that they all contain exactly ten vertices -points where the wiggly photon lines meet the continuous fermion lines. This is what we mean when we say "tenth-order": to each vertex you must associate a factor in the calculation of the amplitude, and since alpha_em is less than one hundredth, the result is a really small correction to the propagation of the original electron (the horizontal line).

And the conclusions ? Well, they are there, but they look slightly obscure to me. I would have liked a summary which allowed one to verify whether progress has been made in reconciling the muon anomaly measurement with the theoretical prediction. Hopefully we will soon see some update -albeit probably small- on the discrepancy in the muon anomaly, based on the results of this calculation as well as the results of the previous paper.

The question is then, do you want those 3.1 standard deviations to grow to five, or go down to zero ? I of course would love to see the discrepancy increase, but I am putting my money on the other result...