For instance, the rotational velocity of stars around spiral galaxies does not decrease with their distance from the center as it would if what they were orbiting were only the luminous matter in the galaxy. Different but consistent evidence on the presence of DM in elliptical galaxies also exists, and is based on the dispersion in the velocity distribution of stars. On a larger scale, effects of DM appear in the comparison of the mass of galaxy clusters computed with different observational data.
As an Ockhamist by nature, I refrain from accepting the existence of uncalled-for new entities unless these are "economical" - their existence must reduce instead than increase the oddity of the matter under consideration. But indeed, I have come to believe that dark matter does exist because DM is an economical, although mindboggling, explanation.
In the past two decades years the evidence of DM in the universe also became one of the strongest drivers for those who were enticed by the melodious sound of Supersymmetric sirens. For those of you who haven't come cross with it yet, Supersymmetry (SUSY) is a bold theory that predicts the existence of a supersymmetric copy of each subnuclear particle we know. It does so in the attempt to "mend" a notable shortcoming of the currently accepted theory of subnuclear physics (the Standard Model, SM), its "naturalness" (I won't discuss naturalness here, see elsewhere).
Now, a "cosmic coincidence" was noted by cosmologists some time ago: if SUSY particles exist, there must be one among them which is the lightest (doh). If this is neutral and cannot decay into SM particles, then however many copies of it have been produced in the Big Bang must still be around today. Like lonely ghosts, these particles (called "neutralinos") would gravitate around galaxies as luminous SM matter does. Theoretical calculations imply that they would just about explain away all the dark matter we observe, if their mass were in the 100 GeV range - the one favoured if they were the lightest SUSY particles.
This would really be a vindication of Ockhamism: SUSY - a theory which calls for the existence of hundreds of as-of-yet unseen new entities - would be proven correct because eventually it would kill many birds with one stone, its neutralino. But, no. After decades of investigation, SUSY particles remain at large, their appeal strongly dampened by the lack of evidence in the region of parameter space where they were for long argued to be most likely to reside.
Anyway, dark matter does not need SUSY to exist. There are literally hundreds of possible alternative explanations. Still, most of them still posit that DM is made of a neutral particle of very, very small interaction rate with ordinary matter. If that is the case, we know several things about this particle. First of all we know how many of them there are: more or less 300,000 per cubic meter, if their mass is equal to that of a proton (and 10^3 times more, if their mass is a thousandth). Also, we know they move "slowly": as the Earth moves around our galaxy, it seems likely that we are crossing a "wind" of these particles; this wind moves relative to us at about 100 kilometers per second, give or take a few tens.
Direct detection !
Physicists will not stand still with such an elephant in the room: let's go and discover this wind of DM! Enter the "direct DM experiments". These experiments try to find a signal of DM by looking at ordinary matter sitting in laboratories deep underground (where the background from cosmic radiation of known origin but enormously higher rate is reduced). If a DM particle hits a nucleon, maybe the reaction can be detected. It is extremely hard to detect such a small bump (100 km/s is a ridiculously small speed for subnuclear particles), but techniques do exist to hear the "sound" of these collisions, or detect other phenomena caused by the recoiling SM particle.
A host of experiments have been designed and operated to search for these rare collisions. A graph that illustrates this titanic effort is shown below. In it, the horizontal axis describes the unknown mass of the dark matter particle, and the vertical one sizes up, in logarithmic scale, the upper limit so far set by the different experiments on the rate of the DM-SM particle reactions (or if you want a slightly more technical term, the interaction cross section). The coloured lines show how the different experiments were able to set stringent limits on the interaction rate, and how these depend on the unknown mass of the DM particle.
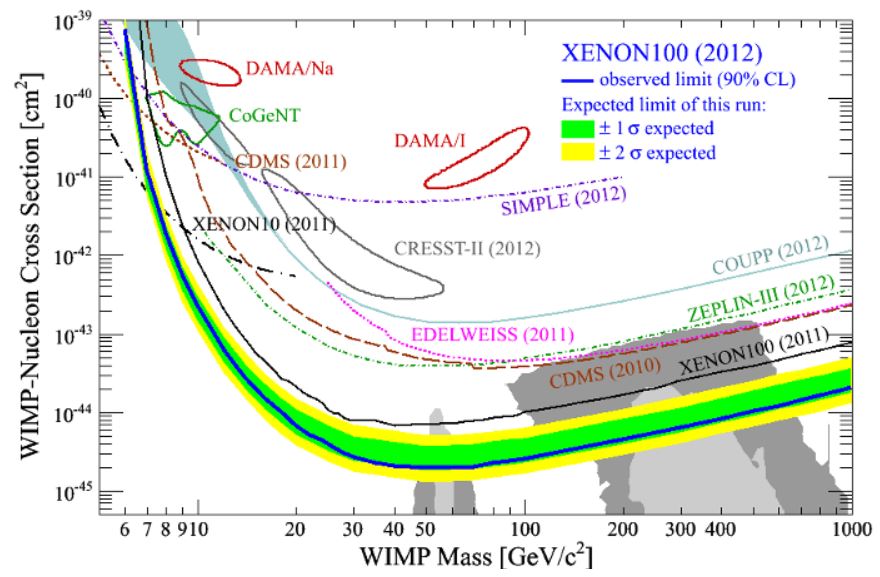
One feature that should not escape you in the graph is that none of the experimental search curves manage to put strong limits on the interaction rate for very light DM (the top left of the graph): if DM is very light, the bump they produce when they hit nucleons becomes so small that it is undetectable by any means.
I know what you may be thinking: "Surely, this mass region is the one where DM can reside - that's why it has been investigated so intensely". Well, yes and no. If you believe the particle you are looking for is a neutralino, then the interesting mass range is indeed in the 100 GeV ballpark; but if you are not constrained by that groupthink, you might well believe the DM particle is much lighter, e.g. This may then appear as a case of the drunkard searching for the lost car key at night: he only searches for it around the street lamp, as it is the only place lit up enough to see something, although he has a hunch he might have lost it elsewhere.
How could the drunkard illuminate the region of much lighter DM ? Well, there are ways. One way is to consider that while a light DM collision with ordinary nuclei will give them too little of a push to make a difference, we do have much lighter targets in matter: electrons. If a sub-GeV DM particle hits an electron at 100 km/s, it can still give it enough momentum to make it, e.g., escape a surface and become detectable.
A gedanken-experiment
I considered the possibility of detecting a 1-MeV DM particle as an exercise. Imagine you have a 1 square meter of insulator sheet, and you expose it to the DM wind. Occasionally, a DM particle will hit an electron located close to the surface of the sheet, and bump it off it. If there is an electric field capable of bringing the electron to some amplification device, you can get a signal. Collect the signal of the extracted electrons, measure a counting rate, and compare it to the corresponding counting rate you observe on the other side of the sheet: if the counting rate is higher in the direction where electrons should be extracted by the DM wind, you've won a ticket to Stockholm!
Alas, this is a theoretically working scheme but it is riddled with issues. The killing one is the background: you will never manage to construct a large-area detector with background counting rates low enough to make a signal visible, given how small a signal you expect. However, to convince yourself of this you have to make some calculation, which is a fun exercise. I will give you some starting data to play with if you like to try.
Let us consider that the cross section of DM with electrons be 1 femtobarn (which is 10^-36 cm^2), and that your target material contains 10^27 electrons (a 1 mm thick sheet of material should do). Now, assume DM has a mass of 1 MeV: this should allow you to derive the maximum kinetic energy of the hit electrons (hint: use momentum and energy conservation - this is a classical physics exercise and should be fairly easy).
Already you will see that the speed of the electrons makes their range in whatever material very, very short - your DM interactions would not allow the electrons to leave the sheet unless the latter were sitting almost on the interface (google "range of electrons" or something similar to get information on this bit); this reduces the 10^27 electrons of your target by three orders of magnitude (if the range is e.g. one micron). So, 10^24 electrons per square meter.
On the other hand you can compute the total number of collisions by considering that at 100 km/s, 300,000,000 DM particles per cubic meter (that's how many there are if their mass is 1 MeV) make a total of 3*10^13 of them going through our square-meter sheet. On the other hand, with a cross section of 10^-36 cm^2 each, the 10^24 electrons offer a total interaction area of 10^-12 cm^2, i.e. an interaction probability of 10^-16 per DM particle in a square meter of material. Hence you expect 3*10^13 * 10^-16 = 3*10^-3 interactions per second kicking electrons out of the surface. That's one event every five minutes of data collection.
Now, it does not matter that you certainly would have backgrounds from many sources - you only want to detect a difference of the rate on the two sides of the sheet. But still, you want to detect a very small rate! Let's imagine that we can exclude from consideration all signals appearing in coincidence on both sides of the sheet (crossing cosmic rays, e.g.). You would still have spurious dark noise in whatever detector you consider. How small should this be to make the DM interaction signal stick out ?
You want to measure D = C1 - C2, where C1 and C2 are the counts on each side. The uncertainty on C1 and C2 is Poisson, so these are sqrt(C1) and sqrt(C2), respectively. The uncertainty on D is consequently sigma(D)^2 = C1+C2, or sigma(D)=sqrt(C1+C2). If you are to measure an excess rate on side 1, e.g., this needs to be higher than a few times sigma(D) - let us say five times larger, so a "five sigma" excess on side 1. In one year of data taking, your collected signal would be of 100,000 DM interactions (one every 5 minutes, remember?). So this limits sqrt(C1+C2) to be smaller than 20000, a fifth of 100k, or sqrt(C1) less than 14000 (we assume C1 and C2 have equal expectation values, and only differ by random flukes). So you need a detector which produces less than 200M spurious counts in a year, or less than ten per second. That is hard in a square-meter counter.
Note that we started off with the hypothesis that the DM-electron cross section is 1 femtobarn - this need not be so: if it was a thousand times larger, would our scheme have any value ? Well, with a signal rate 1000 times higher, maybe yes! You could live with hundreds of spurious hits per second in that case, and still have a more than 5-sigma effect after one year of observation.
Of course, if one were serious about this, one would have to factor in the non-full-efficient signal collection, and other systematic sources. But on the plus side, nothing limits the experiment to have a single module! One could conceive, e.g., a stack of GEM detectors, maybe 100 of them... This would make the experiment 10 times more sensitive.
I hope this little fun calculation entertained you. For a more serious study of the interaction of dark matter with electrons, and the produced limits in cross section versus mass, I advise this recent article by the XENON collaboration.
----
Tommaso Dorigo is an experimental particle physicist who works for the INFN at the University of Padova, and collaborates with the CMS experiment at the CERN LHC. He coordinates the European network AMVA4NewPhysics as well as research in accelerator-based physics for INFN-Padova, and is an editor of the journal Reviews in Physics. In 2016 Dorigo published the book “Anomaly! Collider physics and the quest for new phenomena at Fermilab”. You can get a copy of the book on Amazon.





Comments