Two introductory words on SUSY
If you are unfamiliar with what Supersymmetry (SUSY) is, it may help you to know that it is a theory advocating a possible extension of the particle zoo. For each known elementary particle, SUSY predicts the existence of a corresponding "sparticle" with similar characteristics. Three things tell apart a sparticle from its normal counterpart: the spin, the mass, and of course the "s-" in their name (such as in stop, sbottom, selectron, setcetera), which puts them in a different category and earns them a different value of a quantum number called "R-parity". If R-parity is conserved, as in most versions of SUSY, sparticles can only decay yielding other sparticles, such that the lightest of them is perfectly stable, and constitutes a perfect candidate to explain the dark matter in the universe.
The idea of a supersymmetric world of sparticles, so far hidden from our view but ready to be found by the LHC, is not such an abstruse concoction to many: they will tell you that SUSY brings about enormous advantages from a theoretical standpoint.
One such advantage is the perfect "balancing" of particle and sparticle contributions to the quantum corrections on the Higgs boson mass, as I have explained in the second of my two recent articles in print on Physics World this month. In two words, the Higgs boson may be as light as we expect it to be (and as light as to make electroweak fits to observed standard model parameters look as good as they do) only if a score of quantum corrections to its mass produced by virtual particles coupling to it exactly cancel their total contribution. SUSY particles do that for free, since for every particle in the SM producing a contribution to the Higgs mass, a SUSY sparticle produces a variation of the opposite sign.
Another is the fact that with sparticles in the theory, there is a chance that we may one day explain all the forces of nature as the low-energy manifestations of a single interaction. This grand-unification is sort of a Graal for theorists, and they won't stop in front of having to add a hundred or so arbitrary parameters into their theory in order to pave the way to this prize. And Occam be darned.
The third one is the "dark-matter readyness" of SUSY: as mentioned above, SUSY provides a particle, the lightest neutralino, which might have been produced in large numbers in the Big Bang. These neutralinos would be just as heavy as needed to explain the observed amount of dark matter in the universe.
The ATLAS search
The analysis published in 1102.5290 does not present any real novelty with respect to previous searches, so I will not discuss the details here. Suffices to say that ATLAS goes for the production modes expected to yield the largest rate of superparticles: proton-proton collisions materializing pairs of squarks and gluinos. These are the super-partners of quarks and gluons, and they are produced in large numbers because they carry colour charge exactly as quarks and gluons do.
Some general features of the production and decay of these particles do not depend much on where exactly you sit in the complicated space of model parameters: gluinos and squarks are produced at higher rates if they are lighter; and gluinos decay to squarks or vice-versa depending on which particle is heavier. When these decays occur they produce an ordinary quark or gluon, which in turn may yield an observable jet of hadrons, if its energy is sufficient. The lighter supersymmetric particle may then produce other sparticles and other quarks, and the final decay chain usually includes a neutralino, which escapes leaving missing energy behind. The signature may be quite varied, but the general characteristics are always the same: jets and missing energy. It is always jets and missing energy, as sure as death and taxes.
ATLAS enforces the absence of electrons or muons in their candidate events. But electrons and muons are precious stones that very seldom get unearthed in the underground mine that a high-energy collision represents: why are they thrown away ? For two reasons.
One reason is that events with leptons have been considered already in a different search by the same experiment, and it is a good practice to keep different analyses looking for the same new physics signals "orthogonal" to each other, i.e. to allow no cross-contamination of the relative data samples: this makes it easier to compare the results and maybe combine them without having to worry about correlations.
The second reason for removing electrons and muons is that these particles are usually produced together with neutrinos in the decay of W bosons. Since neutrinos yield missing energy just as neutralinos do, removing electrons and muons is a way to reduce the annoying background from W boson production. Note that this "electroweak" background is not less troublesome to handle than the one arising from quantum chromodynamical (QCD) processes producing many jets, where missing energy is the result of jet energy mismeasurement (you fail to reconstruct properly the energy of a jet, and this automatically produces an apparent imbalance in the energy observed in the transverse plane, i.e. missing energy); the excellent properties of the ATLAS detector allow to keep the latter rather under control.
In the end, the main backgrounds are indeed still electroweak ones: W production yielding tau leptons and tau neutrinos, and Z production yielding neutrino pairs. Both W and Z bosons produced in LHC collisions are often accompanied by hadronic jets, and there you have your jets plus missing energy signature.
Some notes on the result
ATLAS optimizes the sensitivity to SUSY in different points of the parameter space by considering four slightly different signatures, involving two or three energetic hadronic jets whose kinematical characteristics best resemble those of the SUSY processes. In the end, they add up all the predicted background sources in each region, and compare with the observed data. Here is a summary of the results in the four search regions:
- Region A: total expected background 118+-35 events, observed 87 events.
- Region B: total expected background 10+-6 events, observed 11 events.
- Region C: total expected background 88+-30 events, observed 66 events.
- Region D: total expected background 2.5+-1.4 events, observed 2 events.
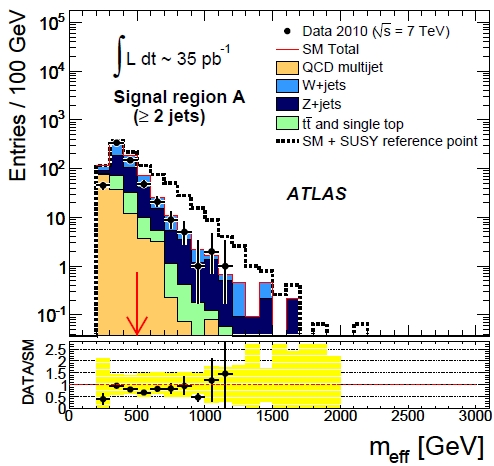 The "effective mass" (just a sum of transverse energies of jets and missing energy, so nothing more and nothing less than the standard "Ht" variable used in many past searches at the Tevatron) is shown in the figure on the right for region A. The signal region is for effective masses above 500 GeV (the red arrow). Data are points with error bars, backgrounds are stacked, and the SUSY contribution (for a reference point of the parameter space) is shown by the hatched histogram on top of the SM backgrounds.
The "effective mass" (just a sum of transverse energies of jets and missing energy, so nothing more and nothing less than the standard "Ht" variable used in many past searches at the Tevatron) is shown in the figure on the right for region A. The signal region is for effective masses above 500 GeV (the red arrow). Data are points with error bars, backgrounds are stacked, and the SUSY contribution (for a reference point of the parameter space) is shown by the hatched histogram on top of the SM backgrounds.Beware, in the list above I have been rough in combining the two main uncertainties in the background predictions produced by ATLAS; my point here is to show just that the order of magnitude of backgrounds agrees with observed data, and yet the latter is usually below expectations. This is good news for ATLAS, which can use this downward fluctuation to place more stringent constraints on the existence of additional processes (SUSY signal events) contributing to the data. The limits are shown as usual in the m_0 versus m_1/2 parameter space, having fixed to standard values some of the other model parameters. Their main result is shown below.

The point I made above on data fluctuating down acquires meaning if you remember that the same thing happened in the other SUSY search published by ATLAS two weeks ago: there, lepton signatures were considered for SUSY processes, and the search found a total of 2 events when four were expected. Again, a slight downward fluctuation of observed data with respect to backgrounds. Nothing dramatic in fact, but the small deficit allowed a significantly extended reach of the resulting exclusion in the space of SUSY parameters, with respect to what ATLAS predicted it would cover.
Am I just envious, since I belong to CMS, where we performed the same search described in the latest ATLAS paper but found more events in our dataset than expected,, so that we could produce a rather restricted exclusion region (the black curve) ?
No, I am not envious -I am actually convinced that SUSY is not there to be found, so I am prepared to see more and more of the parameter space being eaten up by experimental searches at LHC; the game will more or less go as follows: CMS excludes some region, ATLAS then excludes a bit more, then CMS takes revenge and extends the exclusion region with an improved analysis, then ATLAS does it, etcetera. This sort of game has been going on for quite a while at the Tevatron, and now that the players have changed the rules remain the same. Or do they ?
I only wish to note here that the downward flukes seen by ATLAS get compounded with a new method for limit-setting that ATLAS collaboration has decided to use for their new physics searches.
Now, this is a rather technical issue and I bet only two of the remaining five readers who reached this down in the article are really interested in knowing more about it. Okay, for you two I will make an effort.
Limit Setting: Black Magic ?
When you wish to set a limit on the rate of a new signal potentially sitting in your data by comparing background expectations with observed data, you are asking yourself the following question: just how much signal could, on average, contaminate my search region if I saw x events expecting y+-dy from backgrounds ?
Alas, the one above appears a quite legitimate and well-defined question, and yet the answer depends on the method you use to compute it. And there are quite a few methods on the market! It however appears that three of them are more "standard" than others, and as such they are discussed by the Review of Particle Properties. They are the Feldman-Cousins method, the CLs method, and the Bayesian integration with a flat prior probability distribution for the signal cross section.
Now, the method that ATLAS has started to use as of late is one which does not belong to the above list. It is a respectable method, although I do not personally like it much. Regardless of my own preferences, anyway, the chosen method might make comparisons of limits found by ATLAS with those of other experiments more difficult.
What is possible to say straight away is that in most cases the method used by ATLAS turns out to be slightly less conservative than any of the three "standard" methods. Together with the downward fluctuation, this puts ATLAS in the position of excluding more than competitors do of the SUSY parameter space.
One last issue I wish to mention this deep down my post is that the ATLAS 1-sigma band in the expected limits (see hatched blue lines in the figure above) is surprisingly wide in this last analysis. It looks strange because one expects that sparticle cross sections decrease quickly as one increases the m_0 or m_1/2 parameters in the plane shown in the figure. I would be happy if a reader provided insight in this matter. To me the width of that band is currently a mystery.





Comments