Ben Allanach is a professor of theoretical physics at the University of Cambridge. Before that he was a post-doc at LAPP (Annecy, France), CERN (Geneva, Switzerland), Cambridge (UK) and the Rutherford Appleton Laboratory (UK). I noticed a recent article of his in the arxiv, and asked him to report on it here, given the interest that the recent LHC results have stirred in the community. He graciously agreed.... So let us hear it from him! 

Blimey, I'm tired. I'm also elated and excited and grateful to my lovely girlfriend, who's not only putting up with my long hours, distracted head and general ensuing grumpiness, she's even looking after me. After twelve years of preparation, developing skills, mathematical algorithms and computer programs, papers are coming from the LHC experiments that are strongly constraining models of particle physics beyond the Standard Model. So, I've been pushing my limits, working feverishly hard on interpreting the data coming from the experiments while still performing the usual University duties, lecturing, examining and committees.

Twelve years ago I came to Cambridge as a post-doc at the Uni, and bumped into Prof. Bryan Webber having a glass of wine after a physics society talk in the physics department. We got chatting about scuba diving (Bryan's a keen diver and I'd wanted too give it a go) when he suddenly said "Oh yes, you've worked on supersymmetry before haven't you? Why don't you come along to a weekly meeting we're setting up with experimentalists here in the physics department?" At the time (and now), I was in the department of applied mathematics and theoretical physics (DAMTP). I'd worked on supersymmetric models beforehand, but not in terms of actually searching for supersymmetric particles at colliders. This was what the weekly meeting in physics was aimed at: the simulation and analysis strategies for finding new particles, with a particular eye on the LHC. The group became known as The Cambridge SUSY Working Group, and it's brilliant! The local theorists and experimentalists get together every week and discuss everyone's project of the moment: we give each other help and advice. People that are away at CERN still phone in to the conference, and our results are shown on private web-pages. I've learned so much from this group, and feel very lucky to be a part of it. This term I can't go to the meetings, because they clash with some lectures on supersymmetry (SUSY) I'm giving to master's students (curses). Anyway, attending this meeting and working with colleagues there has taught mean awful lot about interpreting data, experimental analyses and searches. There's no way I'd have been able to even contemplate interpreting recent data from the CMS detector at the LHC without the Cambridge SUSY Working Group.

The CMS results came out some 6 weeks ago: they were looking for any LHC proton collisions with high energy jets of particles accompanied by missing momentum. This can be interpreted as a search for supersymmetric particles (squarks and gluinos) because they decay into high energy jets of particles and neutralinos, which carry off momentum because they are invisible to the detector (they are the particle that many people think might constitute dark matter in the universe). CMS didn't find any significant excess of events with the right properties: so many squarks and gluons couldn't have been produced. The experimental paper produced exclusion limits in the plane of m_0 (related tothe squark mass) and m_1/2 (related to the gluino mass).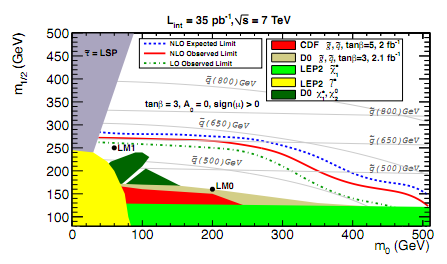

The models with masses below the red line are ruled out by the search, whereas heavier squarks and gluinos are allowed. That's because the LHC collisions haven't had enough energy to produce them yet (since E=mc^2, and so you need enough E to make more m). This is a simplification of course: actual collisions in the LHC are between constituents of the protons, and they carry some random fraction of the proton's energy in each collision. So, to some extent, you can probe further by just colliding more and more protons - thatis what's going to happen this year. But the big effect is when the energy of the collisions increases a lot: this is why the LHC results are going further than previous experiments (shown by the different coloured regions near the bottom of the plot).

Anyway, in the intervening 6 weeks, I've been working out what the results mean for simple supersymmetric models globally, once we take into account other constraints too. For example: if neutralinos really are the dark matter, then there are only some parts of the m0-m12 plane that give it density that's observed in the universe today. Also, there's a funny effect in the anomalous magnetic moment of the muon that (slightly) prefers quantum corrections coming from non Standard Model particles. This effect would like supersymmetric particles to be light. So we have a tug of war: under the hypothesis that supersymmetry is correct, some measurements would like the supersymmetric particles to be light, whereas the LHC is saying "they ain't that light". In this situation, you can do what's referred to as "a global fit". I wish that meant that everyone around the world suddenly dropped to the ground having a screaming temper tantrum. But a global fit really a way of carefully balancing the competing demands of the data on supersymmetric particles. We expect that the CMS results will push the supersymmetric particles to be heavier in the global fit, but the question is: how much? And are there any other less obvious effects? Knowing what the masses of the supersymmetric particles are likely to be allows us to make "Weather forecasts" for the next year of data taking: is it going to be raining supersymmetric particles, or will it be a supersymmetric desert? Actually, there is a very close analogy with what is done in weather forecasting, which is also done in an uncertain, somewhat random world. Also, we want to know how constraining the new searches are: are they reaching the supersymmetric masses that really fit the rest of the data (like dark matter etc) well?

What you see here in the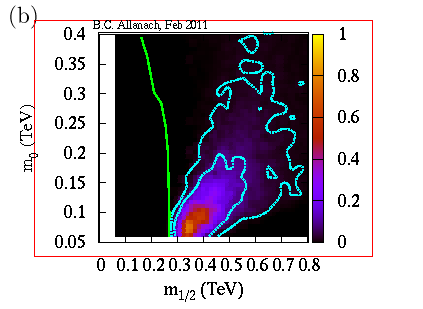

plot from my paper is the m0-m12 plane (sorry, it's flipped by a right angle compared to the one above), with the most likely place on it being the lighter colours, taking into account all of the data together. If the simple version of supersymmetry that I'm considering is right, there's a 95% chance that it lies within the outer turquoise curves. You can turn this into something more intuitive: a prediction of the squark mass probability, for example. That's shown here: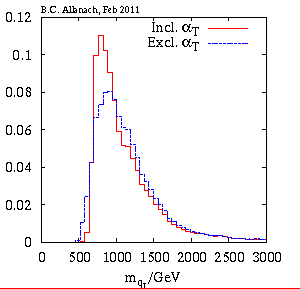

It's a "probability distribution": the higher the histogram, the higher the probability of the squark mass shown on the horizontal axis. This plot shows the difference made by the recent CMS search: before the search, I got the blue histogram, whereas including the search I get the red one. We see that small squark masses around 500-600 GeV become much less likely, but there is an interesting effect: squark masses in the range 800-100 GeV actually become more likely. That's because CMS saw a slight (not significant) excess in the number of collisions it was looking for, which prefers these intermediate masses. Anyway, the conclusion that with 95% probability, the masses remain below 2000 GeV bodes well: if weak-scale supersymmetry is the correct theory, it seems that the supersymmetric particles are likely to be light enough for the LHC to discover them, although they might take the energy upgrade to 14 TeV total energy in a couple of years).The frenetic work continues with new papers being released every week, all based on last year's data. I worked on the CMS results alone, because my Cambridge Supersymmetry Working Group friends were too busy working on important experimental analyses to help. You may ask how I've now got time to write this blog? Well, luckily, some of my SUSY working group colleagues (Teng Khoo, Chris Lester and Sarah Williams) have now got some time to play with me on the next paper on ATLAS results, which is a huge relief. My girlfriend is still being lovely to me, despite the strains I'm placing on myself/us. Imagine how feverish we will get if/when there's actually a strong new physics signal: I imagine there'll be a lot of Star Wars in physicists' marriages (May Divorce Be With You).