Mysterious Symmetry between Destruction and Growth asked “How on earth does blowing stuff up violently constrain unrelated growth mechanisms? This is the mystery.”

In the science of ultra cold Helium droplets of nanometer sizes, there exists a simple, widely known formula, which basically states that the sizes of such droplets obey an unexpected symmetry. This is possibly significant for many similar statistical processes, say during earthquakes or on the stock market. It would be astonishing if Helium droplet physics could investigate this general phenomenon that may hold in quite different destructive and constructive random processes in biology, nanotechnology, and many other important fields.

The symmetry in the droplet sizes seems to be the following: Their average size equals the fluctuation of their sizes. If you count the number of atoms N in a droplet, the surprising relation can be written as Average(N) = Δ_N, where “delta N” measures how widely the sizes differ.

This is unexpected; there is no physical reason that could constrain the system in such a way. It seems to hold for growth processes, where it is completely unexpected, but also for violently destructive processes, where it seems better understood, and here is the thing: Helium cluster physics can kind of smoothly go from one regime into the other. Maybe this unexpected symmetry in random growth processes can be described as ‘inherited’ from the destructive regime and thus the underlying science of growth can be better understood. [6]

This is also interesting for applied physics, especially nanotechnology, where the relation between average and fluctuations around the average often renders fluctuations too large: If you need sizes near a certain, large average, you do not want most of the samples being much smaller and much larger than specified.

It is entertaining to think up a hypothesis about why the strange relation holds. This was attempted in the comment section of Mysterious Symmetry between Destruction and Growth. The actual solution to the mystery is a big let-down however, yet it is nevertheless an important, not widely enough appreciated lesson.

The symmetry is an artifact! [7] It is not empirical, but instead stuck into the experiments via assumptions about how the measurement behaves, and then again into the analysis of the already biased data. Let us here focus on the second aspect.

What has been done is to assume simple functions that have only few degrees of freedom and that are mathematically convenient. That is of course fine and simplification is what makes physics powerful. This is good science as long as you stay aware of what your simplifications are and how they propagate through your scientific methods.

Sadly, awareness is largely missing, and so the assumptions often pop up in transmuted form in the results, giving rise to “discoveries”. In this case, several factors helped to construct a symmetry where there is none. Another case for the sociology of science supporting its charge that much of scientific fact, empirical as well as theoretical, is constructed.

The mistakes that were made are simple. One is to transform forth and back between parameters, here N for example, and their logarithms like n = log(N), during the analysis, putting assumptions in at different stages. Since for large numbers, the differences in their logarithms are still rather small, a careless treatment easily loses information, thus 'justifying' simple assumptions.

But the biggest of the many mistakes made is the general use of what is called parametric statistics. Parametric statistics assumes a certain kind of distribution from the outset, for example a so called log-normal distribution LN (see red one below). The assumed distribution has parameters, here the average Average(N) and the deviation Δ_N. Then, the data are fitted with that distribution and only the parameters Average(N) and Δ_N are extracted. Or in case of the exponential distribution EXP (green one), only one parameter, namely Average(N) is extracted.

 While decays and fractionations lead often to power laws and exponential (EXP) distributions[1,2], random grow processes give mostly rise to so called log-normal (LN) distributions, be it in biology, economics, or cluster physics [3,4,5].

Parametric statistics is good and proper as long as you keep aware of what you are doing. However, it happens fast that your assumptions start a life of their own, namely that you (or a whole scientific field in this case) start to assume the assumed distributions are not just what worked reasonably well for pioneering purposes, but that by now it has become established that they actually are the distributions that are physically present. Forgotten the fact that when the whole thing started, the data could have been equally well fitted with other distributions that would have led to different extracted parameters.

In this case, the core of the mystery of the hidden symmetry is double ridiculous, as it is differently ridiculous for the LN and the EXP. Lets deal with the LN:

What was done is to extract the logarithmic parameters, that is not Average(N) and Δ_N, but instead Average(n) and Δ_n, where n = Log(N). These parameters were then transformed into variables in N-space, namely Average(N) and Δ_N, that both depend strongly on Average(n) but only weakly on Δ_n. Note, for statistical distributions, Δ_N for example depends more on Average(n) than on Δ_n; this may be counter intuitive but it is rigorously true.

So, it was now ‘established’ that Average(N) is somehow bound to Δ_N as if one degree of freedom just vanished. It vanished because the employed method artificially suppresses the influence of one of the measured parameters. This was helped along by the use of a particularly bad dispersion parameter, which is the full width at half maximum (FWHM) in this case, but let’s not get too technical.

Apparent fixing by unsuitable use of measures: Two measures of the deviation of cluster sizes N are plotted versus the average <n> of n = ln(N): The square of an often presented measure, namely the average <N> divided by the FWHM, remains fairly constant (white dots) while the dispersion relation d_N decreases strongly with <n> (black dots).

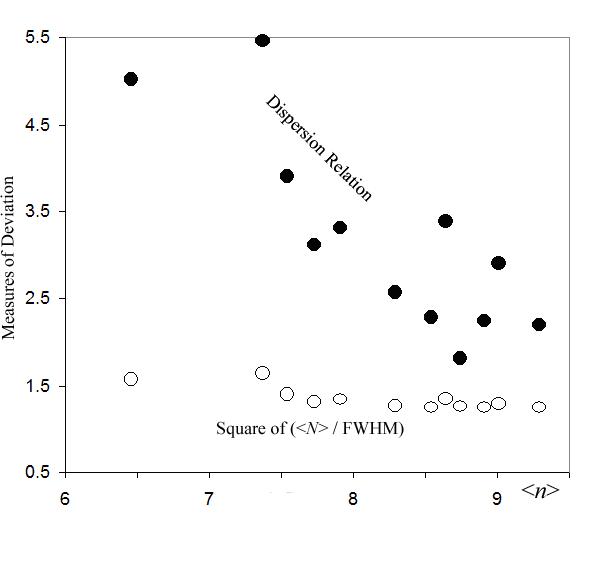
Remember, the most intriguing is that the same relation seems to hold also in the destructive regime where the EXP distribution is assumed. Here it turns out that the distribution was actually only ever fitted for large N. The EXP looks similar to many other distributions for large N, for example the gamma distributions.

The relation Average(N) = Δ_N holds in a sense accidentally for the EXP. This fixation can be expressed in log-space as Δ_n= Pi/(Square root of 6). Now recall that in the LN growth regime, Δ_n is a data derived fitting parameter that varies with Average(n). Surely it is ‘funny’ if one research group defends Δ_n as an adjustable parameter that is the best one to follow experimentally while another group’s assumption amounts to Δ_n being a fixed, weird mathematical constant. One or the other is obviously false.

The conclusion is one that has consequences in many fields far beyond nanotechnology and cluster physics. The careless use of parametric statistics is widespread, for example in medical research. Again, parametric statistics is fine as long as you are careful about how your assumptions shape the results.

One practical advice is to employ different assumed distributions, like the gamma distributions that should fit the data much better. These are not always more difficult mathematically either. For this reason, several promising distributions were suggested [7][8] that can be used instead of the LN and the EXP. The alternatives are even more convenient for certain important tasks. [8]

But it is an uphill struggle. The assumptions of EXP and LN have now almost become dogma for example in the Helium cluster sub-field. Hence, the simplified assumptions are re-entrant into the data-analysis, persistently, and all data implicitly depend already on these assumptions. One cannot find real raw data in any of the varied experiments, because the assumption of the simple size distributions and simplifying Poisson collision statistics are already implicitly stuck inside. It is practically impossible to get away from it, and so knowledge is being constructed.

Not surprisingly, any criticism is silenced by peer review. A new case study for the sociology of science has emerged, but as a referee in that, at least equally dubious field once pointed out to me, the sociology of science is not in need of people suggesting new case studies of constructed knowledge; they have far too many already. This is certainly true.

------------------------------------

[1] D. E. Grady and M. E. Kipp, Journal Appl. Phys. 58, 1210 (1985)

[2] B. L. Holian and D. E. Grady, Phys.Rev. Lett. 60, 1355 (1988)

[3] M. Villarica, M. J. Casey, J.Goodisman, J. Chaiken, Journal of Chemical Physics 98, 4610 (1993)

[4] C. R. Wang, R. B. Huang, Z. Y. Liu, L. S. Zheng, Chem. Phys. Lett. 227, 103 (1994)

[5] E. Limpert, W. A. Stahel, M. Abbt, Bio Science 51, 341 (2001)

[6] S. Vongehr: Helium Clusters’ Capture of Heliophobes, Strong Depletion and Spin dependent Pick-up Statistics, USC Dissertation, ProQuest AAT 3219885 (Los Angeles, 2005)

[7] S. Vongehr, S.C. Tang, X.K. Meng: On the Apparently Fixed Dispersion of Size Distributions. Journal of Computational and Theoretical Nanoscience, 8(4), 598-602 (2011)

[8] S. Vongehr, S.C. Tang, X. K. Meng: Collision statistics of clusters: From Poisson model to Poisson mixtures Chin. Phys. B 19(2), 023602-1 (2010)