A new technique for studying turbulence in quantum fluids used a mechanical resonator, a miniscule bar 1/1000th the width of a human hair, in superfluid helium near absolute zero temperature to effectively 'trap' a single vortex for study.
Sound complex? That's easier than modeling the turbulence in a river or anything else, which is basically impossible. Better models of something simpler like quantum turbulence - yes, you read that correctly - might help.
Looks simple, right? A tree branch is also linear until you apply just enough weight it goes nonlinear and breaks. Yet no one can say with certainty what precise weight it will take.
The Navier-Stokes equations are partial differential equations and in simple form it means a true answer can never be derived but a simpler answer can only be 'converged' on. Any young engineer told to 'assume non-laminar flow in an infinite aerofoil' has likely had a 'wait, we are putting people in machines trusting that?' moment.
In the quantum realm, turbulence in fluids is simpler because they consist of identical singly-quantized vortices, so they can perhaps be a model for turbulence in the world we experience.
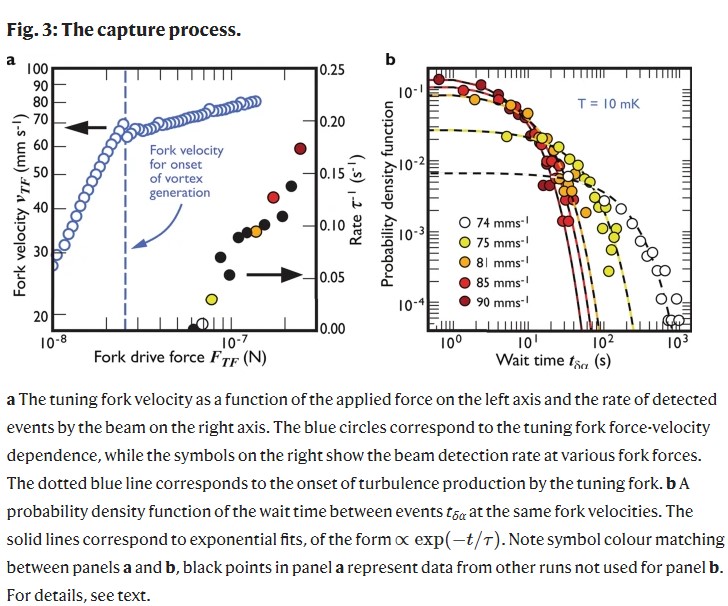
For their study, the authors rightly like it to a real world resonator, a guitar string, but you can use a tuning fork or anything else that changes frequency due to energy. When a vortex gets detected the resonant frequency of the bar/string changes. By catching and releasing vortices they can measure the changes. The capture was recorded with an oscilloscope and the tuning fork was also measure old school, with a vector network analyzer.
You'll probably not that with no meaningful friction this is limited, and that is true, but if the goal is understanding quantum turbulence, and then visible turbulence, it's good proof of concept.
'Solving' the Navier-Stokes equations, which means solving turbulence, is one of the most challenging problems in math but turbulence is not alone in being poorly understand physics that we nonetheless leverage to our benefit. The device you are reading this on works thanks to Maxwell's equations, which can also never be solved. It is impossible to even define a magnetic field without being recursive (a field in the presence of a magnet) and yet electric and magnetic fields are fundamental to a trillion dollar industry.




Comments