My trip to the University, in Padova, begins with a 7-minute walk to the Venice train station, followed by a 40 minute ride and then a further 15-minute walk in Padova to reach the Physics Department. While on the train I usually busy myself with document editing on my laptop, but on my walks I use to try and put to work the other main CPU I have got - my brain.
Upon enjoying the glory of Venus, this morning I was caressed by the idea of computing by heart the number of photons that reached my pupils from the planet every second. I love to compute things by operating approximate estimates of the physical quantities, and -in the lack of precise information, by sheer guesswork (that's where the real fun is). It is indeed a lot of fun, if you get to develop a little practice. Today I wish to show you how easy it is to compute things by heart, using the "photons from Venus" question as a worked-out example.
I know the number already!
To begin with, I must say I knew the answer rather precisely before I even started out my calculation. That's because my brain's database contains a lot of apparently useless bits of information! I just needed to combine two of them, as follows.
Venus has an apparent magnitude of about -4.5, and is thus eleven magnitudes brighter than the faintest stars we can appreciate with the unaided eye in a clear, moonless night (these have visual magnitude of +6.5, roughly). Eleven magnitudes equate to a 25,000 factor in brightness. That is because of the astronomical definition of magnitude: the ratio of the light intensity of two luminous objects is 2.512 if these objects have magnitudes that differ by one unit; the factor 2.512 is the tenth square of 10,000, so 2.512 to the 11th power is 25,000. As easy as pie.
It remains to know (as I happen to) that the faintest stars we see send into our retina about 2000 photons of visible light per second, (this is by no means a trivial datum, and it is the result of experimental investigations[1]) and we are done: Venus must then yield about 50 million photons per second, as a fourth grader could compute by just multiplying 2000 by 25,000!
A more exhaustive derivation
Okay, that was the short route, and the least interesting one. Let us instead take the long one, to set up the calculation I did by heart this morning as a challenge to myself. We will compute the power received by Venus due to its facing the Sun, and then, factoring in albedo and geometrical factors, deduce the fraction of that power which is intercepted by our retina on Earth. We can finally convert that power into a rate of photons with some more wrestling of physical constants. Simple ? Hard ? Let us see.
I do not know off-hand what power arrives on the surface of Venus by the Sun, but I can figure that out easily, since I do know how much radiating power arrives on Earth: this is a well-known quantity, called "solar constant", and is equal, if I am not wrong, to 1.4 kW per square meter. Since Venus is 1.5 times closer to the Sun than we are, the power it receives per unit area is 1.5 squared, or 2.25 times larger. This is easy to understand, since the sphere centered on the Sun on which Venus lays has a surface which is 4*pi*R^2, where R is the Venus-Sun distance; make R larger by a factor of 1.5, and the surface increases by 2.25, so the unit-area flux decreases by the same factor.
Fine, so we know that the Venus atmosphere receives 1.5x2.25=3.15 kW per square meter from the Sun. But how much is the total power ? That requires us to know the surface of Venus as seen from the Sun: a disk with the diameter of Venus intercepts the flux within an area of pi*R^2, with R the radius of Venus. This is about 5000 km (off the top of my head), so 5 million meters. The intercepting surface, in square meters, is thus 3.14 times 25 times a trillion, which we better store in our brain's memory as "eight times ten to the 13, give or take a cow's crap". In scientific notation, this is 8 * 10^13 m^2.
Two possible solutions...
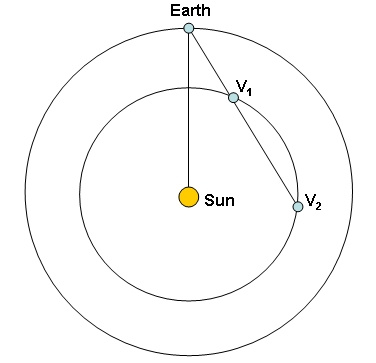By multiplying power flux by surface we obtain that the power received by Venus is in the whereabouts of 3.15 kW times 8 times 10 to the 13, which is easy to convert to 25 times 10^16 Watts (a kiloWatt, kW, is a thousand Watts). How much of that flux is sent in our direction ? Well, that depends on the phase of Venus -of if you will, the angle it makes with us and the Sun. Here, experimental observation came in handy: I saw Venus at about 35 degrees elongation just before the Sun rose, so I take that value as good for my calculation. At such an angle, there are two possible positions where Venus may be with respect to the Earth, and two corresponding Earth-Venus distances, as shown in the sketch above. If I were a more constant amateur astronomer, I would certainly know where Venus is, but I don't... Ouch. We need to compute two different flux factors for the two cases.Fear not, it is not that hard, although here you need to know at least roughly what is the geometry of the two planets' orbits around the Sun. It is sketched on the right: as already reported, the radii of the orbits are of 100 and 150 million kilometers, so we gather that, roughly speaking, if Venus happens to be in the position labeled "V1" it is at a distance of 70 million kilometers, i.e. about half the Earth-Sun distance; in the other case the distance is larger. During my walk I guesstimated a value of 100 million kilometers, but I am much worse at geometrical calculations by heart than I am with math operations! Here, let us take 190 million kilometers as a better estimate.
As for the flux that is sent in our direction, that requires us to know the apparent fraction of Venus surface lit by the Sun from our direction. Again, here we must make rough estimates. In position V2 Venus will almost show a full disk to us -let's say 80% of it will appear lit by the sun (something like the image labeled "Aug." on the right); in position V1, however, the situation will be much closer to the one shown on the left, for which we can estimate a lit fraction of 30%, give or take a few (something between the aspect of "Jan." and "Feb.").One more step - the fraction of flux intercepted by our pupil!
From position V1 Venus is at 70 million kilometers, i.e. 7 *10^10 meters from us. We lay on a sphere centered on Venus with that radius, and the sphere has a surface of 4 times pi times radius squared. Now, four times pi is 12.5, seven squared is 49, and the square of ten to the tenth is ten to the twentieth. All together this is 12.5 times 49 times 10^20, or 6.2 times 10^22 square meters.
From position V2 we are instead 190 million kilometers apart, or 1.9 times 10^11 meters, so the calculation yields a surface of 4 times pi times the square of 1.9 * 10^22: the result is 12.5 times 3.6 times 10^22, or roughly speaking 4.5 times 10^23 square meters.
One good thing is that despite the two different configurations of the problem, the dimensions of our eye pupil do not change: it is roughly a circle of radius 3 millimeters, so its surface is 3.14 times 0.003^2 square meters, or 28 * 10^-6 square meters. This is quite a small fraction of the total solid angle from Venus! From V1 the ratio is 28 * 10^-6 divided by 6.2 * 10^22, or roughly 4.5 * 10^-28. From V2, the ratio is even smaller: 28 * 10^-6 divided by 4.5 * 10^23 equates to 6.2 * 10^-29.
By multiplying in turn those two fractions by the Venus power flux sent to us, we get the power sent by Venus into our eye pupil from its two possible locations. But before we do that we must consider that not all of the luminous radiation hitting Venus is sent back! A fraction is absorbed. The reflected fraction is called "albedo" and it is a number between 0 and 1. We may take 0.5 for Venus -I have a feeling it is larger, due to the many whitish clouds that constantly hide the planet's surface from our view, but cannot fool myself into feeling secure of that: so let us approximate here.
So we had an emitted power of 25 * 10^16 Watts, which we multiply by 0.5 for the albedo. This makes 12.5 *10^16 W. Then we multiply by the observed lit fraction of Venus from the Earth, and further multiply this by the fraction of flux which our eye pupil intercepts in the two cases.
From V1 we get 12.5 * 10^16 times 0.3 (Venus phase) times 4.5 * 10^-28 (fraction of intercepted flux). 12.5 times 0.3 is 3.75, 3.75 times 4.5 is 17, and the total is thus 17 * 10^-12 Watts.
From V2 we have 12.5 * 10^16 times 0.8 (Venus phase) times 6.2 *10^-29. This is roughly 62 * 10^-13 Watts.
The final step
Now we have the power flux from Venus into our eye pupil! We could be quite happy already of our calculation, but we have a final step to make. We need to convert the power from Watts to number of visible photons per second, and to do that we know how much energy does one visible photon possess. Here I must declare my ignorance -I think visible photons carry and energy of the order of a couple electron-Volt, but I am not too sure! I will take 2 electron-Volts for the energy of a visible light quantum, knowing I might be wrong by a factor of two or three here.
(The photon energy could be derived by looking up Planck's constant value in eV*s, and multiply it by the frequency of visible light, which in turn is the speed of light divided by the wavelenght; I know the wavelength -about 500-600 nanometers- but I do not recall the value of Planck's constant in Ev*s! So I just guessed a value.)
One Watt is 1.6 times 10^19 electron-Volts (this number is the number of electrons making up a charge of one Coulomb -it is a good number to remember!), so it takes 8 billion billion 2-eV photons (8 * 10^18) per second to make a Watt. But we have only 17*10^-12 Watts in the first case, and these then equate to 17*10^-12 * 8 * 10^18 = 150 million photons per second; in the second case, 62*10^-13 * 8*10^18 = 50 millions per second.
Final notes
Remarkably, we have recovered the order of magnitude I quoted at the start ! Please note a few things here. First of all, as I walked to the train station I was much more willing to produce rough approximations than here, as I more thoughtfully write down things. By heart I omitted to include an evaluation of the fraction of surface visible from Earth, and I approximated the Earth-Venus distance with 100 million kilometers. Despite these shortcuts, I came up with a very similar answer to the one I quote above.
The other thing to note is that while writing this piece I have deliberately omitted checking any of the constants entering the calculation. I did not verify what is the energy of a quantum of visible light; I did not check what is the albedo of Venus; I did not bother to verify which is the correct phase of Venus today. What's worse, I have some doubts on the validity of the Sun's flux on Earth's surface! I am thus prone to pitfalls if I post this article as is. On the other hand, the whole point and the whole fun of computing things by heart is to try and exploit only the information we remember, without looking them up!
I believe that it is quite educative to perform calculations by heart. Of course you might want to start with simpler things. One nice calculation I suggest is to calculate how many calories you burn in a year, if you walk up the stairs to your office in the morning every working day instead than taking the elevator, or if you walk there from home instead than taking the bus; you can translate that into pounds of fat you would burn if you wish. Except from trivial formulas for potential energy and the gravitational acceleration on Earth's surface, all you need here is the mechanical equivalent of a calorie -ok, you may look that one up!
So try it! And then let me know what answer you come up with. Make it personal and detailed, and we will all enjoy your considerations.
---
[1] D.A. Baylor, T.D. Lamb, K.W. Yau, "Response of retinal rods to single photons." Journal of Physiology, Lond. 288, 613-634 (1979)
Comments