That volume intersecates the plane which corresponds to the Standard Model prediction: the Standard Model does not predict the mass of the three heaviest particles any more than it predicts the mass of the lightest ones, but its inner workings (so-called "radiative corrections" due to quantum loop processes involving the top, the W, and the Higgs) connect the three parameters in such a way that given two of them, the third one is fixed. A one-dimensional constraint in three dimension equates to reducing the dimensionality to two: hence, a plane in 3D.
And the MSSM ? The minimal supersymmetric extension of the Standard Model is not a single theory; rather, it is a collection of theories, depending on the value of a number of additional parameters.
It is therefore not surprising that the MSSM does not yield a decrease in dimensionality of the allowed regions of the three-dimensional phase space; it rather selects a preferred volume, which depends on some of its parameters. In particular, we know that for a choice of heavy sparticle masses, there is still compatibility with the measured top, W, and Higgs boson masses. Of course the "Higgs" here is just a neutral scalar, one of the five Higgs bosons that the MSSM predicts. For some choices of MSSM parameters, that light neutral Higgs behaves quite similarly to the Standard Model one, such that present measurements would not have seen anything deviating from SM predictions yet.
The figure below, courtesy Sven Heinemeyer, shows the "MSSM view" of the mW - mtop plane. The third dimension, the Higgs mass coordinate, has here been shrunk and we plot what happens for just the measured Higgs mass, 125.6 GeV; but it is useful, I think, to consider that parameter as well. As you take the Higgs mass to increase from 125.6 GeV to higher values, the SM prediction, the diagonal line in the graph, moves down toward the bottom right corner. The MSSM green area also moves around; note that a wider range of Higgs masses is allowed for the MSSM in the graph.
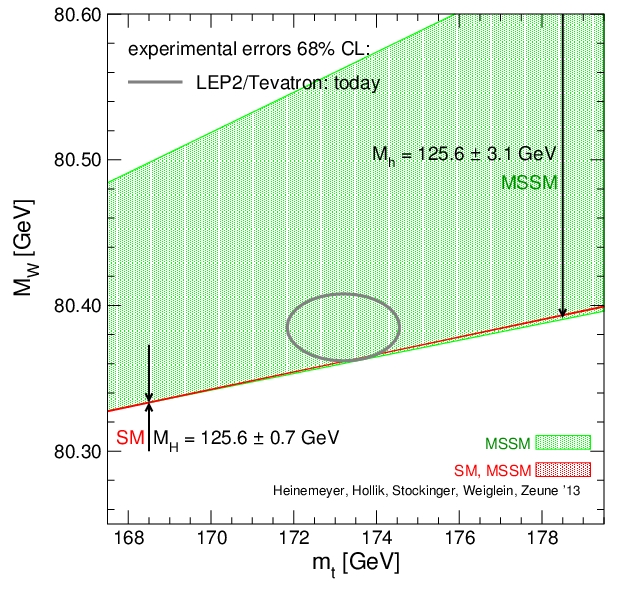
By looking at the graph, we learn that the MSSM is compatible with a much broader range of masses of the three considered particles. For sceptics, the insistence of precision measurements to include parts of the SM "plane" (the diagonal line) while reducing the allowed area of MSSM theories that remain compatible with the data (the area encompassed by the black oval, including 68% of the probability density compatible with the experimental measurements) is a proof that the MSSM is getting more and more unlikely; for enthusiasts, however, the fact that some SUSY parameters still agree with the observations is a reason to keep a strong faith. Your pick!





Comments