The concept of probability is not alien to even the least mathematically versed among us: even those who do not remember the basic math they had in primary schools use it currently in their daily reasoning. I find the liberal use of the word "probability" (and derivates) in common language interesting, for two reasons. One, because the word has in fact a very definite mathematical connotation. And two, because the word is often used to discuss the knowledge of a system's evolution in time without a clear notion of which, among either of two strikingly different sources, is the cause of our partial or total ignorance.
1. As far as the mathematical flavour of the word is concerned, it is sufficient to note that its loose usage directly involves the eyeballing of a real number taking on values between 0 and 1. Whether you are talking about the chance that a colleague missed the train given that she is not showing up, or whether you am wondering who might win at Roland Garros next June, the moment you say "Susan is usually on time, so it is highly probable that she missed the train" or "Nadal has a high probability of winning next year, especially if Federer does not play" you are guessing that a real number is significantly larger than zero. You might even inconsciously be assigning it a definite value, if you are taking a decision: start the meeting anyways, or accept your friend's bet against Nadal.
2. Few of us, in using the word "probability", spend a moment of their time pondering on the real meaning of the word, and the fact that what it usually does for us is to explicitate our imperfect knowledge of the state of a system, or, in many cases, its past or future evolution in time. Our ignorance may be due to two quite different sources, although we usually fail to realize the difference: the intrinsic randomness of the phenomenon we are considering (say, if we try to predict the future, like the participation list of next years' Roland Garros), or the insufficient data at our disposal on a system which is perfectly deterministic, id est one that has already taken a definite state, however unknown to us (Susan took the train or missed it).
Note that for statisticians the above statements on Susan or Nadal are guesses, not estimates: estimates come exclusively from measurements! Yet similar sentences get as close as anything to scientific thinking for non-scientists in their everyday life. The reason why they do is that they implicitly use Bayesian reasoning. If you do not know what Bayesian reasoning is, read on: you might realize you are smarter than you thought.
Two schools of thought
There are two schools of thought when discussing the probability of different hypotheses. One school is called "Frequentist". If I were using frequentist thinking, I would say that observing the behavior of an infinite number of readers N of this post would allow me to compute the probability that you leave it before getting to the end, by taking the limit, for large N, of the fraction of departures divided by N.
The other one is called "Bayesian" after Thomas Bayes, who formulated in the mid 1700s the famous theorem named after him. Bayes' theorem was published postumously in 1763 by a friend, who beat on time the mathematician Pierre Simon Laplace. For a Bayesian, probability is not a number defined as a fraction of outcomes, but rather a quantity defined irrespective of the possibility of actually counting a fraction of successes: one which has to do with the degree of belief of the experimenter. This belief sizes up the likelihood one may assign to the occurrence of a phenomenon, based on his or her prior knowledge of the system.
Being a Bayesian -at least in everyday life-, instead of fantasizing about infinite readers I use my prior experience on similar articles I wrote, and the data provided in this blog's access statistics, to try and put together my guess: in statistical jargon, I assign a "subjective prior probability" to the dropping out of readers during a long piece, depending on its length and subject. Since the number in this case comes out pretty close to unity -a certain outcome-, let me get to the heart of this post quickly. I want to convince you that you, too, are a Bayesian. But I need to explain you the theorem first!
Bayes' Theorem
If you are here in search of a rigorous definition, you have come to the wrong place. I will give in the following a simplified, inaccurate explanation of this important tool in statistics, by considering an example. As I just had occasion to note, I am a Statistician only by election...
It all revolves around the meaning of conditional probability. We may call C a restricting condition on the occurrence of a phenomenon A, and write the probability of occurrence of the condition C as P(C). Similarly, the probability of the phenomenon A may be labeled P(A), and the probability of occurrence of A under the restricting condition that C also occurs as P(A|C).
In our Nadal/Federer example above, we might assign to C the meaning "Federer plays Roland Garros 2010"; A will mean "Nadal wins RG2010", and A|C is what we want to know, namely "Nadal wins RG2010 if Federer plays". Bayes' theorem then can be stated as follows:
The probability P(A|C) that "Nadal wins RG2010 if Federer plays" can be computed as the product of three terms: P(A), the probability that Nadal wins; P(C|A), the likelihood that Federer plays if Nadal wins; and 1/P(C), the inverse of the probability that Federer plays. In symbols,
P(A|C) = P(A) P(C|A) / P(C).
Let us give P(A) a 30% chance: the overall chance that Nadal wins. This is our subjective prior, our degree of belief on Nadal winning. Then if P(C), the chance that Federer participates, is 90%, and the likelihood of Federer being there if Nadal wins is 60%, we get for P(A|C) the number of 0.3*0.6/0.9=0.2, or 20%. In this example, a good part of the chance of Nadal winning Roland Garros comes from Federer not coming. Note that somebody else might assign a different probability to P(A), and his result for P(A|C) will in general be different. This is at the heart of what makes Bayes theorem controversial among Statisticians.
I think what is counter-intuitive in Bayes Theorem is the fact that to compute a conditional probability P(A|C) we need to consider the case where we switch the place of the conditioning clause and the main phenomenon which is the object of our attention, by evaluating P(C|A). But there is really nothing mysterious, if you consider a graphical interpretation of the theorem.
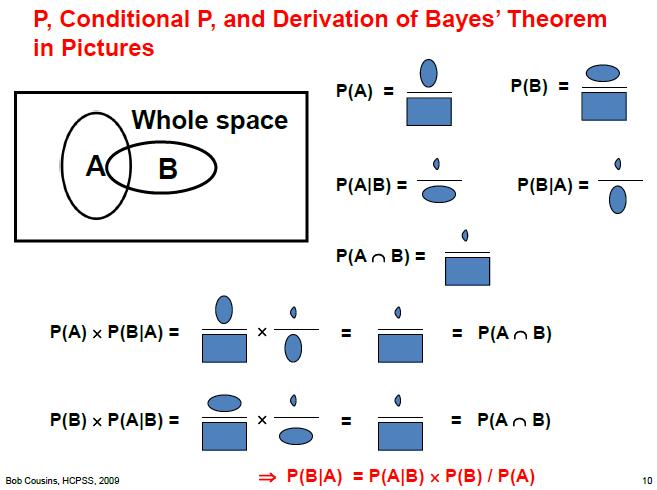
To interpret the figure above, which I have stolen from the enlightening slides of a course held last summer by a colleague, you are asked to liken probabilities to areas on a plane. Our "universe of possibilities" is the big rectangular box; then, the occurrence of phenomena in this universe can be represented by smaller areas within the box. The other thing you need in order to decrypt the slide is the meaning of symbols of union of sets and intersection of sets: A "U" symbol between two clauses labels "union", and indicates the logical or of two clauses, while the symbol looking like a upside-down "U" labels "intersection", and indicates the logical and of the two clauses.
I find the graphical demonstration above quite simple to grasp, and I hope you will concur. I have always wanted to put together a similar slide but I was happy to be saved the work... Thanks Bob!
Conclusions
I think you will be wondering why on earth you should consider yourself a Bayesian, since the theorem above looks obscure to you and you never even dreamt of computing conditional probabilities or subjective priors. Well, I think you do, inconsciously. When you have to take a decision in your daily life you are most likely to rely on your past experience on similar situations, but in the toughest cases that experience will not be available, and what you will draw from it will be a "degree of belief", which you build by extrapolation or other kinds of logical reasoning. If you ask yourself what is the chance that Susan took the car to drive to work today, if she is not there by the time the meeting starts, you will need to consider the probability that Susan is late at work when she takes the car, and this may be known to you from past experience; but you also need the overall probability of Susan taking the car, and this might be only available to you as a personal degree of belief. You will most probably not end up multiplying P(took car) by P(late|took car) to get your feeling on the chance that she is arriving by car, but your intuition will be based on those concepts anyway.
Then, there is another reason why you are probably using Bayesian reasoning in your everyday life, and that is its application to risk analysis. But I think I need to stop this article here: my risk analysis of dropping readers makes the price of writing another page not worth the while... It will be a wonderful topic for another post, if I manage to put together a few particle physics examples. Not your everyday bread and butter, I know, but at least more interesting than discussing chances of winning at the Casino. Or so I think.





Comments