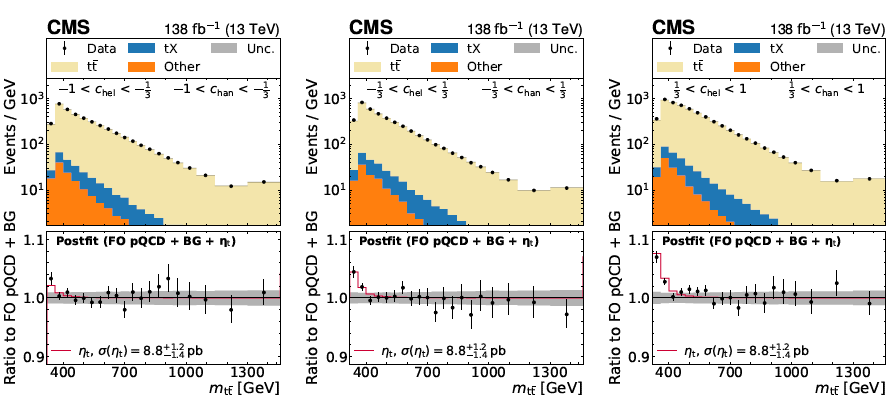
The highest-mass subnuclear particle ever observed used to the the top quark. Measured for the first time by the CDF experiment in 1994, and subsequently confirmed by CDF and D0 in 1995, the top quark is the heaviest elementary particle we know of, and it is a wonderful physical system per se, which has been studied with momentum in the past thirty years at the Tevatron and at the LHC colliders.
The top quark
In a world where misinformation, voluntary or accidental, reigns supreme; in a world where lies become truth if they are broadcast for long enough; in a world where we have unlimited access to superintelligent machines, but we prefer to remain ignorant; in this world we are unfortunately living today, that is, the approach taken by scientists to accumulate knowledge - peer review - is something we should hold dear and preserve with care. And yet...
In the past few years my activities on this site - but I would say more in general, as the same pattern happened also on social media - have progressively shifted away from pure casual blogging and reporting of personal matters to a more focused discussion of scientific topics, always lingering around my research interests.
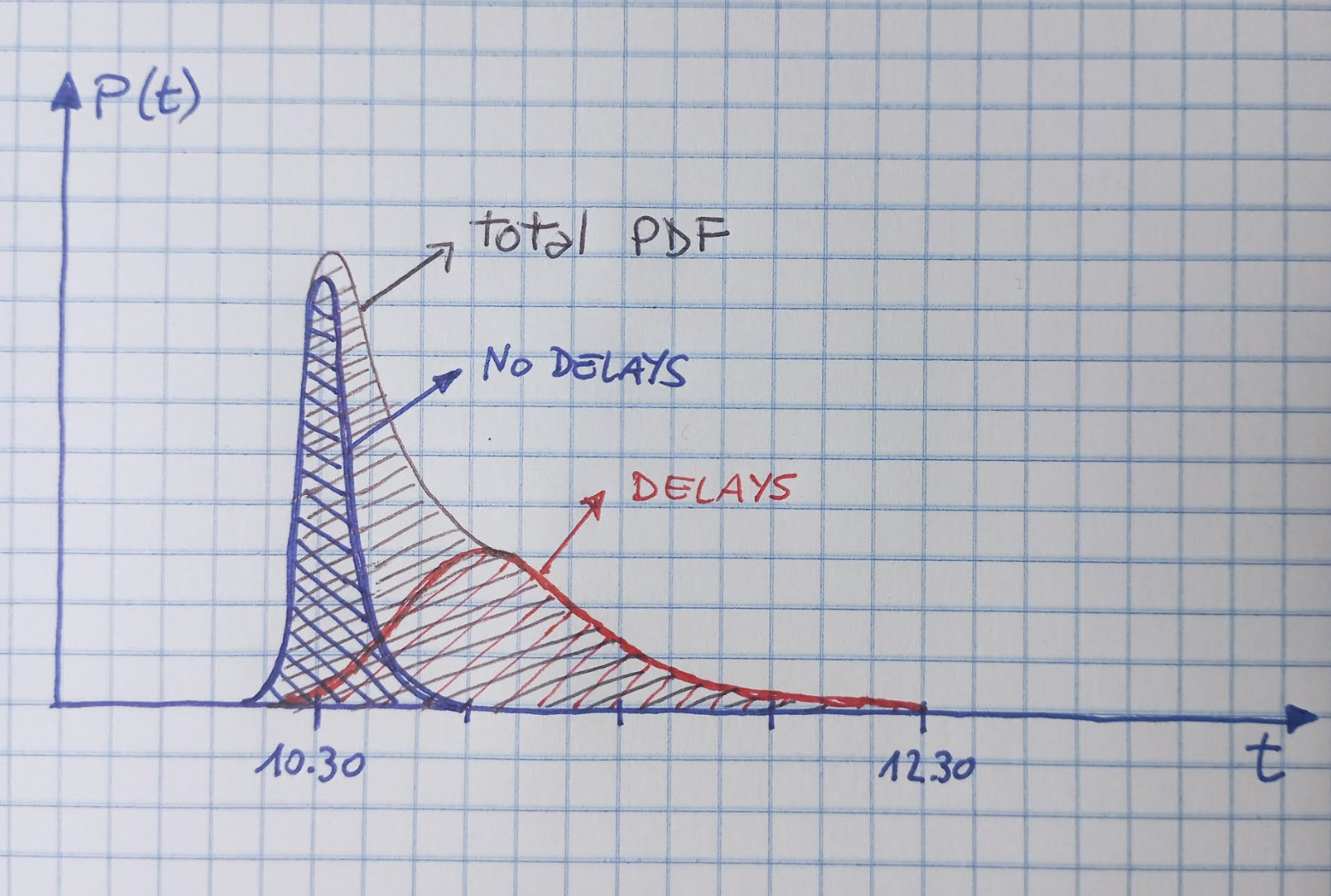
Perhaps the most important thing to get right from the start, in most statistical problems, is to understand what is the probability distribution function (PDF) of your data. If you know it exactly -something that is theoretically possible but only rarely achieved in practice- you are in statistical heaven: you can use the maximum likelihood method for parameter estimation, and you can get to understand a lot about the whole problem.
Winter is not over yet, but I am already busy fixing the details of some conferences, schools, and lectures I will give around Europe this summer. Here I wish to summarize them, in the hope of arising the interest of some of you in the relevant events I will attend to.
Pattern recognition is an altisonant name to a rather common, if complex, activity we perform countless times in our daily lives. Our brain is capable of interpreting successions of sounds, written symbols, or images almost infallibly - so much so that people like me, who have sometimes trouble to recognize a face that should be familiar, get their own disfunctionality term - in this case, prosopagnosia.
 Conferences Good And Bad, In A Profit-Driven Society
Conferences Good And Bad, In A Profit-Driven Society USERN: 10 Years Of Non-Profit Action Supporting Science Education And Research
USERN: 10 Years Of Non-Profit Action Supporting Science Education And Research Baby Steps In The Reinforcement Learning World
Baby Steps In The Reinforcement Learning World Restoring The Value Of Truth
Restoring The Value Of Truth