Natural philosophers first searched for a link between gravity and EM before the War of Independence in 1776 in a peaceful scientific discussion between the two sides. Benjamin Franklin got on a sailboat and went over to London. He talked about his experiments with electricity with Joseph Priestly. Ben had noticed there was no electric field inside a conducting cup. Priestly knew a similar thing happened inside a hollow sphere of mass. Joe jumped to the conclusion that both fundamental forces were governed by inverse square laws.
click or skip this read of the blog:
Here are the first classical field equations for gravity and EM:
 It is passé to be impressed by these relations. This picture says a few words: that I buy individualized shirts from individualizedshirts.com. It is much better to have things written on shirts than skin. I have a simplicity fetish given the Movado watch. The brightest future belongs to those who know the past the best. Know Maxwell, know physics. Know the classical field equation for gravity.
It is passé to be impressed by these relations. This picture says a few words: that I buy individualized shirts from individualizedshirts.com. It is much better to have things written on shirts than skin. I have a simplicity fetish given the Movado watch. The brightest future belongs to those who know the past the best. Know Maxwell, know physics. Know the classical field equation for gravity.Neither of these equations survives the profound message delivered by special relativity. In both cases, the fatal flaw is a change in the charge density would need to propagate instantaneously. Here is how the equations are upgraded to be consistent with special relativity:
Even to an untrained eye, the upgrade was minor for EM, but a complete break with the past for gravity. Physicist rightly beam with pride about the mathematical tour de force that general relativity represents. An untrained mind would instead guess that what is good enough for EM should be good enough for gravity:
Guessing field equations is the sport of fringe physicists. What this mini series is striving to do is drill in the right ultraconservative approach: write down the Lagrange density, plug that into Euler-Lagrange, and pick a gauge to simplify the expression. That is what I will do again, arriving at the guessed field equations for gravity, not general relativity.

The first blog derived the way to derive field equations, the Euler-Lagrange equations. The second and third blogs used quaternion multiplication in the first step, writing out the relevant Lagrange density. After that, quaternions were not used as the Euler-Lagrange machinery took over. Here are the four named Maxwell equations, eight total differential equations, written out as quaternion expressions just to irritate people who pick on quaternion nomenclature:
I like the new, lean look. Slimmer is better in the iPhone world, why not physics? Note that no new physics insights are gained ("Isomorphisms that may start a fight for $1000 Alex").
Quaternions sidebar. Since 1997, I have had a hobby of rewriting standard equations in a quaternion format at quaternions.com. This has been a great way to train in physics. Feynman wrote on his blackboard: "that which I cannot derive I do not understand". Not that my support is needed, but I agree. The vast majority of quaternionification to make up a word is mathsterbation, resulting in the same expression up to an isomorphism. The Maxwell equations remain the same, even if written differently.
Quaternions cannot do it all. I wrote up that story in a different blog about the current coupling crisis my work faced ("Shot in the Head").
The fundamental starting point for my work are tensors constrained to work in 4D spacetime: time + 3D space, energy + 3D momentum, charge + 3-current densities, changes in time + changes in space, a scalar potential phi + a 3-potential A. These can be added together, subtracted, or multiplied by a scalar. Change the coordinate system as one chooses.
There are multiple ways to multiply 4D tensors. Quaternions provide one set of rules. Those rules were used to get the Maxwell Lagrange densities. Different rules for multiplying 4D tensors are the source of variations on the Maxwell equations.
Imagine a variation on a quaternion product symbolized by a boxcross sign that banished all minus signs:
My favorite part of this rule is the symmetric cross product, symbolized by the ocross sign. No more looking at my right hand, trying to figure out which one is negative. All are positive! This re-invention of mine could go under several different aliases. It can be viewed as a form of hypercomplex numbers. I am not a big fan of the label since nothing appears hyper or complex to me. Most representations of hypercomplex numbers have a minus sign in their products. The California representation of hypercomplex numbers has much better marketing appeal, but is too long. Someone suggested California numbers. For this blog, I will shift again, talking only about California products. Starting with any pair of 4D tensors, I can form either the quaternion or California product, depending on what is needed. Math wonks will not embrace the hydra. The California product - just the product - is nothing more than the Klein 4-group in action.
The California product commutes. Division is not assured. I do know how to determine if an inverse exists. One calculates the eigenvalues of the matrix representation. If none of the eigenvalues are equal to zero, then an inverse exists. I think this observation is neat because eigenvalues play a key role in quantum mechanics. It turns out that events on the lightcone are part of those that are excluded.
The California product is not amenable to norms. All that positivity means the imaginary part always hangs around. For the norm of a complex or quaternion product, the magic of the norm is that all the numbers huddle in the real value:
No can do for the California product.
There is one more technical detail to clarify. The current coupling term needs to be invariant under a Lorentz transformation. [IMPORTANT CORRECTION: to make the force equation work, the current coupling term has to be different from what appears for the Maxwell equations. It is not invariant under a Lorentz transformation.]
[comments on conjugates deleted.]
Construct a complete set of first order changes to a spacetime potential. To create a variant on EM, this time the California product will be used.
The gauge term g is exactly the same as the one for the quaternion product EM field definitions. This detail will be essential for the last blog in this series, deriving the unified GEM equations.
Exactly half the signs showing up for what I defined as the symmetric small e and small b fields have flipped signs compared to their EM electric and magnetic field counterparts.
The Maxwell Lagrange densities required two variants of the field equations. That was accomplished by changing the order of the quaternion product. The same trick will not work with the California product that commutes. What can change is which of the two gets the conjugate.
I changed the order so I can follow the made up rule "conjugate the first one". This time it is the symmetric field small e that flips signs, not small b.
The Lagrange density must be written out its component parts. The symmetric small b field is easy now:
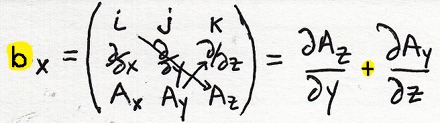
[Note: to show I am doing a variation on the Maxwell source equations, I will often use the same graphic, using a yellow highlight on the region that changes.]
The small symmetric e field requires some thought. I cannot remember why I chose to define the field this way, the decision looks arbitrary to me:
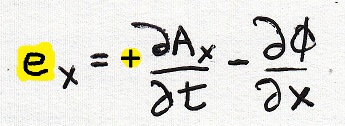
Square both fields.


Subtract and clone for y and z.
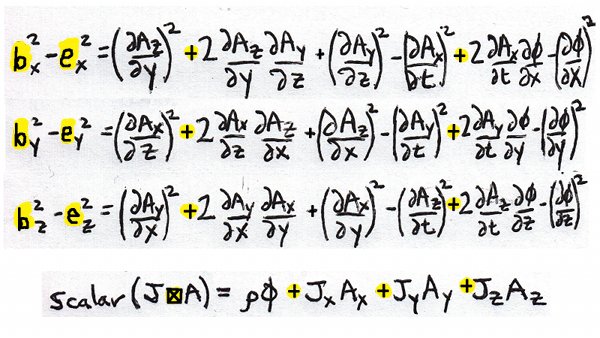
The current coupling term stays the same, while the difference of the squares of the two fields only changes signs of the cross terms.
The current coupling term and the difference of squares needs to be combined. One could take the sum or the difference. The resulting laws would be different :-) I want an equation that in the static limit will give me Newton's law of gravity. For that reason, I need the sign of the rho phi term the same as the squared phi derivatives. Here is the hypercomplex gravity Lagrange density it its component parts:
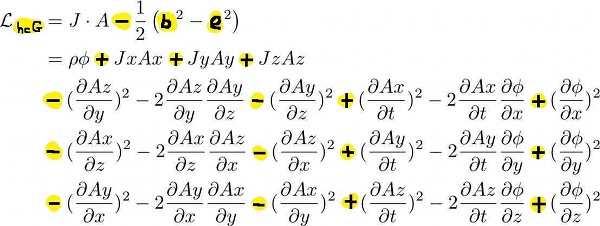
The sign flip means the mixed terms stay the same, all the squares flip. Here is the micro review of all the needed calculus:

Focus on the terms with a phi in them, over on the right: [IMPORTANT CORRECTION: the current coupling terms in the following images have all been updated as needed to make a sensible force law proposal.]

Start taking Euler-Lagrange derivatives:

We are free to pick a gauge since all the gauge terms get subtracted away. Use the Lorentz gauge:
Rewrite the equation above with this gauge choice:
This is the initial guess, but now it is not a guess, it is part of the standard way to derive field equations from a Lagrange density.
Here is the summary statement:

The calculation for the symmetric Ampere's law is darn similar. Focus on Ax terms.

Apply Euler-Lagrange:

When the hypercomplex Ampere's law is written in the Lorentz gauge, the three field equations look like so {IMPORTANT CHANGE: the current coupling term change effects these three laws]:
Half the signs are positive, the other half negative, kind of trippy.
One nice feature of the Maxwell equations in the Lorentz gauge is how simple they behave under a Lorentz boost. The current density is a 4-vector, the D'Alembertian is invariant, and the 4-potential transforms like a 4-vector. Simple is good.
The world is not always simple. Here we have the same 4-potential. The differential is not a D'Alembertian. The way the differential transforms under a boost can be calculated in a straight forward way. Whether one can find a pithy way to describe the process is a different issue. The current density J must give away clues that spin 2 particles mediate this force. I do have a blog devoted to showing the current coupling term using the hypercomplex product has spin 2 symmetry, necessary for like charges to attract. For those that want to see that these field equations are consistent with current tests of weak field gravity via a solution that generates the exponential or Rosen metric, that was covered in a different blog.
Here is the summary statement:
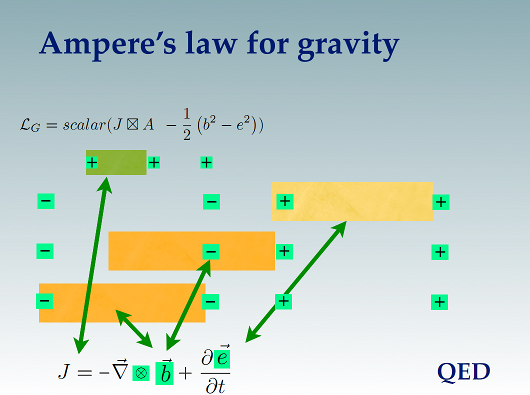
And a comparison between the hypercomplex Gauss's and Ampere's laws:
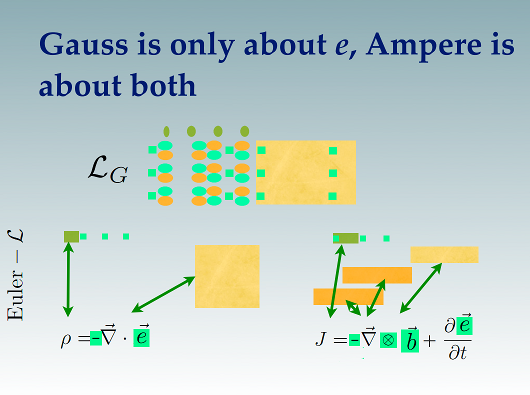
There is no vector identity I can spot using the California product. All those positive signs means there is no way to cancel things out. This is very good news. We all have extensive experience with gravitational monopoles like the Earth.
Gravity only knows how to attract. The California product does not know a minus sign. Sounds like the two were made for each other.
Doug
Snarky puzzle. Show that b2 - e2 is [correction: not] invariant under a Lorentz boost. I am pretty sure I did that calculation once.
Google+ hangout: 11:00-11:45pm Eastern time, Tuesday-Friday. http://gplus.to/sweetser
This could be an efficient way to exchange a few ideas. If you have a question or two, hangout.
Bet against the Higgs being found, buy the t-shirt
Next Monday/Tuesday: Derive the GEM Unified Field Equation (5/5)



Comments