So let us see what these results are. Before we do, though, let me give some sort of an introduction in the kind of science the CMS experiment does. CMS stands for "compact muon solenoid", but also for "continuous meeting system". I am joking, of course, but the fact that you as a member of the experiment can spend a life sitting in meetings from 8.30 in the morning to late night every day is no fiction.
Two words about the CMS detector
The CMS detector is constructed inside and around a large cylindrical magnet built with superconductor materials, and capable of a uniform 3.8-Tesla field in its interior. Such a very strong magnetic field allows to bend the trajectory of charged particles produced in the proton-proton collisions that take place in its center, and from that bending, detected by the ionization trails the particle leave behind, physicists can precisely infer the energy of the particles. That "trail" is in truth a set of localized ionization deposit left in thin and precisely read out silicon detectors.
Another method that CMS uses to measure the energy of subnuclear particles is by letting them hit heavy nuclei inside detectors called "calorimeters". This process generates secondary particles and eventually a shower of secondaries that overall betrays the total energy of the initiator.
Outside the magnet, CMS is endowed with a very effective set of muon detectors, that are tasked with measuring the trajectory of these particles. Muons are heavier replicas of electrons, and they are very important to measure well - they provided important discoveries in the past, including the W and Z bosons, the Upsilon mesons, and the top quark and Higgs boson. They are practically the only kind of particles that we can observe outside of the CMS solenoid, as all others are stopped in the calorimeters or are invisible to us (the neutrinos).
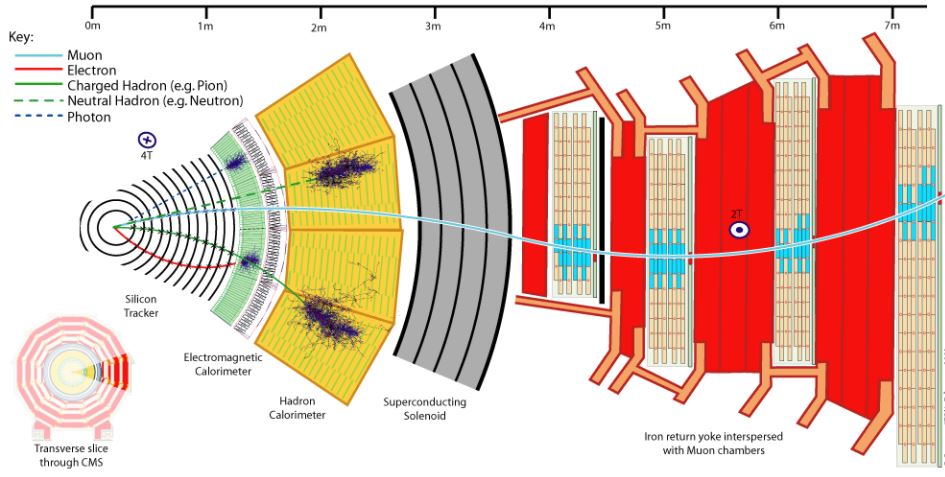
Above: a cut-away view of a sector of the CMS detector, showing the various subdetectors and the signals that different particles leave in them.
The detector system collects information on all produced particles during the proton-proton collisions, that take place 40 million times per second in the core of the detector. Since the resulting amount of data is impossible to store, a trigger system selects the 1000 collisions per second that are most interesting, and saves them to magnetic support, discarding all others. This is not a waste of potential discoveries, as proton-proton collisions are for the largest part un-interesting. Only the most energetic ones are worth studying in detail!
The experiment has collected a large amount of data in the past few years, a period of data taking of the Large Hadron Collider called "Run 2", which delivered about twenty quadrillion collisions overall to CMS. As we said, though, only some hundred billions of them -the most interesting ones- were collected by the trigger system. That's enough to make data analysts happy and keep them busy for a long time!
The two signals
The two signals we are discussing today are very different. The first one is constituted by the production of a Higgs boson with the subsequent (immediate) decay of the Higgs into a Z boson and a photon. Such a process is exquisitely interesting for a physicist, because we are talking of three bosons, each one carrying a different force of nature, linked to one another in a very rare and peculiar process. The Higgs boson does not couple to photons directly, as it is only sensitive to particles by virtue of the mass of the latter, and the photon does not have a mass. On the other hand, the photon does not couple to Z bosons and to Higgs bosons because neither of those particles has an electric charge! So how does the decay of a Higgs to a photon and a Z boson take place?
The answer is that it is a "loop diagram": something that is intrinsically quantum mechanical. The Higgs boson "emits" a quark pair, e.g., and the quark pair dissolves as it was created, but before doing so it emits the Z and the photon. The same trick can be pulled off by a pair of W bosons, as the W's, like quarks, possess an electric charge (coupling to the photon) and also couple to the Z boson. The three main Feynman diagrams that describe these reactions are shown below, and should be read from left to right: "A Higgs boson comes by, it emits a pair of W bosons," (in the top graph, e.g.), " and the W bosons then disappear, leaving behind a Z and a photon". The "f" in the second diagram on the bottom left is instead a fermion of any kind - a quark or a lepton; but in truth, the only relevant fermion for this particular process is the top quark, as all other fermions have too low masses in comparison, and the probability that they contribute is consequently far smaller.

The trick of a loop diagram for a decay costs the Higgs in terms of probability: it is a rare process, because it involves summoning out of the vacuum this virtual pair of intermediate particles. The rarity means that we have to collect a large number of Higgs decays (so, large datasets) to search for the process we are interested in - only one in a thousand, or less, will do that trick.
Fortunately, the CMS detector sees photons very well, thanks to the electromagnetic showers that the photons produce in its calorimeter. As for the Z particle, it immediately decays to a pair of electrons or muons (seven percent of the time), making itself visible in the calorimeter or in the muon chambers, respectively. But processes that look like a Higgs decay to Z and photon abound, so the search is background-ridden, and we can only prove that the decay is present in the data by statistical means, involving the reconstruction of the total mass of the photon plus Z system and the observation of a peak at 125 GeV - the mass of the Higgs boson. You can see the result of this mass reconstruction in the graph below.
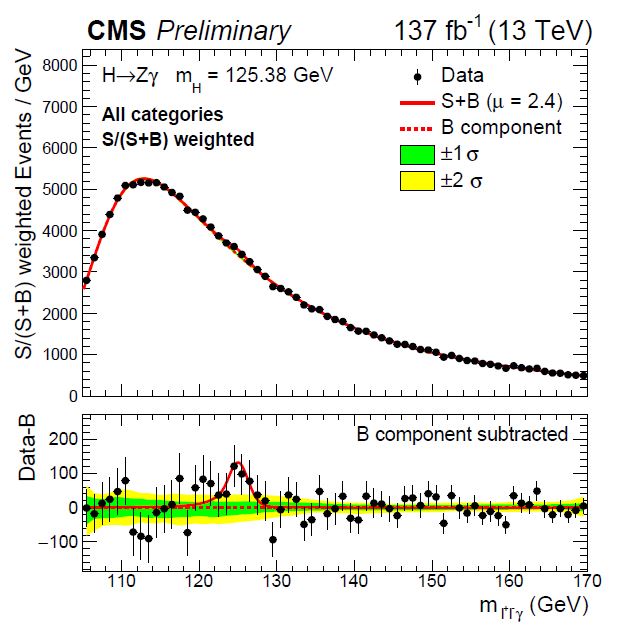
In the top panel you see the distribution of the selected data - events that all contain a clean Z signal and a energetic photon candidate. The signal is too small to be visible in there, but if we subtract off the background, which is predicted by a smooth function, we get the graph on the bottom, which shows the data dancing up and down with respect to the line at zero - which corresponds to conforming to the background hypothesis. At 125 GeV, though, there is an excess with a nice Gaussian shape, which is most likely due to real decays of a Higgs to a Z and a photon!
The graph, to tell the truth, is the result of combining several different sub-datasets together - not only Z decays to electrons or muons, but also many combinations of photon signals of different purity. By giving a weight to events in proportion to their signal purity, it is possible to have a view at the data which more closely conveys the statistical power it has in discriminating the signal by a complex statistical analysis.
So the signal you see above has a significance of 2.7 standard deviations - a roughly "few in a thousand" kind of effect. Typically such evidence is insufficient for physicists to claim to have observed a phenomenon; they usually require 5 standard deviations for that. On the other hand, there is in this case very little doubt about its genuine nature. The reason why we can be sure with much fewer "sigmas" than the convention is that the convention is built to prevent false claims due to having looked for a signal in a number of different places, thus boosting the probability of one significant observation. This "Look Elsewhere Effect" is absent in the search here described.
The second signal: new physics in multi-jet events?
The other analysis I wish to talk about here is a search for massive new particles that decay to pairs of hadronic jets. Since a hadronic jet (a collimated stream of hadrons) is the most frequent thing you can see when you collide energetic protons, when a quark or gluon ejected with high energy from the collision point materializes in a spray of hadrons (protons, pions, kaons, and other particles we can detect in tracker and calorimeters), the signature of a new particle decaying to two jets is not simple to extract from those huge background processes.
One possibility to make the search easier is to rely on a specific model which supposes that a massive particle X is created in the proton-proton collision, and this decays into two lighter particles Y, which subsequently produce a pair of hadronic jets each. What one would then observe in the detector would be four well-separated jets, all very energetic (if the mass of X were large, e.g.). Something like the signature of the event display below:
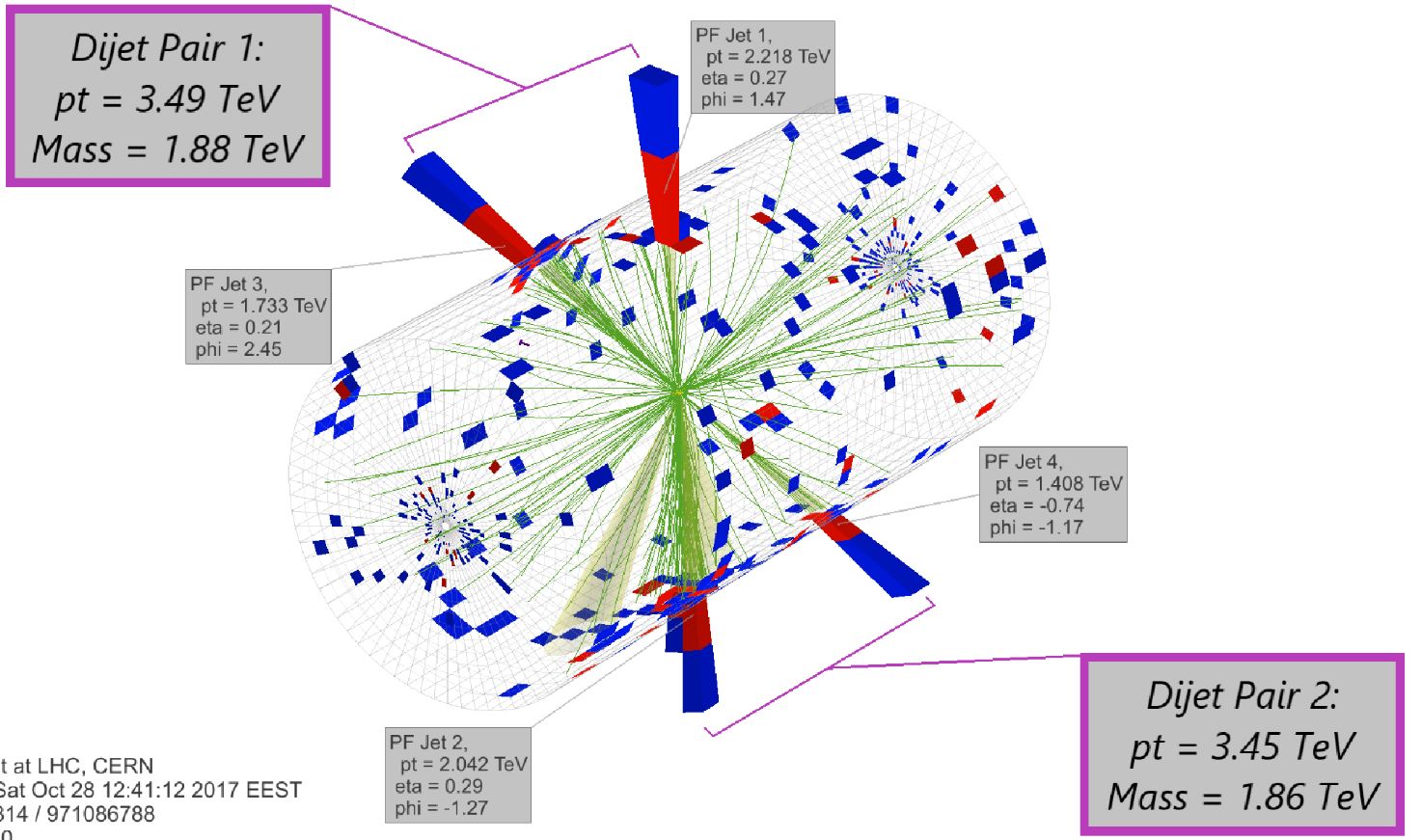
The above event is a spectacular four-jet event that was effectively observed in CMS data. And the fact that the four jets make a "X" is suggestive, is it not? As Indiana Jones taught us, however, the X in the map never marks the presence of the treasure. Or maybe sometimes it does?

Anyway, the CMS search carefully considered ways to enhance the observability of the considered signature, and produced a precise background model to interpret the data and put a small signal in evidence. Since previous searches had ruled out the presence of that kind of new physics, if the mass of the X particle was below a certain threshold, the interest of the present search was focused on very high-mass events, which smaller datasets could not be sensitive to.
The result of the search may be summarized in two ways. One is the reconstructed mass distribution of X particle candidates, which shows a trickle of very high-mass events at the right end of the spectrum (up to 8 TeV!). A background model overlaid to the data shows that in general the observed data is well in agreement to the "no signal" hypothesis. But those high-mass events are suggestive...
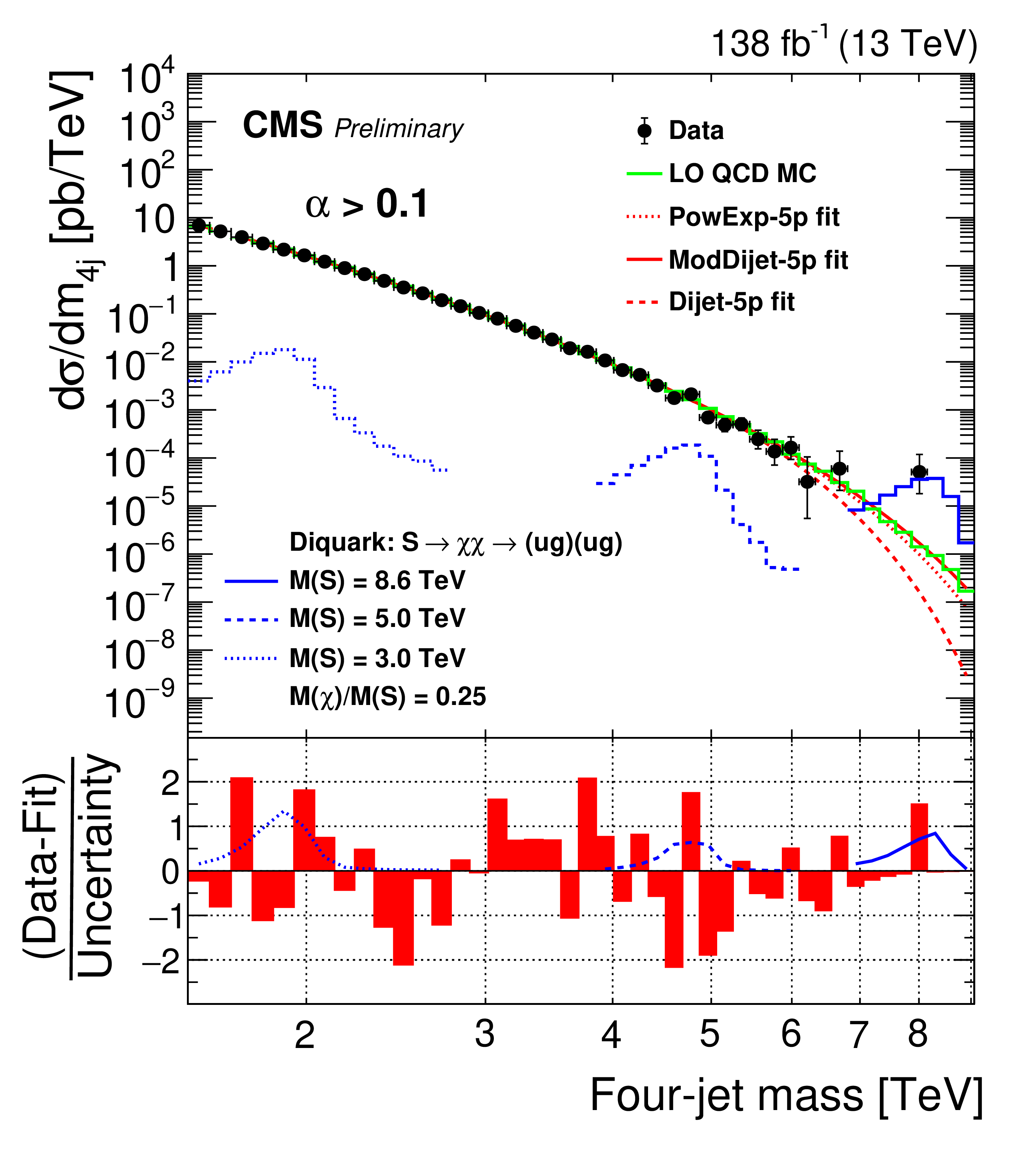
Above, the top panel shows the data (black points) and a few background models (red curves), together with the expected shape of a signal at various masses (in blue). The lower panel shows that the deviations of data from the model is not too significant anywhere in the spectrum.
The other summary of the data is a so-called "p-value" plot. Here, as a function of the hypothetical X particle mass, one plots the probability of obtaining data at least as discrepant with the background-only hypothesis as those observed. Such is a "local p-value", because the plot summarizes what statisticians call "multiple testing": if you have a parameter that describes all possible alternative theories (the mass of the new particle), you are searching in a number of different places and thus your p-value is bound to become low somewhere, just because of random fluctuations. What counts is the "look-elsewhere-corrected", "global p-value" that corrects for that multiplicity. You can see the difference between the two p-values by comparing the two vertical axes on the right and on the left of the plot below. Note that CMS is naming Y the high-mass particle, and X the two products - I preferred to keep X as the high-mass object's name in the discussion above.
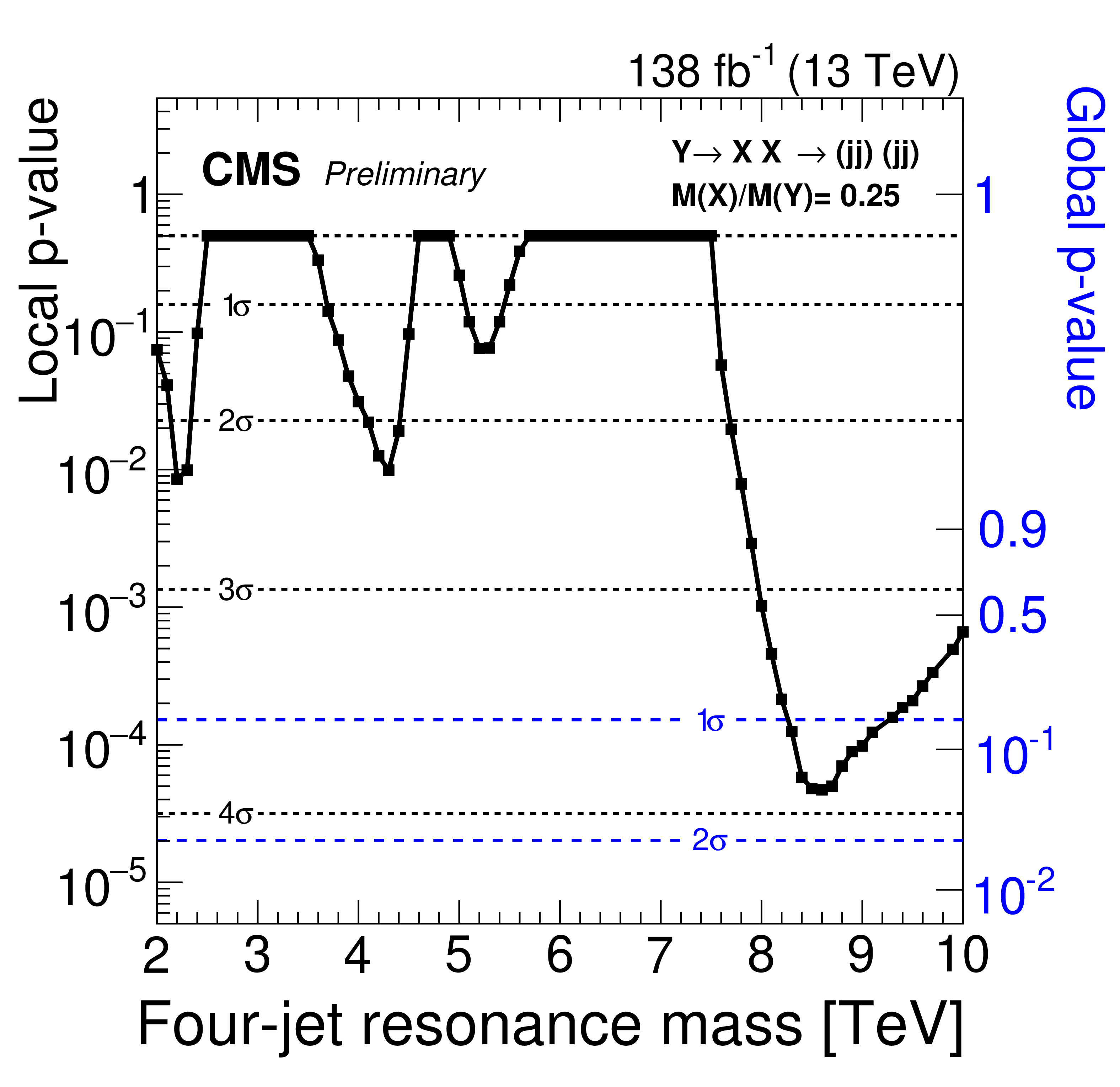
So what we get to see is that we have an excess of almost 4-sigma local significance (left axis), which once corrected for the multiplicity of searches becomes a less than 2 sigma effect in this case. Still, a very suggestive small bounty of very energetic collisions! It would be fantastic if this became a true new physics signal, but as you can imagine, of the two signals discussed in this post, the first is going to grow with the data, and the second is going to instead be reabsorbed, as background fluctuations do.
---
Tommaso Dorigo (see his personal web page here) is an experimental particle physicist who works for the INFN and the University of Padova, and collaborates with the CMS experiment at the CERN LHC. He coordinates the MODE Collaboration, a group of physicists and computer scientists from eight institutions in Europe and the US who aim to enable end-to-end optimization of detector design with differentiable programming. Dorigo is an editor of the journals Reviews in Physics and Physics Open. In 2016 Dorigo published the book "Anomaly! Collider Physics and the Quest for New Phenomena at Fermilab", an insider view of the sociology of big particle physics experiments. You can get a copy of the book on Amazon, or contact him to get a free pdf copy if you have limited financial means.






Comments