Hadrons are composite particles made of quarks. The word "hadron" comes from ancient Greek αδρος, which means "thick, bulky". The two hadrons we know best are protons and neutrons, which make up atomic nuclei; but there exist literally hundreds more, which are unstable and decay very quickly after they are created, in subnuclear reactions we can produce using particle accelerators.
During the 1940s and 1950s scores of new hadrons, each with its own different properties (mass, spin, lifetime) were discovered by converting the kinetic energy of accelerated protons into new matter states, leveraging Einstein's famous formula "E=mc^2" which indeed describes the mass of bodies as one form of energy, into which other forms of energy may duly be converted. The complicated taxonomy of hadrons was simplified in the early 1960s by a few physicists, most notably Murray Gell-Mann and George Zweig, who understood that all observed hadron states could be explained as combinations of three constituent quarks, as Gell-Mann named them, or quark-antiquark pairs.
The fact that you can combine three quarks (up, down and strange, identified by the letters u, d, s) or quark-antiquark pairs to form composite particles of measurable properties calls in a mathematical structure that handles the combinations, and describes the symmetry properties of the composite particles. This is a group of symmetry, which for three quarks is SU(3). I will not discuss the detailed properties of the "special unitary" SU(3) group here (you can find many online sources for that purpose. Instead, I will try to explain how to construct hadrons from quarks, and make it fun if possible.
We start with describing a couple of important properties of the quarks: they have electric charge Q and strangeness S. Q and S are additive quantities, so if you combine three quarks of charges Q1, Q2, and Q3, the composite hadron will have total charge equal to the sum of the three Q's. The same goes for strangemess. Here are charges and strangeness of the three building blocks:
- u: charge Q=+2/3, strangeness S=0;
- d: charge Q=-1/3, strangeness S=0;
- s: charge Q=-1/3, strangeness S=-1.
Knowing that, what do you get if you combine two up quarks with a down quark? The answer is that you get a hadron with quark composition (uud), with total charge Q=2/3+2/3-1/3= +1, and strangeness S=0. Such a particle is the proton. Similarly, if you combine two down quarks and an up quark, what you get is a hadron (udd), with charge Q=2/3-1/3-1/3=0, and again S=0. That is a neutron.
It was discovered in the first half of the 20th century that many radioactive phenomena of unstable elements could be explained by the transmutation of a neutron into a proton, with the emission of "beta radiation" - what we soon identified as an energetic electron - and an electron antineutrino (the understanding that an antineutrino was also involved in the decay took some time to take shape). In terms of quarks, the reaction can now be more easily understood as the transmutation of a down quark into an up quark, by the action of a force called "weak interaction". We know today that the process involves the emission of a W boson, whch then turns into an electron-antineutrino pair. But I am divagating, so let's go back to quarks.
So, let us introduce a thing called "weight diagram". This is a diagram on a plane where the horizontal axis describes the charge of bodies, and the vertical one the strangeness. On such a plane, the three quarks can be arranged in a triangle as shown below:
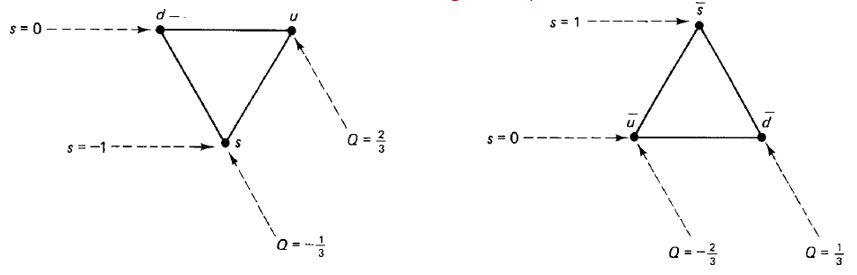
Antiquarks, which have opposite charge and strangeness to the corresponding quarks, can similarly be arranged in a triangle with opposite orientation, as shown on the right above.
What to do with these diagrams? They allow us to combine quarks into hadrons of different symmetry properties. The symmetry we are talking about here is one which explicitates in the phenomenology of hadrons as subjected to the strong interaction - the interaction that keeps atomic nuclei together. Quarks feel the strong interaction and bind themselves into triplets or body-antibody pairs because of the action of that force. And the strong interaction cannot distinguish the species of quarks it acts upon: for the strong interaction, all quarks are equal. So in terms of the strong interaction, a proton and a neutron are exactly the same thing: there is, therefore, a symmetry property of all systems made up of protons and neutrons, in the sense that if you exchange a neutron with a proton nothing changes as far as the strong force is concerned. This has important consequences for the stability of nuclear matter.
There are a few rules that govern the combination of weight diagrams. Here they are:
1) The obtained diagrams will have exagonal symmetry (more than a rule, this is an observation);
2) Every site at the boundary and inside the diagram, at the intersection of weight diagrams, is occupied by a state;
3) The number of such states at the boundary is one, and the multiplicity grows by one progressively as we move inside the diagram.
The above sounds a bit abstract, so let us put it to the test. Let us use the weight diagrams to create a "meson" - a hadron made up by a quark-antiquark pair. We can do this by the group operation of combining a 3 representation with a 3-bar one. In practice, we overlay a 3-bar weight diagram on top of each vertex of the elements of the 3 weight diagram, as shown below:

As you see, since 3 by 3 is nine, we have created nine states (second row in the figure above). By the rule that demands a multiplicity of two in the center of the exagon, we know that we have to divide this "nonet" of states into an octet and a singlet, as shown in the bottom row.
If we now read out the quark-antiquark composition of the states we have produced, we identify states that correspond to physically known hadrons: for isntance, we have the positive and neutral kaons on the top row, the three pions in the central row, the eta particle at the center, and the antiparticles of positive and neutral kaon at the bottom row.
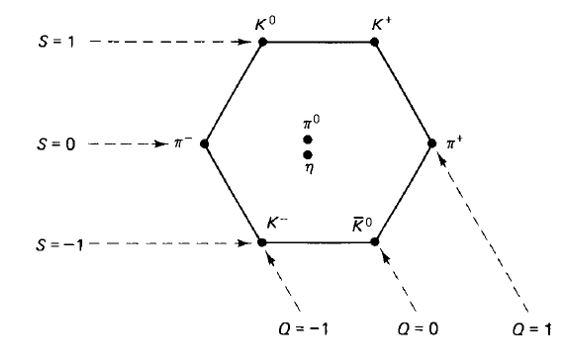
In terms of group mathematics, we have found a decomposition of the 3 x 3-bar into 8 + 1. The eight states of the octet possess the same symmetry with respect to the strong interaction: they are completely equivalent states as far as that interaction is concerned. If they are produced with different rates in particle collisions mediated by the strong interaction this is only due to their different mass, which causes some reactions to be more probable because of energy conservation considerations.
There is another thing that I should mention about these multiplets: all elements in them have the same value of another intrinsic attribute of elementary particles - the quantity called "spin". The above octet, for instance, is made up by mesons that all have spin=0. You can get a spin-zero meson by combining quarks, which have spin 1/2, if the two quarks arrange their spins to be antiparallel to one another. But you can also combine quark-antiquark pairs into mesons with spin 1, if the two quark spins are aligned: these are called "vector mesons" and they are part of a different octet.
Things get more interesting if we set out to construct baryons - particles made of three quarks such as the proton and the neutron. When Gell-Mann and Zweig had their epiphany, scores of baryons heavier than the proton were known: the delta particles, formed by a quadruplet of states of similar mass and properties, and with charge +2, +1, 0, and -1; the sigmas, a triplet of still heavier states of strangeness -1 and charges -1,0, and 1; the xi minus and the neutral xi baryon, still heavier and with strangeness -2. Let us see how to arrange them in a supermultplet by using the combination rules of SU(3).
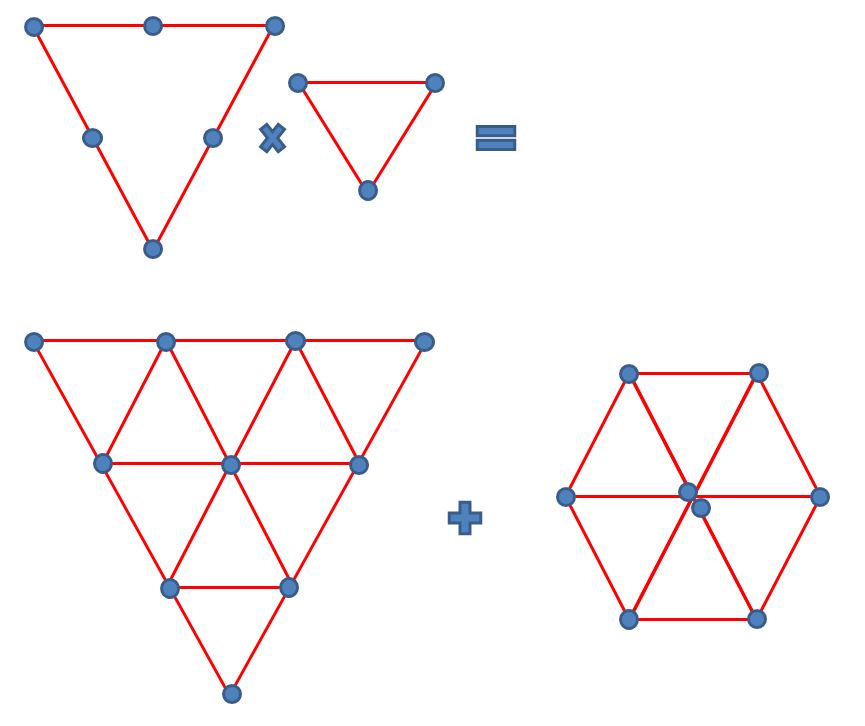
We start with the weight diagram describing the "3" representation, and create a 3x3 configuration by overlaying a second "3" triangle on top of each vertex of the first one. If we check the rules of combination of weight diagrams, we see that we have constructed a sextet and an inverted triplet: 3x3 = 6 + 3-bar. With that, we have created "diquark" combinations, which however do not correspond to physical states (they would be "exotic" hadrons, which however cannot exist as bound states because of the properties of the strong interaction - matter for another post). So let's continue and create the combined weight diagram for 3x3x3. First, let me show you the maths of it.
3x3x3 = 3x (6+3-bar) = 3x6 + 3x3-bar = 10+8+8+1
As we can see, the 3x6=18 reduces to a decuplet and an octet because of the rules of weight diagrams - check it out in the figure below. Then, 3 x 3-bar is 8+1 as seen before. Read this way, by combining three quarks we get a totally symmetric decuplet of states, two octets of mixed symmetry, and a totally antisymmetric singlet. Below are the weight diagrams decompositions.
The decuplet we have constructed is made up of 10 baryons including the delta states, the sigma-stars, the xi-stars, and the omega minus particle. These particles possess respectively zero, minus one, minus 2, and minus 3 strangeness, and all have spin equal to 3/2 - they are thus totally symmetric with respect to the exchange of a quark with another, as far as the strong interaction is concerned. See the assignment of states to the vertices below:
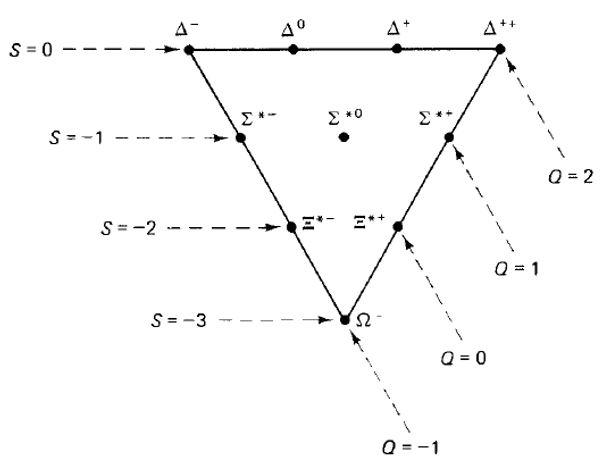
In terms of quark composition, the delta++ is made up by three up quarks; the delta minus, at the top left vertex, is a (ddd) combination; the omega minus is a (sss) combination. In-between, you find states made up by other combinations of the three quarks.
Fun, isn't it? Well, ok, fun for geeks, but you cannot deny that the mechanics of combination of quarks into hadrons studied with the rules of composition of SU(3) representations has some charm. Charm, by the way, is the name of the fourth quark, and if you introduce it in the scheme we need to enlarge the group SU(3) to SU(4), and weight diagrams become three-dimensional, making the picture much more complex in graphical terms, if still trivial from a mathematical point of view.
I should also mention that there is a different way to make calculations with SU(3) representations (or others, for that matter), based on what is called "Young diagrams". Those are a lot of "fun", too, but they belong to another post, given the length this one has already taken....





Comments