The talk was titled "Quarkonium and heavy quark production in pp collisions" and focused on the results produced by the CMS experiment on 2010 proton-proton collision data delivered by the Large Hadron Collider, CERN's "end of the world" machine. I discussed six experimental results that have been produced with a fraction of the total data currently available to CMS: all the measurements are in the process of being updated with the full statistics collected in 2010, so improved results are to be expected in the forthcoming weeks. Nonetheless, the comparisons of existing results with theory predictions provide an interesting picture of our understanding of the production of heavy quarks in hadron collisions.
In the following I will try to give just a few highlights of the results, providing explanation to the general concepts, but I am not going to be able to delve deep into the rich phenomenological issues that are interested by these measurements. My apologies for that, but you can always use the comments thread to set up some interesting follow-up discussion of details I am not covering here. Since this post would otherwise be too long, I decided to cut it in two parts: in the following I provide a general introduction, and in the second part, to be published in a few days, I will offer some of the results. As an anticipation, however, let me post straight away the conclusion slide from my talk. If what is written below does not make any sense to you, worry not: read the text below and come back for more details on the results in a few days!
And now, the introductory information.
Two words for the layman
Let me start by explaining why the production of charm and bottom quarks is interesting. These quarks are collectively called "heavy flavour" since their mass is significantly heavier than that of other quarks. Charm weighs about 1.2 GeV (about twenty times more than the strange quark, and over two hundred times more than the up and down quarks), and bottom weighs about 4.8 GeV. The top quark, still forty times heavier than the bottom quark, has been excluded in the last two decades by this classification because its properties make it unique (I do remember, however, sitting in "heavy flavour group" meetings in CDF in the early nineties, when top quark physics was discussed together with that of bottom and charm!).
What does the heavy mass provide ? Why are these quarks singled out ? The heavy mass provides a natural cut-off from the hard-to-model, impossible-to-calculate low-energy phenomena that quantum chromodynamical (QCD) interactions produce in hadron collisions. It is as if by considering the production of these quarks one can neglect the part of QCD which we cannot calculate. The reason why at low energy we have a problem with QCD is that the strong coupling constant -the number that multiplies all reaction rates a number of times equal to the number of vertices of the corresponding diagrams- is a decreasing function of the energy at which an interaction occurs. Let me explain better.
If a reaction between quarks or gluons occurs at an energy of 100 GeV, say, the strong coupling constant which applies to the calculation of the process has a value close to 0.1. This means that the process can be calculated by what is called a "perturbative expansion" in powers of that coupling constant. The square of the strong coupling constant is 0.01, and the third power is 0.001: this guarantees that the consideration of "higher-order processes" (ones which contain more vertices in the diagrams which describe them, and thus which must be multiplied by powers of the coupling constant) produces only small corrections to the lowest-order result. The theoretical calculation converges, and the result is meaningful.
If, instead, the reaction occurs at an energy of 1 GeV, the strong coupling constant there has a value of 0.4 or so (apologies for the approximations I use here, for didactical purposes). Higher powers of the strong coupling constant are not so small, and the calculation becomes unreliable. QCD becomes hard to test at low energy.
Now take a bottom quark. It can be produced in pairs by a hadronic collision. The energy of the collision which produces a bottom-antibottom pair cannot be smaller than twice the bottom quark mass, lest energy conservation prevents the materialization of the pair. So the process occurs at energies where the strong coupling constant is small enough that perturbative QCD calculations can be carried out with sufficient precision.
The "bottom" line (apologies for the confusion!) is that the production of charm and bottom quarks can be reliably calculated and compared with experimental results. But there is another side of the coin: experimentally, charm and bottom quarks are easy to single out, because they produce a rich phenomenology. Both charm and bottom quarks create mesons that live long enough to be spotted when they eventually decay, yielding so-called "secondary vertices".
Basically what happens is that a B meson (a bound state of a bottom quark and a light quark) is created by the proton-proton collision, and then travels away from the interaction point, living about one and a half picoseconds (D mesons, containing a charm quark, live three times less, but the same considerations apply). A picosecond is a really short time for us -it is a thousandth of a billionth of a second!, but it is enough for the B meson to travel some millimeters. When the particle eventually disintegrates into a few lighter particles, we can detect it from the fact that its decay products do not appear to originate from the interaction point, but away from it.
By reconstructing the decay vertex of B mesons, we can single these particles out. We can then count how many such particles are produced, and compare this with the theoretical predictions. We often do it as a function of the energy that the particles are seen to be carrying away from the interaction point, or as a function of the angle that their flight direction makes with respect to the beam line. This provides more information to compare theory and experiment, and allows us to improve our understanding of the production mechanisms and of the theory of strong interactions.
And what about quarkonium ?
Quarkonium is a bound state of a quark and an antiquark of the same flavour, such that the net flavour content is "hidden". While a B meson has a "bottom" quantum number of plus or minus one (depending whether it contains a bottom or an antibottom quark), a bound state of a bottom and an antibottom quark, called a Upsilon meson, has zero net bottom quantum number.
The interest of quarkonium resides in its ill-understood production in hadron collisions. Twenty years ago the Tevatron data (proton-antiproton collisions at 1.8 TeV of centre-of-mass energy) showed a rate of production of charmonium (charm-anticharm pairs) which was two full orders of magnitude above the then available theoretical calculations. Two orders of magnitude! This set theorists into a frenzy to try and figure out what was going on.
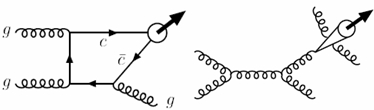A tentative answer was soon produced. Until then, the mechanism by which a pair of charm quarks bound together into a J/psi meson (the most probable resulting particle, the one which was discovered in 1974 at SLAC and Brookhaven, providing the demonstration of the existence of quarks and granting five Nobel prizes all at once) was understood to be the combination of two processes, shown on the right. Basically, the charm and anticharm quarks were produced in what is called a "colour singlet" configuration, and they then bound together into a colourless hadron, the J/psi. [The diagrams show curly lines to describe the propagation of gluons, and straight lines to show the propagation of quarks. Time flows from the left to the right. The collision of the two lines coming from the left produces the result coming out on the right. The bound state -the J/psi- is produced by the coming together of the quark-antiquark pair. It is symbolized by a thick outgoing arrow.]
Wait a moment -I think I heard somebody say-, What is a colour-singlet configuration ? Well, you may know that quarks carry a quantum number called "colour". There are three colours (red, green, and blue), that constitute the charges of the strong interaction. Bound states of quarks must be colourless: this can be achieved by putting together a red quark and a anti-red antiquark, for instance. The production of J/psi mesons by colour singlet processes assumed that the pair was first produced with the right colour-anticolour quantum numbers, and then it naturally bound into the meson.
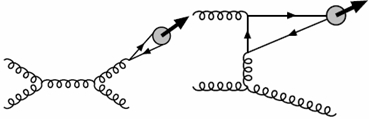The data suggested otherwise. It became clear that the quark-antiquark pair could be created in a "colour-octet" configuration as well (say, a red charm and a anti-blue anti-charm), and then it could bind into a meson by "spitting out" the unwanted extra colour (in the above case, a red-antiblue combination), in the form of a low-energy, coloured gluon. The corresponding diagrams are shown on the right.The inclusion of colour-octet diagrams solved the riddle of huge production of charmonium at the Tevatron in the nineties, and a new theoretical formalism, called "non-relativistic QCD", was developed to calculate the production properties of charmonium accounting for colour octet production and for the particular kinematical characteristics of the processes. More recently, however, a re-evaluation of colour-singlet production has demonstrated that this is all it takes to explain the production of charmonium, at least for low-energy production, and that colour-octet production is not as important as it was previously thought.
The picture is thus not altogether very clear. Experimental input is very important in the production of charmonium and bottomonium, and the new CMS data provides valuable new information at a collision energy not investigated in the past.
(To be continued)
Comments