As of late we have been scratching the barrel of "straightforward" measurements of the properties of the Higgs boson, the particle discovered in 2012 by the Large Hadron Collider ATLAS and CMS experiments. But the one property determined in the measurement published yesterday by the CMS experiment was one that many of us were very interested to check.

If a particle is an elementary body, how many individual, distinct properties can it really have? For the word "elementary" means that it is intrinsically simple! But things are not so clear-cut in the subnuclear world. An elementary particle, while devoid of inner structure and dimensions, still has a number of measurable attributes. For the Higgs boson we may size up:

- mass (of course!)
- spin (it is zero, but we want to check!)
- electric charge (it is zero, duh)
- colour charge (also zero)
- lifetime (although fantastically short, it is three orders of magnitude longer than the lifetime of the top quark)
- rate of production in association with other particles. While this is not an intrinsic property, it is connected to the particle interaction strength with other standard model particles
- rate of decay into different final state particles. This, too, is an observable feature connected with the interaction strength.

The latter two features are in truth a combination of a number of observable, measurable properties. So, e.g., the Higgs boson may decay to pairs of photons, or pairs of Z bosons, or pairs of W bosons, or pairs of b-quark pairs, or pairs of muons, etcetera... And each of these possibilities has its own associated relative probability. To measure each we have to do entirely different analyses. And since some of them are very, very small and so the related processes are quite rare, they constitute a challenging task.

For the Higgs boson, which is a hot topic in collider physics because of its possible connections to new phenomena we haven't yet observed (new physics beyond the standard model), the amount of effort deployed to measure the above quantities has been huge. ATLAS and CMS, which are each constituted by over 3000 researchers, have devoted a significant fraction of their resources in that investigation program. So we know well the higgs mass, we know that its spin and charges are zero, and we know with good precision the rate of decay to the most frequent final states. But that, until yesterday, did not include the rate of decay to muon pairs.

The reason why the Higgs decay to muon pairs is hard to measure is that it is quite rare: if you take a thousand Higgs bosons, less than one of them will on average decay into a pair of muons. So collecting large statistics of proton-proton collision was necessary to pull off that measurement. But then, the precision of the reconstruction of the momentum of those two muons also played an important role, as the better you measure the decay products four-momenta, the more precise becomes the estimate of the decaying particle's mass. And that is the key to seeing the decay and sizing it up.

In the plot below you see the mass distribution of pairs of muons observed by CMS after a data selection tuned to the characteristics expected for Higgs production and decay to muons. As you can see, the histogram shows a smooth exponential decay toward larger masses. It is mostly background - only a very tiny fraction of the collected events are the result of Higgs decays. But those few events pile up at the correct mass - near 125 GeV. That is what makes the process distinguishable, thanks to the intrinsic attribute -mass- that the Higgs possesses.



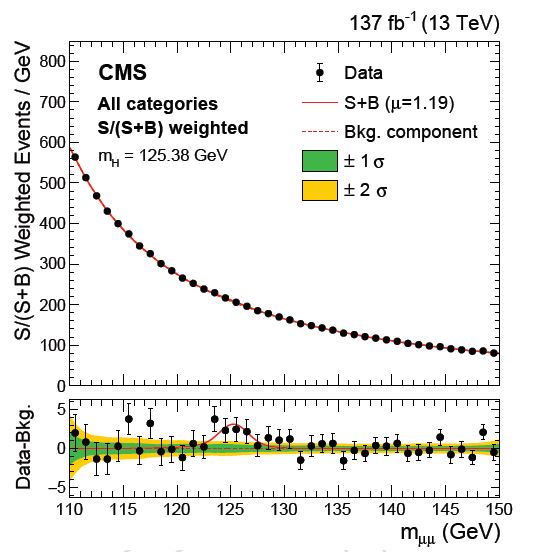
ATLAS also produced a search for the same process, but they have a slightly less performant measuring system for the four-momentum of muons, which turns into a lower mass resolution for the H->μμ process. Hence they did not observe as significant a signal peak as CMS did. Their data, however, is a nice confirmation of the CMS observation. In terms of statistical significance of the observed effects, the ATLAS result stands at about two standard deviations (a one-in-fortyfive chance that they should see the observed effect if no Higgs boson were contributing); the CMS result stands at three standard deviations, so as a one-in-seven-hundred chance of the same, so it is at the level of solid evidence.

As some of you know, particle physics experiments have this convention of requiring five standard deviations to be able to claim to have "observed" a physical phenomenon. This convention goes back to 1968, when people were looking for new particle signals in hundreds of different ways - the strictness of the significance requirement was a way to avoid incorrect claims due to sheer statistical fluctuation, due to the multiple testing that was going on. This is still a valid prescription today, but in the case of the search for a known particle, of known mass, it makes very, very little sense to argue that five sigma should be required - CMS only looked in one place, not hundreds, and found what it was supposed to find: a small but significant signal of Higgs decays, peaking at the expected mass.

Because of the above, it is perfectly legitimate, in my opinion, to give proper value to the measurement of the Higgs decay rate that CMS extracts: this is found to be 1.2+-0.4 times the expected value if the standard model is correct - which means that the standard model rulez!

Due congratulations to the CMS and ATLAS teams for pulling off these challenging results!