When subnuclear particles traverse matter they give rise to a multitude of physical phenomena. The richness of the different processes is a crucial asset for the construction of sensitive particle detectors, and it is interesting in its own right. Indeed, it has been a very vigorously pursued field of research of its own ever since the end of the nineteenth century, with the discovery of X rays
(produced when electrons released their kinetic energy as they reached the cathode of an accelerating tube), and then after Rutherford's team bombarded gold foils with alpha particles (helium nuclei) emitted by a radioactive substance.

Of all the phenomena that take place when a particle interacts with matter, multiple scattering is among the simplest to describe, at least in broad terms.  We are talking here about a projectile endowed with mass and electric charge, which travels through a region of space where rapidly varying electric fields reside. 

To be specific, as it is the subject of the studies I am going to  show later, let us take a muon. The muon is a heavier replica of the electron; it can be produced in particle reactions and in particular it rains down the atmosphere (as it is commonly produced as a secondary product of the interactions with oxygen or nitrogen of energetic protons accelerated by astrophysical sources such as exploding stars, black holes, and the like) at a rate of about a particle per square centimeter per minute, so chances are your body is being traversed by about one muon every second, as we speak.

As muons traverse matter, they can do a number of things: kick electrons off atoms, radiate photons, interact with atomic nuclei. You can build devices that are sensitive to any or all of that. But if all you do is to track a muon before and after it traverses a slab of matter, what you will see is that the trajectory has been modified. The muon "scatters" off atoms as it penetrates into their electric field, receiving a small kick of intensity dependent on how close they plunged in the neighborhood of the nucleus. 

The collective effect of millions of such small kicks is a deflection of the particle's trajectory, as well as a displacement orthogonal to the incident direction. Since of the two effects the latter is smaller and less evident, let me concentrate on the angular deflection below.

How can we exploit the deflection of a muon in passing through a slab of material? Well, the deflection per se is not an interesting thing, but it gives us information about the nature of the material that caused it. That is because different materials have different atomic densities and electric field densities. If we can analyze a piece of matter we do not need to study muon trajectories through it, but sometimes we cannot.

In a previous article I discussed how a beam of muons could in principle be exploited to create a precise map of tumours inside patients. In fact this kind of task is today better performed by PET scans or proton tomography, but in a possible future when muon beams will be available and cheap, muons may provide a much less invasive means to achieve the same goal, as muons do not damage the surrounding tissue nearly as much as photons or hadrons do.

But muon tomography is useful in a number of other applications. E.g., to scan containers for forbidden materials: think at a container full of iron going to a foundry, where somebody concealed some spent uranium block that they want to get rid of (uranium storage is damnedly expensive). Or to detect the distribution of material inside a furnace. So let us look into muon scattering a bit more in detail - if we understand it better, we can exploit it.

If we imagine a muon traveling in the z direction, and entering a slab of material orthogonally to its front face, the deflections can be parametrized as angles in the orthogonal x and y directions. These two angles are independent variables, in the sense that while every single scattering interactions connects them to the physics of the scattering, when you observe the collective effect of a number of scatterings they "decouple" and can be studied separately. 

I asked my colleague Jan Kieseler, a CERN scientist who collaborates with me in the MODE collaboration, to produce with an accurate Monte Carlo program (called GEANT4) the simulation of a few samples of muons going through different materials. The purpose is to produce a versatile parametrization of those scattering angles, which may be an important ingredient in a bigger task (optimization of muon tomography with differentiable programming, which I will discuss elsewhere).

Now, let us look at the angle of deflection of muons through different thicknesses of a few materials, to get a hunch of what is going on. First of all, I need to explain that when you study the electromagnetic interaction of particles with matter it is fruitful to measure thicknesses in terms of a quantity called "X0", the "radiation length" of the material. This is a depth of just 5.6 millimeters in lead, which is dense (and has very intense electric fields around its atoms), or several centimeters in lighter materials. In air, one radiation length is 300 meters. 

By studying materials in units of radiation lengths, we decouple from the most relevant scale, and we can concentrate on sub-dominant effects that distinguish the behaviour of the scattering angle: a muon crossing one radiation length of uranium will do something slightly different from a muon crossing one radiation length of aluminum, say, and we want to concentrate on those differences.

Another important parameter in multiple scattering is the muon momentum. A very high-momentum muon will suffer much smaller deflections than a lower momentum one, because a kick transversal to its motion will result in less of a change of its trajectory. As you can see below for the case of a slab of lead, of thickness equal to 0.05X0 (so just 280 microns of it), the deflections (along one of the x,y coordinate) become smaller as the momentum grows: the first row, left to right has muons of momenta of (top row) 0:1,1:2,2:3,3:4  GeV; 4:5,5:8,8:13,13:20 GeV (middle row); and 20:40, 40:80, 80:150, 150:500 GeV (bottom row).




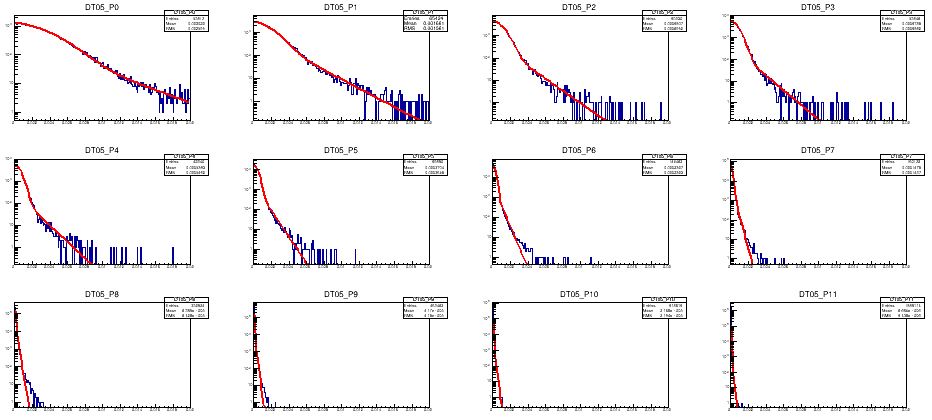
The 12 graphs above should be read as follows: on the horizontal axis is the deflection angle (from 0 to 0.1 radians) resulting from the crossing of 0.05X0 by muons; on the vertical axis is the number of muons that withstood different deflections. The histograms show the distribution of the simulated muons, and the red curves show some rough interpolation of the distributions.

A similar set of graphs, shown below, describe the behaviour of muons when traversing a 0.05X0 slab of calcium, which corresponds to a thickness of 5.08 millimeters. As you can see, the general picture is similar, but there are subtle differences which we need to take into account, and which indeed can be key to exploiting the scattering of muons to detect different materials concealed in unknown volumes.




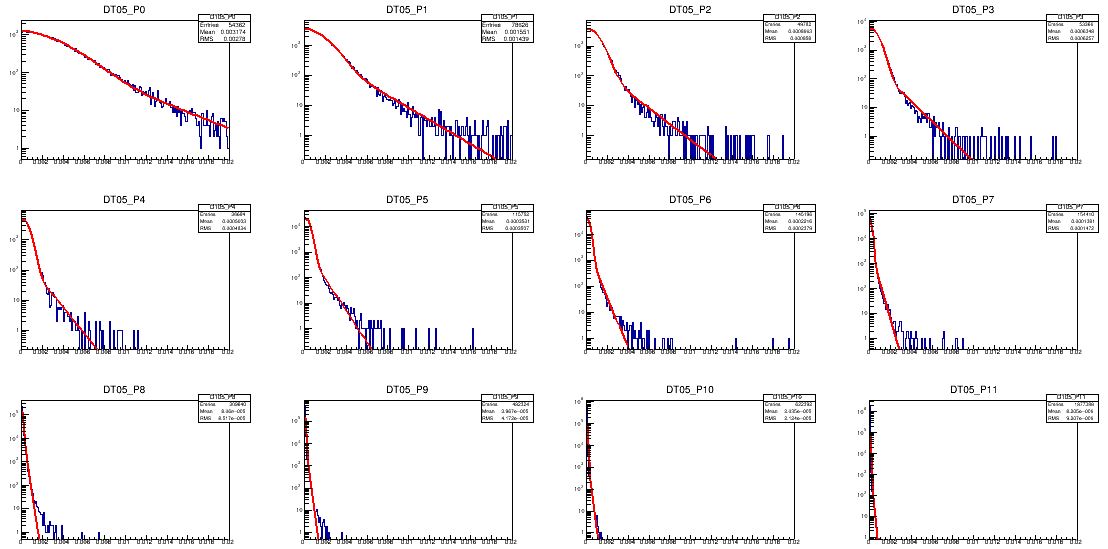
From inspection of the graphs above, one sees that the most probable deflection, regardless of muon momentum, is always azero: this is a common feature of these effects, which correspond to what is called "random walk": if you imagine taking a step to the right or to the left with the same probability, and you repeat the procedure many times, you will find that the most likely position after many (even number of) steps is still at the original point, but the average (unsigned) distance of the final position from the original one gradually spreads out (in proportion to the square root of the number of steps you took). Also, the probability distribution of your location is asymptotically a Gaussian (a mathematical fact due to the central limit theorem).

If you look closely in the figures above, you can see that the distributions of muon deflection angles are not exactly Gaussians. There is, in fact, a small probability that single, close encounters with a nucleus will give the muon a much larger kick - the exponential tails of the distributions are explained by that.

Of course, the study of multiple scattering of muons through materials has been the subject of thorough investigation in the past. However, it is relatively simple to do it on your own, especially if the purpose is the rather special one of finding suitable parametrizations for specific depth of specific materials, in specific momentum ranges, for which the literature may be insufficient. That's why I am spending some time on this, during my vacations in a Greek island (Skopelos)... By the way, this is the closest beach to where I am blogging from, just a 5' walk:






Before you start wondering whether I still have my wits around, wasting time in data analysis when I could dive in that wonderful sea, you should realize that when a physicist turns older than 50 (I am 55), doing real data analysis is a luxury in comparison with the multitude of other less intellectually rewarding tasks (grant proposal writing, bureaucracy, and, to a lesser extent as they do involve intellectual reward, supervision, reviews, refereeing, lecturing). Hence this analysis task had to patiently wait until I left for vacations!