At the smallest distance scales, matter is made of quarks and leptons, which we consider as point-like objects endowed with different properties and interactions. Most of the matter around us is in fact made up of three-quark systems: protons and neutrons, organized in tightly packed nuclei kept together by the strong force; with electrons (which are the lightest charged leptons) orbiting around them thanks to the electromagnetic force attracting them to the protons.
Protons and neutrons are called "baryons" (from a Greek word meaning "heavy, dense"), and we might be happy to end the story there. But the strong force that keeps triplets of quarks together into stable protons and almost-stable neutrons also allows for quark-antiquark structures called "mesons". In a meson, the two constituents orbit around one another, kept together tightly by the exchange of gluons, the carriers of the strong force.
The above two-body picture should be understood to be a simplified description, only valid to provide the immanent properties of these particles (their content), since any particle made of quarks and gluons is in fact a continuously evolving soup of quarks and gluons popping in and out of the vacuum. However, when one of the two quarks is very heavy, the planetary two-body description regains usefulness.
Such is the case of B mesons, which are particles composed of a bottom quark and a lighter antiquark. We can fruitfully think of a b-quark "nucleus" with an orbiting lighter quark jiggling around - and when I say fruitfully I mean that this description allows for predictive calculations of the meson's properties. This is called "heavy quark effective theory" and I will not bother you with its details, but it is important to realize the exceptionality of B mesons - particles which, let me stress it, do not belong to ordinary matter, and can only be produced by very energetic collisions, such as the ones we create at the Large Hadron Collider.
B mesons were first observed in the late seventies, and since then they have been the object of very deep studies. Because of their peculiarities, they constitute an extremely interesting physical system, where we may compare detailed predictions of our theory - the standard model - to what we can measure with precision.
Here we concentrate on one magic trick that the B_s meson (a bottom quark - strange antiquark system) can pull off: their decay into a pair of muons of opposite charge. In physics, anything that is not forbidden by law does take place mandatorily, with some probability that depends on the conditions the system must obey to enable it. Being electrically neutral (the bottom and the antistrange quark have total charge zero) the decay seems like a possible outcome, at least from the point of view of the electromagnetic interaction: we do not create or destroy electric charge. Yet, we are asking two quarks to conjure up their own demise and reapparition in a totally different guise - leptons. How can this happen?
If we had a pair of quarks of the same kind - like a bottom-antibottom meson, for instance - we could imagine that when the two quarks accidentally got very close together they annihilated, producing a virtual photon; the latter would then immediately materialize the large amount of energy it possessed, and this could yield a muon-antimuon pair. But this does not work when we start with a bottom - antistrange pair: the standard model appraises bottom and strange with different properties, which do not give a net sum of zero as would be required for a transition into a dimuon pair.
So in order for a B_s meson to decay to a muon pair, we can ask the electromagnetic and the weak force to work in synergy: the weak force turns one of the quarks into the antiparticle of the other; and then the electromagnetic force may annihilate them. Another possibility is that a "doubly weak" process takes place: a bottom quark turns into a charm quark by emitting a W boson (the charged carrier of the weak force); the charm quark then merges with the antistrange quark of the B_s meson, emitting another W boson; and finally, one W boson decays into muon-neutrino, the neutrino and the other W boson produce another muon, and there we have it - a dimuon pair.
The two processes we described above can be fruitfully pictured via Feynman diagrams, where time flows from left to right and one space dimension is on the other ordinate. Particles are then depicted as lines moving forward, and interactions are three-line vertices. Both of the compound processes described above are then recognized as requiring four separate vertices. Since every vertex is a rather odd occurrence - there is a small probability of each of them - the processes that turn a B_s meson into a dimuon pair are very, very rare. In fact, only about one in a billion B_s meson ends its life that way. Why, then, are we so enthralled by such a rare and irrelevant-for-the-grander-state-of-things process?
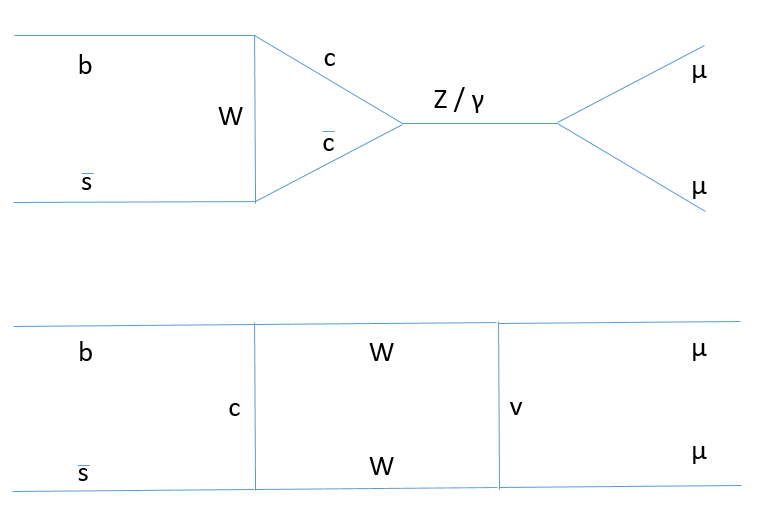
Above: two Feynman diagrams showing processes that allow the decay of B_s mesons into muon pairs by "quantum loops". I apologize for the poor quality of these graphs - I am on vacation, damnit!
One answer I have is that we have no big problem imagining in our head how a particle can decompose into two. Take a piece of goo and pull it apart with your hands - there you have it, a one-into-two process. But now, if you try to imagine similar down-to-earth depictions of a decay that involves a quantum loop as the two shown above, you instantly are at a loss of examples. What you need to imagine is that the goo divides in two, and then the two pieces again split, but one part in each piece magically "reconnects" to the other, disappearing into the void. Or something similar. In all cases, it is heavily counter-intuitive. Magic, if you ask me.
But from a scientific standpoint there is a more concrete answer. Exactly because the studied B_s decay is so rare, it may be a discovery ground for new forces of nature that come at play! For consider: if our theory has, say, a 1% relative uncertainty in the prediction of the probability of different decays, and if we study a decay that takes place 50% of the times, we are going to be comparing a measured rate of 50% with a predicted rate of something like 50+-0.5% (a 1% relative uncertainty, as mentioned). If there is some new physics process that slightly increases the rate, say by 0.1%, then we cannot be sensitive to it, as even with a perfect measurement the rate would amount to 50.1%, which still agrees with our prediction.
On the other hand, take a predicted rate of one billionth. If your prediction is "one billionth plus or minus a hundredth of that", and you measure a rate that is two billionths, this is a discovery of some new interaction that _doubles_ the observed rate - a very significant departure from theory. So you are now sensitive to an extremely weak new physics phenomenon, which only changes the rate by one billionth!
The trick is that the uncertainties in theory predictions (which are based on complex calculations employing the standard model theory of particle interactions) are usually _fractions_ of the predictions. So they are relative uncertainties, and they shrink as the predictions decrease. We could not play this game of looking for rare processes where new weak phenomena stick up as sore thumbs if our theory were subjected to additive uncertainties - that is, absolute ones.
To understand better the above crucial point, consider measuring the amount of water in your bathtub by picking it up with a 0.1 liter graduated cup. Unless you miscount the number of cups you take out, your measurement will be affected by an uncertainty which is of the same scale of the error in each cup's volume - a fraction of it, so maybe of a few cubic centimeters. You will come up with a very small uncertainty in the end. However, if while you take cups out the water can slowly flow out, too, and you can only estimate that outflow during the measurement with a precision of 10 liters, your final measurement contains that additive uncertainty of ten liters, which is not reducible - and it is not therefore very sensitive!
Leaving alone the above lousy example, the B_s decay into muon pairs has other reasons for being a spectacular process. First of all, the two muons are very easy to measure in a detector like CMS, which recently produced the most precise measurement of the B_s to muon pair decay rate. So experimentally we have access to a precise estimate. The other reason to be doing this with as much care as we can is that if there exist heavy new particles that the LHC has not discovered yet, they might contribute to the decay rate of B_s mesons, by modifying those quantum loops we described above. For example, a new particle X could take the place of one of the two W bosons in the second diagram. Even if X had a very large mass the contribution would be measurable!
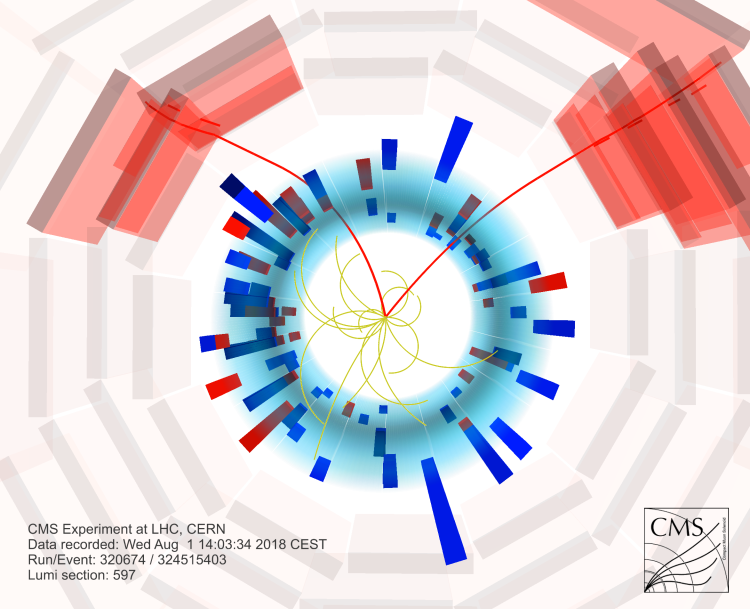
Above, an event display showing two muons from the B_s decay as reconstructed by CMS
The large amount of data collected by CMS in Run 2, which has now been analyzed for this study, allows us to see the B_s mass peak with great precision. This is done by taking the two muons, estimating their momenta (which can be done by sizing up the curvature their tracks withstand in the CMS magnetic field) and computing their "invariant mass", that is the mass that a particle disintegrating into them would have, in order to give the two muons the momenta we experimentally measure.

Above, the CMS data (black points) are compared with a fit (blue line) that includes the B_s decay signal (red) and a contribution from the decay of the "brother" B_d meson (which is made up by a bottom and anti-down quark pair).
As you see in the figure, the peak is extremely well defined, and it provides for a very precise measurement of the rate of the B_s decay. This is found to be 3.8+-0.4 billionths - a 10% measurement, which still constrains new physics contributions to the B_s decay rate to be less than a billionth or so!
Once the rates of B_s and B_d decays to muon pairs are sized up by fitting the data shown above (as shown, the B_d meson is also a possible candidate for the apparition of the muon pair, but it has a mass slightly smaller and the signal is not as prominent for now; its measurement is still affected by large uncertainties), one can compare the measurements to predictions of the standard model calculation. This is shown in the graph below, where you can see that theory and experiment are in great agreement! This indicates that any contributions from new physics processes must really be tiny, if they at all exist.
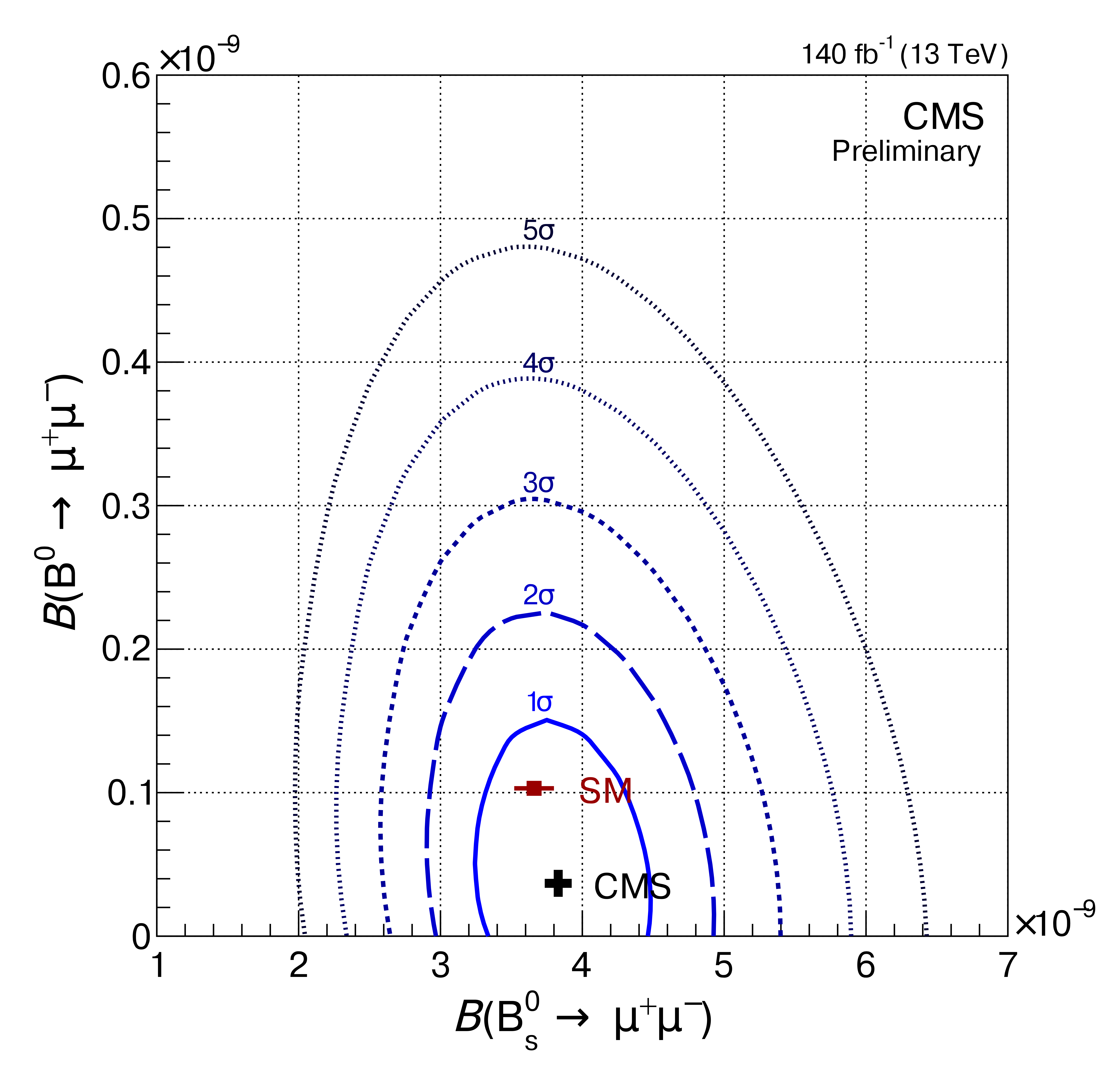
Above, the measurement of the decay rates of B_s (horizontal axis) and B_d mesons (vertical axis) are shown as ellipses centered on the black cross (best estimate). The SM theoretical calculation (in red) is within the "one-sigma" ellipse, so in great agreement with the estimate.
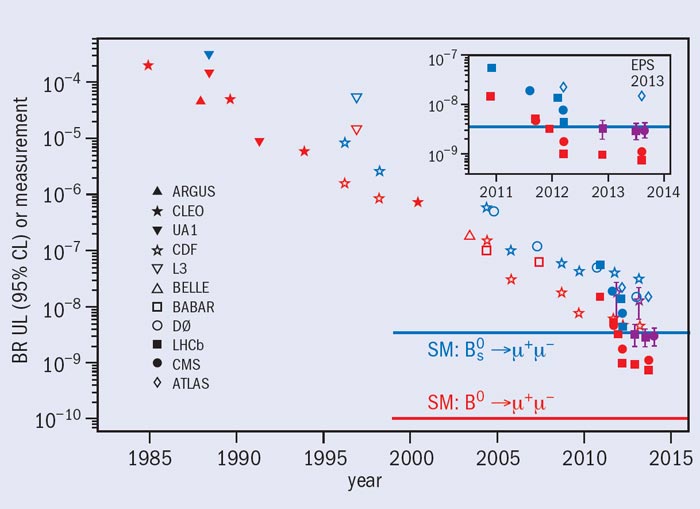
Now, what feels truly awesome to me when I look at these results is that I have been around doing research in particle physics for thirty years now, and I have been able to follow the search for this rare process when the experimental sensitivity was way too small to allow for a measurement. Still, the experiments I was part of (CDF, and now CMS) have consistently continued to improve their reach by collecting more data and improving the precision of measurements and removal of backgrounds, until the peak in the mass distribution appeared - first as a controversial blip, then as a peak, and now as a towerlike signal.
This coherent multi-decade effort, reaching today's precision, almost brings me to tears! The picture below shows the "upper limit" in the decay rate as a function of time, which decreased by orders of magnitude over the years, until the signal was identified in 2012 by CMS and LHCb.
---
Tommaso Dorigo (see his personal web page here) is an experimental particle physicist who works for the INFN and the University of Padova, and collaborates with the CMS experiment at the CERN LHC. He coordinates the MODE Collaboration, a group of physicists and computer scientists from eight institutions in Europe and the US who aim to enable end-to-end optimization of detector design with differentiable programming. Dorigo is an editor of the journals Reviews in Physics and Physics Open. In 2016 Dorigo published the book "Anomaly! Collider Physics and the Quest for New Phenomena at Fermilab", an insider view of the sociology of big particle physics experiments. You can get a copy of the book on Amazon, or contact him to get a free pdf copy if you have limited financial means.




Comments