My talk will be titled "Extraordinary Claims: the 0.000029% Solution", making reference to the 5-sigma "discovery threshold" that has become a well-known standard for reporting the observation of new effects or particles in high-energy physics and astrophysics.
In the talk I will discuss how the criterion slowly consolidated in experimental physics practice, and then discuss its shortcomings and the need of good judgement rather than its blind application. To give you an example, a claim to have discovered that neutrinos travel faster than light is too groundbreaking for even a six-standard-deviation effect to be enough evidence in favor of it.
But statistical significance, expressed in number of sigma, is nothing but a shortcut for reporting a p-value, i.e. the probability of having observed data at least as discrepant to an assumed model (which does not include the effect experimenters are trying to evidence), in a more human-readable way. It is just a mathematical map translating very small numbers to manageable ones, no more and no less than "micrometers" and "nanometers" are shortcuts for 0.000001m, 0.000000001m, or TeraBytes being a good shorthand for 1000000000000 bytes or so.
Some of my colleagues are sometimes distracted by the physics and forget elementary mathematics. So, as I reported elsewhere, sometimes they will incorrectly forget that sigmas are a way to report p-values, and they will directly make a translation from a measurement to a number of sigma.
For instance, if a physical quantity which according to a theory H0 is null and according to another H1 is positive is reported to be measured as 0.110+-0.0027, a unwitty physicist could say "the H0 hypothesis is excluded at 40 sigma significance", as 110/2.7 is indeed 40. This is ridiculous, as it would imply that the probability distribution for the measured uncertainty, whose "one-sigma" is 0.0027, is known to be exactly Gaussian down to very, very, very small tails. It unfortunately was exactly what a otherwise distinguished astrophysicist claimed at a recent conference I attended in Rome ("What Next") last April.
To what p-value does 40 sigma correspond ? Now this is a question less easy to answer than you'd think, as p is so small that most computer evaluations of the integral of the Gaussian distribution in its long tails break down. For instance, the "ErfInverse(x)" function which reports the correct value, if evaluated with the standard "root" program breaks down if x>7.5 - it does not bother to report numbers below 10^-10 or so.
There are however useful approximations of the integral of the Gaussian on the market, and today I came across a very simple and very effective one. It departs by less than 10% from the true value, and can be calculated much more quickly and effectively for significances much higher than 7.5. The formula was reported in 2007 by Karagiannidis and Lioumpas ("An improved approximation for the Gaussian Q-function", Communication Letters, IEEE, 11(8) (2007) p.644), and is as simple as follows (with pi=3.1415926):
Q(x) = [1-exp(-1.4x)] * exp(-0.5*x^2) / [1.135*sqrt(2*pi)*x].
The function is plotted below, for significance levels from 0 to 30 on the x axis.
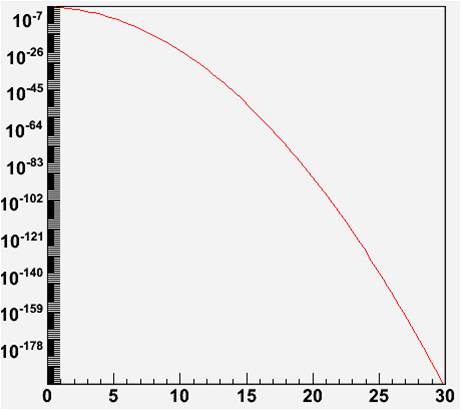
With the approximation of Karagiannidis and Lioumpas we get to know that 40 sigma correspond to a probability smaller than one in 10^320. Do you see what I mean ? If I said that the astrophysicist was basically implying that the measurement had a rather good hunch of not having underestimated some systematic uncertainty, I would be making one of the steepest understatements in the history of science!
I believe that there are very, very few cases when one can safely quote significance levels above 7-8 standard deviations or so; and I also believe that it is rather silly to do that. When very large significances are needed to convince a scientist about the true nature of an observed effect, the scientist would have better take a step back and ponder on the fact that what is really required is not a small number, but coincident, independent proof. The repeatability of experiments, and the multiple ways to measure physical quantities, are the real strength on which to base one's beliefs.




Comments