The CMS Collaboration at the LHC collider has recently measured a non-negligible rate for the fraction of Higgs boson decays into muon-tau pairs, as I reported in this article last summer. The observation is not statistically significant enough to cause an earthquake in the world of high-energy physics, and sceptics like myself just raised a gram of eyebrows at the announcement - oh yeah, just another 2-sigma effect. However, the matter becomes more interesting if there is a theoretical model which allows for the observed effect, AND if the model is not entirely crazy.
The latter seems to be the case for the model put forth by A. Crivellin, G. D'Ambrosio and J. Heeck a few days ago. In their preprint they not only point out how the large branching fraction of a Higgs boson into muon-tau pairs can be accounted for by a not-too-outlandish model; they also show how the CMS observation is "consistent" with two other deviations from the standard model, obtained by LHCb in the measurement of branching fractions of B mesons into K*μμ final state and in the ratio R between the rate of decays B->K*μμ over B->K*ee final states. So, let us look into this a bit more.

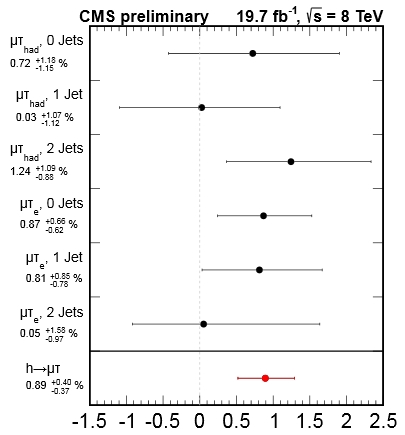Of the 2.4σ H->μτ signal [see picture on the left for the various determinations in different final states, and their combination (red point on the bottom) which is away from the dashed line at zero -the SM prediction] I have extensively discussed in this blog earlier, so let me not do that here. I also discussed extensively the K*μμ anomaly in a post 1.5 years ago. The most recent anomaly, a 2.6σ effect (R. Aaij et al., Phys.Rev.Lett. 113,
151601 (2014), 1406.6482), is in the ratio of branching fractions mentioned above. This is measured experimentally by LHCb at R=0.745+0.090-0.074+-0.036, while the SM predicts it to be essentially unity (1.0003+-0.0001). 

It was pointed out in other papers how the R and the K*μμ anomaly may have the same non-SM origin. 
The news is that the same origin could account for the anomalous Higgs decay of which CMS has a faint evidence. This entails invoking two-Higgs doublet models (2DHM), where instead of a single Higgs boson there are five physical states. 2DHMs are familiar to SUSY seekers, as all minimal SUSY theories require the same Higgs sector. However, 2DHM do not necessarily involve SUSY - they are more general. The added piece to explain the H->µt decays is a violation of symmetry between these two leptons. Authors note that such a violation is needed also to explain atmospheric neutrino mixing. 
Further connections with tau lepton decay phenomenology are a bit harder to explain here, but find proper discussion in the article. However, they are very important, as e.g. the decay of tau leptons to three muons, mediated by a Z' boson, should occur in this model. As the branching fraction of that decay depends on the inverse square of the tan(beta) parameter of the 2DHM, one can connect a lower limit on the decay to the allowed region of tan(beta) of the model attempting to explain the quoted anomalies of CMS and LHCb. This makes the model interesting, as branching fractions of the order of one billionth will be probed in the future, allowing to test the model predictions.

I think I will stop here for now, as the details of this study are too technical for this blog (and I fear I would make wild misrepresentations if I tried to take my imperfect understanding of the matter and work out improbable simplifications). What I can say is that the H->mt effect will be put under the magnifying lens with the data that the LHC is going to start producing at 13 TeV in a few months... Just one more reason to be excited by 2015!