We speak of a fine structure constant (alpha) to address one of the most important parameters of electromagnetism; and we call "strong coupling constant" the coupling strength parameter alpha_s of QCD. But these are not constants at all! In fact, they are parameters that show a quite distinct dependence on the energy of subatomic processes.
The fine structure "constant" alpha exhibits a mild variation with energy, and the effect does not have as extreme implications on the phenomenology of quantum processes as does the energy dependence of the strong coupling "constant" alpha_s. The latter, in fact, varies quite significantly with energy, as it is of order unity at very low energy, and is smaller than 0.1 at the highest energies we nowadays probe at the LHC.
The fact that at low energy alpha_s is not "small" prevents us from being able to calculate precise predictions of low-energy QCD, since it dictates the impossibility of performing perturbative series expansions in powers of alpha_s. Let me explain what that is. Imagine a simple QCD scattering process, whereby two quarks, say, scatter off one another by exchanging one gluon. This "tree level" process can be described by a Feynman diagram like the one shown on the right, where time is understood to be flowing from left to right, and the vertical axis describes the space coordinate; at each vertex (where three lines join) the interaction is proportional to the coupling constant alpha_s, so if you had to compute the rate of the scattering process you would end up with a number proportional to the square of alpha_s. However, the result would be wrong, as you have only considered one among an infinite number of possibilities for the process to take place.
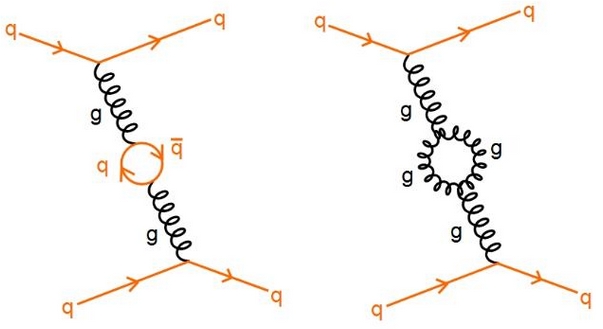In fact, at higher order in the strong coupling constant, the diagram may occur through a number of other more complicated processes (two of them are shown on the right, but there are several others - I just grabbed the first picture I could find from a web search, as it is late and I need to go to sleep). In all of these higher-order diagrams there are four three-particle vertices, and so each of them contributes to the probability of the quark-quark scattering with a term proportional to the fourth power of alpha_s. (for simplicity here I am ignoring other diagrams where there is one more outgoing "leg" -those diagrams have three or more vertices).Now, if alpha_s is a small number, the sum of all the four-vertices diagrams is a small correction to the leading order result: our higher-order correction does not change the main result by much. But if alpha_s is comparable with 1, we are in trouble: we cannot stop the calculation at a fixed order of powers of alpha_s, as what we are neglecting are contributions that produce large changes in the result.
The above problem prevents us from "solving" quantum chromodynamics -e.g. by understanding quantitatively how bound states behave, and predict the mass of the pion, the proton, and the other hadrons. The problem is common to all QCD processes where the energy scale is small. Indeed the large value of alpha_s at small energy, together with the non-Abelian nature of the underlying symmetry group SU(3), is at the origin of all the remarkable properties of quantum chromodynamics. Maybe I will avoid discussing those issues today though, as it really seems a bit too much for this post.
Instead, let us look at a new QCD result by CMS, where the strong coupling constant has been measured at very high energy using events with three jets in the final state collected in data from the 2012 run of the LHC at 8 TeV. Three-jet events allow one to "size up" alpha_s as a function of energy because one looks at a kinematic observable which is correlated with the energy at which the strong interaction takes place: the invariant mass of the three jets. The relative probability of high- and low-mass events then can tell us how strong is alpha_s as a function of energy.
The graph below shows a host of different determinations of alpha_s as a function of Q (the energy transfer of the process). The new CMS measurements are the black points, and the fit to these data is the red line with yellow band in the graph; it is quite precise. Despite not being the most precise way to determine the strong coupling constant, this measurement is quite valuable as it demonstrates that QCD behaves as predicted even in very high-energy phenomena: there is nothing funny happening in the TeV energy range.
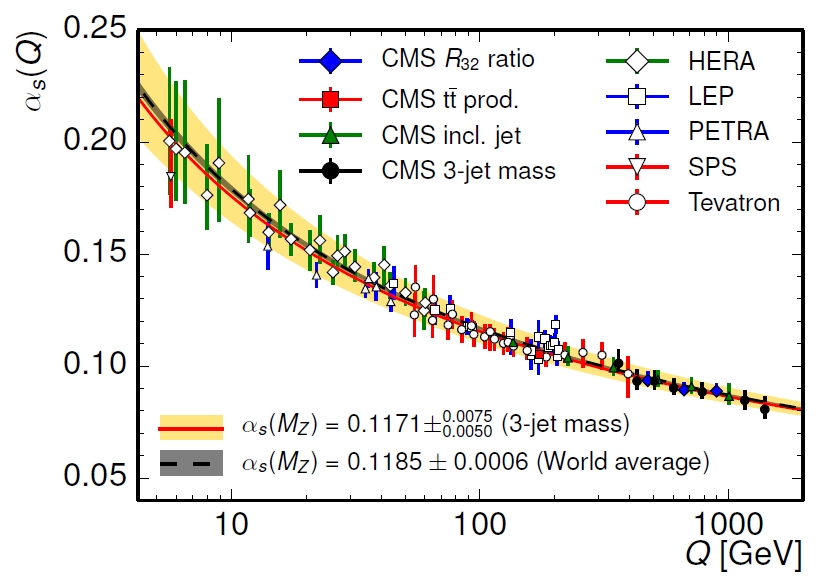
Numerically, the result is reported by "evolving" alpha_s down to the energy reference point corresponding to the mass of the Z boson. In the graph you can see that the result is consistent with the world average.
For more information on this result, please see the arxiv paper here.
Comments