Fresh results from the OPERA collaboration once more confirm the faster than light neutrinos indicated by MINOS. The new findings, available here, also further strengthen a particular scenario: The neutrinos do not travel with superluminal velocity all the way. They only ‘jump’ a small initial distance shorter than 20 meters, after which they settle back and travel as usual with speeds below that of the speed of light. This initial jump would occur at speeds that are more than ten times the speed of light, perhaps even millions of times the speed of light.

The new results make it worthwhile to explain the Ultra Superluminal Small Initial Jump (USSIJ) clearly again, firstly taking into account the new 25 nanosecond “jitter” that affects the new data, but also in order to remove widespread misconceptions. One of the most misleading misconceptions is that the “jump” is a “shortcut” through higher dimensions, perhaps involving SciFi wormholes. Nothing of this sort: It is very much the opposite of a shortcut, in fact, it is a detour (!) in case extra dimensions are involved.

In the following, let us shortly dispel the two worst misconceptions, then introduce the new data, and then argue clearly how they point toward the USSIJ “jump” scenario.

No Extra Dimensions Necessary, No Wormholes!

1) The jump scenario is not dependent on being necessarily a detour through higher dimensions.

2) Even if it is visualized via models with more than three space dimensions, it is not to be confused with nonsense about traveling through wormholes!

Let us first dispose of the second misconception, since the first was discussed at length in previous posts: The so often mentioned “well some say faster then light neutrinos are due to shortcuts through higher dimensions” is very misleading. A shortcut implies some sort of wormhole. Wormholes are odd solutions of the mathematics of general relativity. They are neither supposed to be occurring in our stretched-flat universe, nor are they even expected to be physical in any universe. Classical and quantum considerations both disfavor them. Apart from this shaky basis, they are a completely nonsensical idea if we try to explain the OPERA neutrinos: 

Why would there be a wormhole leading somewhere from CERN to Gran Sasso? The neutrinos create those wormholes? And then they travel through them? That would take so long that they come late, not early. There would have to be preexisting shortcuts, but why right here at CERN? So, they would have to be everywhere and all the time. But wormholes connect almost arbitrarily different space-time events and have arbitrary velocities, too. Why would they stay around earth traveling along with it? Why would neutrinos enter exactly those worm holes that happen to not only go toward Gran Sasso, but also at a very specific time in Gran Sasso? Once and for all: Higher dimensional models in connection with the faster than light neutrinos have nothing whatsoever to do with wormholes!

New OPERA Results Update previous OPERA Results:

The following graph shows the arrival times of the 20 neutrinos that OPERA detected recently over a few weeks; they are plotted relative to the arrival time expected from light, so what we actually see is the time that the neutrinos arrived earlier than light would have:

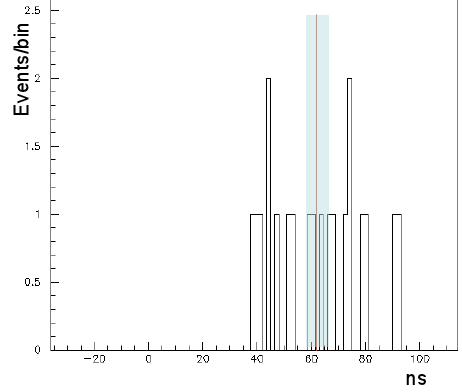
20 neutrinos is very little, but it anyway is just to confirm the previous OPERA results, which are based on 15233 neutrino interactions collected over three years. The arrival times are on average 60 nanoseconds (ns) earlier than that of light. However, there is a "jitter": The individual neutrinos seem to arrive up to 25 ns earlier or later around the average 60 ns of early arrival.

The point of taking the new data is that previously it was unclear whether the early arrival was an artifact brought on by the long duration of CERN’s proton bunches and their perhaps varying focus. The proton bunches have now been made much briefer:

"The modified beam consisted of a single extraction including four bunches about 3 ns long (FWHM) separated by524 ns." Source: Conclusions of recent OPERA preprint.

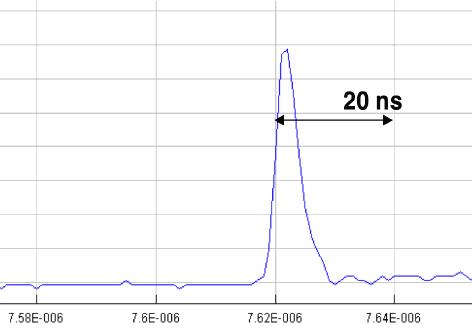
You see that the proton bunch peaks are only three nanoseconds long, which means that OPERA can now measure the early arrival time of each detected neutrino separately rather than infer an average time from the combined measurement.

If you take the spread of the protons into account, the result for the statistical error on the 60 ns early arrival can be inferred. The article goes on:

"With an integrated beam intensity of 4×10¹⁶ protons on target a total of 20 events were retained, leading to a value of δt measured from the average of the distribution of (62.1 ± 3.7)ns, in agreement with the value of (57.8 ± 7.8) ns obtained with the main analysis."

In other words: the statistical error on the 60 ns is smaller than 10 ns. However, there is clearly the "jitter"of 25 ns in the first graph, and it is larger than 10 ns. So, this must be discussed, too.

What do all the Neutrino Data Indicate?

We know already why the neutrinos could go faster and what new experiments this suggests, why it does not imply time travel or violates causality, and why it is somewhat expected for neutrinos. With all this out of the way, let us once more look at the neutrino data and what they actually indicate.

A few years back in Chicago in 2007, MINOS observed evidence for neutrinos moving faster than light (FTL). Under the assumption that the neutrinos travel at a constant velocity [Constant Velocity Assumption (CVA)], the velocity indicated would be just a little faster than the speed of light c, namely at 1.000051 (+/- 0.000029) c. The data from Supernova 1987A in the Large Magellanic Cloud 168 thousand light-years away also allows an interpretation with FTL neutrinos. Under the CVA, they indicate at most a tiny increase over the speed of light. 23 neutrinos were seen over 13 seconds, and they arrived 3 hours earlier than the light. This time delay is mostly due to the fact that during a typeII supernova, neutrinos carry most of the nova’s energy through the outer layers of the star while the visible light comes only out after the shock wave from the stellar core collapse reaches the surface of the star. The recent experiments at OPERA report a velocity of only one part in 100000 above the speed of light, however, again under the CVA!

Looking at all these experiments, the increase over the speed of light is going down along with the increase in total distance D over which the neutrinos have traveled. This is the first indication of that the CVA is wrong. The average velocity is the total travel time t divided by the large total distance D. The CVA assumes that the average velocity equals the superluminal velocity V. Of course, under this assumption, the velocity will become smaller with the increase of the distance D.

So lets take the data seriously and allow for that the superluminal part of the journey is a small “jump” distance x: The particles just travel a short distance x superluminally, after which they travel further with a speed just under the speed of light. The longer they travel afterward, the less the initial short distance x of superluminal propagation at the start is noticeable as an increase of the average velocity.

This assumption will now be further strengthened by considering that the data not only reveal an early average arrival time of about 60 ns, but also a small variation around this average result. I will with some very simple mathematics explain why this small variation also indicates the high velocities V that are much larger than the speed of light c. These very high velocities are expected from all natural scenarios that allow superluminal particles in the first place! The latter was explained in the first article on “millions of times the speed of light”, so I will not bother yet again.

Let me just quip that the many “refutations” of the OPERA results lately, for example that by Cohen and Glashow (http://arxiv.org/abs/1109.6562), not only consider merely the average velocity, but they also assume the CVA. Their argument is basically: Assume the CVA that is actually not indicated by the data and then add that the FTL neutrinos behave completely normal except for that they are obviously FLT and thus not normal at all. Then “derive” from these two faulty assumptions something that is not normal, which is obviously easy to do, and conclude that neutrinos are not FTL because, hey, something not normal showed up. This is obviously not how one can argue.

So now to the meat: The OPERA data are the most reliable. The total distance traveled is D, which happens to be about 730 kilometers. The average velocity is close to the speed of light c = 299792458 m/s. Therefore, the total travel time is t ~ D/c = 2.43 ms. (The “~” will henceforth mean “is roughly equal to”).

The duration of the jump is (x/V) with x the jump distance and V the superluminal speed V > c.

The total travel time t is the sum of the time of the jump plus the time it took to travel the rest of the total distance, namely (D – x)/c (we use c here, because neutrinos are so light that they travel usually with almost c). Hence, t = (x/V) + (D – x)/c.

T = 60 ns is the early arrival time T = (D/c) – t. Put in t from above and get:

T = x [ (1/c) – (1/V) ].

Del T ~ 10 ns is the variation around the average T. (I use bold font Del T here because the greek letters don't go through the editor today). This variation may be due to variations in x and variations in V. The simplest formula for these “errors” is:

Del T ~   Del x   [ (1/c) – (1/V) ] + Del V  (x/V²)

This is almost all we need to consider.

Usual CVA Assumption:

The usual assumption is that the superluminal “jump” x is constant over the whole journey, that means x = D, which in turn implies Del x = 0 and V ~ c. What does that mean for Del T though? Well, obviously only the second term survives:

Del T = Del V (x/V²) = (Del V /V) (D/V) = (Del V /c) t

This implies Del V ~ c Del T / t  ~  3*10⁸m/s  10*10^-9s  / 3*10^-3m/s  ~  1000 m/s.

The total variation on V cannot be bigger than a kilometer per second, which is extremely small compared to the velocity of light. This is unreasonable. If you are close to the speed of light already and bound by the speed of light, then a large increase in energy may in fact only add a single kilometer per second. However, we are already assuming FTL speeds, and all natural scenarios that would allow such make an extremely small variation of only parts in a million hard to imagine: Why should the neutrinos from the very fast mesons decaying bump into exactly such a superluminal velocity? Not impossible, there are always ad hoc assumptions, but lets get back to assuming natural scenarios.

Ultra Superluminal Small Initial Jumps (USSIJ)

The data already hinted at x < D. We should assume such novel physics to be rather contained to the vicinity of the violent origin of the neutrinos*, that is x << D, which implies V >> c. What does that mean for Del T ~ Del x [ (1/c) – (1/V) ] + Del V (x/V²) ?

Because Del V (x/V²) = (Del V /V) (x/V), the variation Del V can all of a sudden be as large as V itself (as would be natural for a “splashing of ether” toy model for example).

If Del V ~ V, the (Del V /V) (x/V) becomes ~ 1 (x/V), and this contribution vanishes below the observed 10 ns error if V is just ten times c. Look: V ~ 10 c implies x ~ 20 m, hence

(x/V) = 20 m / 10 c = 20 m / 30*10⁸m/s ~ 10 ns

Any even higher V than this, the only variation left in Del T is Del x [ (1/c) – (1/V) ] ~ Del x /c. Now comes the 25 ns “jitter”, which is larger than the statistical variation in the results and blamed on the "tagging of the external GPS signal by the OPERA master clock". Even if this were due to variation around x, we would get

Del x ~ c Del T = 3*10⁸ m/s  25*10^-9s = 7.5 m

Now this result, given that at high V >> c the average x is about 18 m, is very reasonable and for example natural in the emergent relativity models discussed previously.

Outlook:

Energy dependence is what should be looked at more carefully next. OPERA's previous results show T to be 54 ns and 68 ns for 14 GeV and 41 GeV neutrinos, respectively, however, those measurements cannot relate to individual neutrinos, so it might be due to more or less neutrinos jumping at all. If the energy just has to get to a certain threshold above which jumps occur, then energy increasing the velocity from 10 c to 10000 c would not change the arrival time. The energy would have to directly change the short initial "jump" distance x in order to show up as energy dependence in the arrival time. If x does not depend much on energy [say it is related to the size of a compactified dimension or the distance between two parallel membranes in a string theoretical higher dimensional bulk space (see universe on a membrane proposals)], less energy may get less neutrinos "jumping", but it would not give energy dependence to the arrival time for those that do "jump".

---------------------------

*A short initial FTL jump allows the possibility that not the neutrinos but the mesons (pions, kaons) that derive from the protons contribute the FTL effects. The muon neutrinos come from the decay of the mesons, but the time of flight is including the whole stretch, including a kilometer of meson shenanigans:

--------------------------------------------

More from Sascha Vongehr Topic by Topic