A multiplet is a simple thing to describe: it is a collection of several identical or nearly identical things. Here, however, a difficulty arises because a "multiplet" is a manifestation of symmetry groups, and symmetry groups are tough objects to discuss. So if in a scientific paper you write "the new hadron might belong to a SU(3) multiplet", you have the additional trouble that you need to avoid discussing group theory to an unwilling listener. What is SU(3) ? Do we actually care?

Thus wrote Tommaso Dorigo in The Language Barrier on 26th May this year.

Well I for one do care.  I have been trying to grasp what this means for years.  So what is the problem?

By now, it is certainly not the Group Theory that vexes me.  However, this is the sort of group theory that neither our Mathematics nor Chemistry departments teaches.  That sort refers to finite groups, as follows:

For our mathematicians:

Galois, in the 1830s, was the first to employ groups to determine the solvability of polynomial equations. Arthur Cayley and Augustin Louis Cauchy pushed these investigations further by creating the theory of permutation group.

       and

In combinatorics, the notion of permutation group and the concept of group action are often used to simplify the counting of a set of objects

While for our chemists:

groups are used to classify crystal structures, regular polyhedra, and the symmetries of molecules. The assigned point groups can then be used to determine physical properties (such as polarity and chirality), spectroscopic properties (particularly useful for Raman spectroscopy and infrared spectroscopy), and to construct molecular orbitals.

For physicists, however:

groups are important because they describe the symmetries which the laws of physics seem to obey. Physicists are very interested in group representations, especially of Lie groups, since these representations often point the way to the "possible" physical theories. Examples of the use of groups in physics include the Standard Model, gauge theory, the Lorentz group, and the Poincaré group.

(Isn’t it nice when Wikipedia has already written half of your article for you?)

No, what I am going to talk about is Lie Groups, named after the Norwegian mathematician Sophus Lie.  These are continuous (or infinite) groups, rather than the finite groups our maths and chemistry friends prefer.  I will not try to illustrate the finite groups, as they quickly become a headache for me, but will move straight on to the Lie groups.

The simplest Lie group to grasp conceptually is the rotation group SO(3).  Imagine a globe standing with the north pole pointing upwards.  Now we’re not simply going to spin the globe, we are going to rotate it, in the mathematical sense.  This means that we take any axis we want (for example one pointing from northern Chile through to China) and then spin it anticlockwise though an angle that we choose.

Here’s where the fun (i.e. the group theory) starts.  Lets us take this globe.  I have marked on it the north pole with a bright circle, a place which I guess is somewhere near Transylvania with a bright star, and right in the middle we see the intersection of the Greenwich meridian and the equator pointing straight at the observer.  (This globe was generated by a Brazilian map projection site, but I have done some subsequent jiggery-pokery with the colours.) 

 

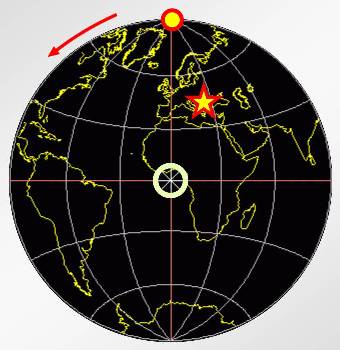
The light green circle at the centre represents the first pole of rotation, and we will rotate it anticlockwise by 45° to get the second globe.  See how the pole and near-Transylvania have moved.

 

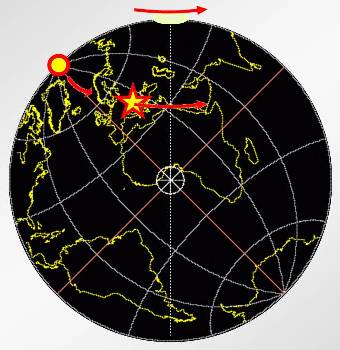
Next we rotate it through an axis passing through the top of the globe (but no longer the geographical north pole) by 45°.  The north pole and near-Transylvania move to the positions shown on the third globe.

 

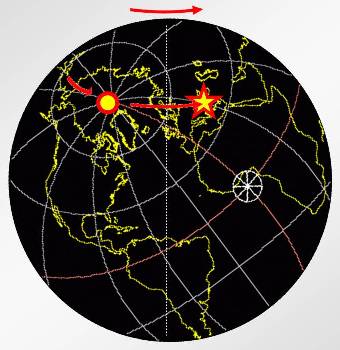
The north pole is now nowhere near where it was to begin with at the top of the globe, but near-Transylvania is back exactly where it started!  So by a theorem found by Euler and developed by Olinde Rodrigues, the first rotation followed by the second rotation add up to a single combined rotation around a pole at near-Transylvania.  This behaviour is general for all pairs of rotations: one followed by another in equivalent to a single rotation somewhere else.

And this is where the group theory comes in.  Each of the two rotations is a separate element of group SO(3), and the combined rotation (the product of the two elements) is a different element of the same group.  “Do nothing at all” is also an element of the group, and is represented by unity (multiply anything by 1 and you get the same thing.)

That, I guess is enough for the present.  We will have to make one or two more stages of our journey to attempt to demystify the “hadronic” statement we began with.

But one question remains.  Is near-Transylvania actually near, or even in Transylvania?  Near, but not quite in.  I calculated the exact pole of the combined rotation using quaternions,  and found that it is a few degrees south, near the border between Serbia and Bulgaria.  Sorry about that, Vlad.