Not many people know, however, that the Higgs boson had been predicted to exist on strictly mathematical grounds--based purely on abstract symmetries usually studied by "pure" mathematicians. As such, the story of the Higgs is even more amazing than you might think--it encompasses a major search that began with the Babylonians and Egyptians and continued to the ancient Greeks, the Arabs, medieval Europe, and on through the nineteenth century to our own time.
The purpose of this note is to make this part of the history of the monumental discovery of the Higgs boson known to a wider audience.
I was first drawn to this story in 2001, not long after my book on pure mathematics, Fermat's Last Theorem, was published and I heard the news that the giant machine, to be called the Large Hadron Collider, was being built under the Swiss-French borderlands near Geneva. Having interviewed a number of Nobel Prize-winning physicists about theoretical physics, I knew that there was a direct relationship between the pure-math concepts I explained in that book and the raison d'etre of the $10-billion-investment being made at CERN: the Large Hadron Collider was being built because of a theoretical hunch based on abstract mathematics derived from the most ancient quest in human history - the quest to solve equations! So let me get to the story.
The quest to solve equations
Both the ancient Babylonians and the ancient Egyptians could solve linear equations, as well as some quadratic equations. We know this from cuneiform tablets found in Mesopotamia (present-day Iraq) dating from the second millennium BC and from Egyptian papyri, such as the famous Ahmes papyrus, 2000-1800 BC. The ancient Greeks, too, could solve linear and quadratic equations, A more general solution method for quadratic equations came with the Arab-Persian mathematician Al-Khowarizmi (c. 780-850) who worked in the Caliph's "House of Wisdom" in Baghdad, and from whose name we get the word algorithm, and from the name of his book, Al Gabr wa al Muqabbala, we get the word algebra.
This book laid out methods for systematically solving the quadratic equation. In the sixteenth century, the Italian mathematicians Cardano, del Ferro, Fior, and Tartaglia developed methods for solving the cubic and quartic equations. But for 300 years afterwards no one knew a general method for solving a quintic--or fifth-order--equation, meaning an equation with leading term being x5--no matter how hard they tried! Then in 1829-1830, a brilliant young French mathematician by the name of Evariste Galois applied himself to this age-old mystery. Galois was just a teenager at the time and smarter than all his teachers. In admission tests to the Ecole Polyechnique in Paris, he was asked to explain logarithms and found the question so offensive that he threw the blackboard eraser at the examiner...needless to say, the genius failed. He became depressed, joined the French Artillery of the National Guard and entered political activity as a Republican, meaning a fighter against Louis Philippe d'Orleans - the King of the French. He was arrested and after being jailed became involved with "an infamous coquette" as he referred to her in a desperate letter to a friend - Stephanie Du Motel - who may have been used by the Royalists to entrap him (we don't know the details) - in any case, he died in a bloody duel outside Paris in 1831, perhaps for Stephanie's "honor," at age 20!
Before he died, he wrote down in letters (and in manuscripts that by then had been rejected by Poisson and Lacroix, famous French mathematicians, as well as not even read by the even more famous French mathematician Cauchy--none of them could or cared or understood it) an entire theory that explained why the fifth-order equation cannot be solved by radicals (meaning in terms of the coefficients of the equation and any fractions or roots of such coefficients, as we do when solving the quadratic using the famous formula). Galois' amazing answer had to do with symmetry.
In this case, the symmetry of the set of solutions to an equation. In developing his incredibly insightful theory--which was only finally understood by mathematicians some years after his tragic death--Galois invented the mathematical concept of a group. Groups are the mathematician's way of explaining and handling symmetry.
Basically, in terms of the application to the original problem: the quintic equation would have solutions with the wrong kind of symmetry, and hence it cannot be solved in radicals (we solve it, today, using numerical methods by computer). But group theory--the young Galois' brainchild--has applications to a huge variety of problems in both pure and applied mathematics: It is successfully applied to solve any kind of problem that has something to do with symmetry.
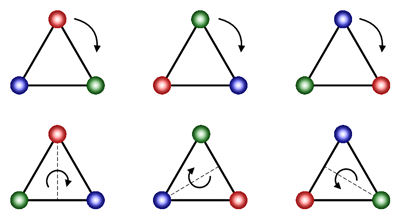
Rotations of a triangle, for example, form a group. These are shown above. The product of two rotations is a rotation, and there is an identity operation: leaving the triangle alone. And operations have inverses: e.g., rotating clockwise once and rotating clockwise twice are inverses since doing both is the same as leaving the triangle unchanged.
About half a century after Galois' work and death, the Norwegian mathematician Sophus Lie (1842-1899; his name is pronounced "lee") sought to extend Galois' work on groups. He knew what Galois' theory of (discrete) groups did for equations, and so he invented (or discovered, as mathematicians would say) a theory of continuous groups, which would do for differential equations what Galois' discrete groups did for usual equations. It turns out that Lie groups are extremely useful in theoretical physics!
The simplest Lie group is called U(1) and it is the continuous group of all possible rotations of a circle: rotations by any angle whatsoever:

It turns out that Maxwell's theory of electromagnetism enjoys a U(1) symmetry: when you rotate the model in an abstract mathematical space, the theory remains unchanged! This fact has been known but not understood well by physicists. Then in the early twentieth century, the German-Jewish mathematician Emmy Noether, who later escaped Nazism only to die in the United States from an abdominal tumor, proved two key theorems in mathematics, called Noether's theorems, which established a powerful link between symmetries captured through Lie groups and the all-important conservation laws in physics. For example: Symmetry through time gives physics the paramount law of the conservation of energy, meaning that energy can only change form (e.g., from mass to sheer energy, as per Einstein's most famous equation) but never be created or destroyed.
Einstein's general theory of relativity has a particular kind of symmetry called "general covariance," which gives the theory its power and validity.
Quantum mechanics is especially amenable to the actions of continuous groups because of the superposition principle. Schrödinger's cat, as everyone knows, is both alive and dead at the same time: Until the box is opened and "the wave is collapsed," the poor cat lives in a superposition, hence a mixture of being dead and alive. The Lie group SU(2), technically called the group of special unitary 2 by 2 matrices, is a group that continually "deforms" one element into another, thus representing such a continuous mixture (continuous because the mixture can be 31% dead and 69% alive, or 23% dead and 77% alive, and so on). The cat can thus be modeled by an SU(2) group, and in fact this idea came from Werner Heisenberg when he tried to model the proton and neutron as a continuous mixture, noting that they were very similar in having almost the same mass.
In 1954, C. N. Yang and Robert Mills wrote a paper that developed the idea further and proposed what we call today Yang-Mills gauge theory (the term "gauge" comes from the mathematician Herman Weyl): a theory of continuous Lie-group symmetries defined independently at all points in space (a property called "local symmetry"). Yang-Mills theory underlies much of the theory of modern particle physics. To jump ahead in the story, the Standard Model of particle physics is modeled by a composite Lie group: SU(3)xSU(2)xU(1). As you may guess, SU(3) is the group that continuously mixes three entities; and here it is used to quantum-mechanically mix the three "colors" of the quarks. SU(2) in this model mixes an up quark with a down quark and the leptons: an electron with an electron-neutrino--the two particles that emanate together in beta decay (hence capturing the action of the weak force; the strong force being modeled by the SU(3))--and the same for the muon and the muon neutrino, and tau with the tau neutrino (and similarly SU(3) also mixes the higher-order quarks of the second and third "generations"). The U(1) part of the composite group can be described (simplistically, here) as representing electromagnetism.
Part of the model, the unification of electromagnetism with the weak nuclear force (responsible for beta decay)--using the composite SU(2)xU(1)--was the work of Steven Weinberg in 1967 (and independently, in different ways, of Abdus Salam and Sheldon Glashow, who shared the 1979 Nobel Prize with Weinberg for the electroweak unification work). in his work, Weinberg used what he called "the Higgs mechanism" to break the original symmetry of the unified electroweak force when it split during the very early universe into electromegnetism and the weak force. When this happened, the Z and W+ and W- bosons that carry the action of the weak force inside a nucleus of matter gained mass.
The "Higgs mechanism," whose action is carried out by the then-hypothesized Higgs boson (now confirmed to exist by CERN) is what gave mass to these three bosons and, by implication, to all massive particles in the universe (save, perhaps, neutrinos, where another process may have been at play). What Peter Higgs, and his colleagues working independently of him and reaching the same results in 1964, Brout, Englert, Kibble, Hagen, and Guralnik, all did was to remove a technical hurdle from the process--that hurdle called the Goldstone-Weinberg-Salam theorem, which stated that massless bosons would appear when a primeval symmetry of the universe was broken. Higgs and the others proved in three independent papers that Yang-Mills gauge symmetry is not affected by the Goldstone-Weinberg-Salam theorem.
In doing so they provided a mechanism by which the continuous Lie-group symmetry of the early universe--a tiny fraction of a second after the Big Bang--can be broken: the composite group SU(2)xU(1), representing a unified electromagnetic-weak force, breaks down into the separate electromagnetic and weak forces, resulting in a new U(1) symmetry (technically, it is not the original U(1) of the composite group) by interaction with the Higgs field. This is what gave us mass during the very early life of the universe--and it all goes back to the pure mathematics of continuous symmetries and the idea of a group developed by Galois and extended by Lie and originally proposed in order to understand why some equations can be solved with pencil and paper while others cannot!
It eventually led to people building a huge, immensely technologically sophisticated, and very expensive particle accelerator--and the greatest discovery in physics history.






Comments