Alpha Centauri is the closest star system to Earth other than our own sun.  So one would think if it had planets, we would know by now, right?  Wrong, apparently.  Astronomers just announced the discovery of an Earth-sized planet in Alpha Centauri, although it's closer to its star than Mercury is to our sun, so unlikely to have life.  However, there may actually be even more planets further out from the star!  So why are we only just now discovering planets in our nearest neighboring solar system, and why don't we know yet if there are more?

Two reasons: planetary mass, and distance from the star.  Unfortunately, the smaller a planet is, and the further it is from its star, the more difficult it is to detect.  This is because of the way we spot planets – by looking for the way they make their stars wobble.  Imagine swinging a heavy bucket around you in circles.  The bucket goes around, but you wobble too, just like planets make the stars they orbit wobble.  As the star wobbles towards us and away from us, there is a doppler shift in the star's light, similar to how a car horn coming at you sounds higher-pitched than a car horn moving away from you.  The size of the doppler shift depends on how fast the star is wobbling.

Ok, some quick math here.  The momentum of a system is conserved, so the star's maximum momentum while wobbling towards us equals the planet's maximum momentum while orbiting away from us, or 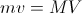(lower case for the planet, upper case for the star).  So the velocity of the star is

 (1)

Ok good, but what's the velocity of the planet, v?  Well, for an orbit to be stable, the gravitational force on the planet 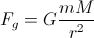  has to equal the centripetal force to keep it in orbit, 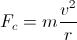.  Set those two equal and solve for v, and you get

(2)

Now, combining equations 1 and 2, we can see how the star's wobble velocity depends on the planet's size and orbit:

(3)

So smaller planets (small m) make a smaller wobble, and planets that are further out (large r) make a smaller wobble.  Since finding this Earth-sized planet that's so super-close to its star already "pushed our technique to the limit", finding Earth-like planets farther out where life (as we know it) could exist will be even tricker.  But techniques keep on pushing, so stay tuned!