A method is needed by which efficient new network routes can rapidly be
calculated to route traffic away from problem paths and nodes. A
possible method is proposed. I propose to call it the Wentrok heuristic.
What Is The Quickest Route From Newtork To Wentrok?
A network is only as efficient as the algorithm used to control its traffic. The most efficient use of resources is achieved when all traffic encounters the least physically possible delay in going from A to B. In real life, this might apply to the internet or to road traffic. In the case of road traffic, a vehicle standing still with its engine running has an instantaneous efficiency of zero distance per unit of fuel. In a dynamic network, failures occur and present themselves as blocked or congested paths (highways) and nodes (junctions and interchanges). In many real cases like this, an improved network efficiency can lead to worthwhile economies.
A network comprises a number of paths over which traffic may pass, together with points of interconnection of the paths. The network graph may describe a computer network or a road network, or any broadly similar real-world routing problem. traditionally, in describing such entities, the terms 'edge' and 'vertex' are used by mathematicians; 'path' and 'node' by many other disciplines.
The generalised problem in such a graph is to find the smallest sum of paths between all possible pairings of nodes. In the generalised model described, an assumption is made that a packet is to be sent between two nodes. This could be a data-packet, or a parcel in a truck.
The Dynamic Network Problem.
In a computer or road network it can be useful to determine the path along which a packet may be sent with least delay. As an example, at peak traffic times it can save delay if a packet is routed away from a choked main highway. Again, a path may be temporarily out of commission: there may be roadworks, or a network server may be down.
The Shortest Path Problem in a Dynamic Network, SPPDN, is a problem of sending a packet from one node to another with the least delay, over a network that has no perfect, permanently fixed structure and which is subject to varying volumes of traffic.
A Proposed Solution.
Based on the notions of six degrees of separation and the magic number six, a heuristic is built in which there is no outside observer or group of observers needed to model a dynamic network. In a sense, the network models itself.
Each node is modelled as a data array in a dynamic network. Adding or removing nodes or paths does not impact on the efficiency of the heuristic. No single node need keep an excessively large list of paths, and the loss of any single path, node or path-list is immediately recoverable by the network overall.
In the diagram, nodes are lettered to show the method. Coloured rings show waves of interrogation. For each node there is a list of nearest neighbours and distances. The heuristic is indifferent to the unit name ascribed to these distances: it may be physical distance for roads, or delay times for electronic signals.
To initiate or refresh a node, as e.g. the one shown in red, the computer interrogates its nearest neighbours and stores the neighbour-labels and route-delays in a look-up table. A refresh is performed as frequently as may be needed to cater for delays due to congestion at peak traffic times.
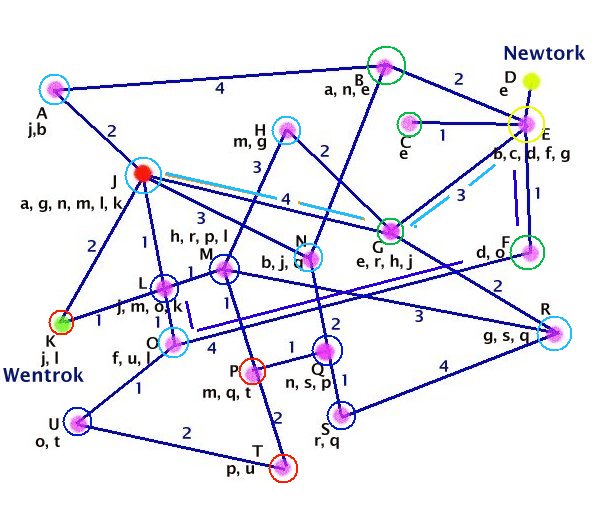
How far is it from Newtork to Wentrok?
Newtork wishes to send a packet to Wentrok by the shortest route. A query is forwarded in the format:
To: Wentrok
From: Newtork.
Node E now sends a 1st wave (green) message to each of b,c,f,g as:
To: Wentrok
From: E, Newtork.
Each of b,c,f,g forwards a 2nd wave (light blue) message. Two examples are given:
To: Wentrok
From: G, E, Newtork.
.....
To: Wentrok
From: F, E, Newtork.
Each node which has no listing for Wentrok adds its own unique i.d. as sender to the front of the sender list and forwards the query to every node in its neighbours list which is not in the senders list. There is a wave-front effect. Ultimately one or more nodes will recognise Wentrok, aka node K, and return the query. The query is returned via the sender list until it arrives back at Newtork. Newtork takes the first instance of a returned list as a de facto validation of a fastest route to Wentrok and sends the packet with an attached routing list.
In the event of a node or route failure during packet transmission, the node which fails to forward the packet initiates a new Wentrok query, and then acts as an initiator of the packet transmission.
In practice, each node may accept a copy of the forwarding list of nodes held by each immediately adjacent node. Thus, node H for example would hold data as m{r,p,l}, g{e,r,j}. The number of 'dimensions' held by any particular node will depend on the computing power available to enact the heuristic.
If each node appends a 'job done' list of nodes already queried, there will be no back-propagation of the interrogation wave. Queries will only be forwarded to nodes not in the senders list and not in the 'job-done' list, with an improvement of efficiency.
Discussion:
If the 6-degrees of connection model is valid, then I suggest that if each computer on a real network such as the internet, being a non-terminal node, has only 6 levels of neighbourhood name-space, then any Newtork-Wentrok shortest route can be determined after a maximum of 6 waves of interrogation.
It is possible that problems involving the exchange of information more generally, not previously viewed as network-oriented problems, may become tractable using this heuristic. The heuristic may thus, perhaps, have applications in linguistics and cell biology.





Comments