A Rotational and Translational motion is standalone natural phenomenon
For this experiment, two identically thin cylinders which are initially static to the observer are taken. These cylinders are attached with internal mechanical springs that induce a repulsive action between them.
Two experiments are to be conducted.
The first experiment.

An action that repels the two cylinders is initiated. This action is induced from their center of mass. Now the cylinders are observed to move in directions opposite to each other. Based on the law of conservation of momentum, the translational velocities of the cylinders are equal. The kinetic energies of the cylinders are deduced using the below derivation:
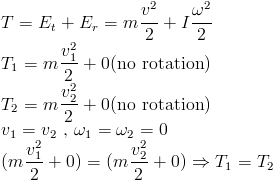
Thus it is inferred that their kinetic energies are identical.
Now, lets compare their translational and angular momentums.
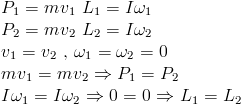
It is inferred that their momentums are identical as well.
This experiment thereby proves that the two cylinders exhibit a symmetric action due to the initial repulsive inducement of their translation movement.

Initiate the same repulsing action as done in experiment 1, but induce the action in different positions. Induce one cylinder from its center mass and the other from its edge. On observing the movement of the cylinders, the following are noticed:
The two cylinders move in opposite directions
The cylinder that is induced from its center mass alone rotates
Assuming their linear velocities are identical according to the law of conservation of momentum, their kinetic energies are determined:
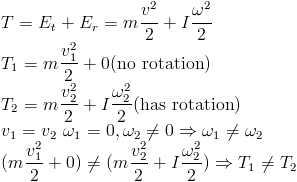
Now, as in the previous experiment, their translational and angular momentum are compared.
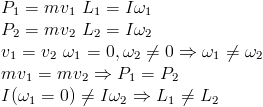
Hence it is deduced that their translational momentums are identical. The values of the angular momentums of the two cylinders are found to deviate and the cylinder initiated from its center mass alone has an angular momentum.
Thus it is assumed that the action is not symmetric, this assumption is made by relating the action to the initial repulsing event. But this presumption fails to follow the law of conservation of angular momentum.
These deviations are however based on faulty assumptions. The linear velocities of these cylinders are not identical.
Newton's First Law: "An object in motion will stay in motion and an object at rest will stay at rest unless acted upon by an external force" or "A body persists in a state of uniform motion or of rest unless acted upon by an external force."
The first experiment conforms to this rule, as there is only one translational motion that is induced. These cylinders have repulsive action aligned from their center of mass and each cylinder of this experiment congruent to single point object. All pieces of these cylinders conducts identical uniform motion.
In the second experiment, one of these cylinders have repulsive action aligned away from his center mass. Each piece of this cylinder conducts it's own motion with it's own cycloidal trajectory. To simplify this cylinder motion to single point object motion require to split this cylinder motion to two simple motions. Rotational and translational motions. In this case, following first Newton's law repulsive event should split to two independent events. Base on this event splitting, the initial force should split to two independent forces. Sum of these forces should be equal to initial net force. An equations with these sub forces will cover rotation and translation motions for this cylinder as single point object.
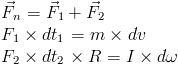
However, to keep situation where one cylinder exhibits translational and rotational motions for one event. These two motions are thus considered as new type of motions. Therefore, this Rotational and Translational motion is standalone natural phenomenon. So it follows, the motion should have it's own momentum and follow its own conservation of momentum. This type of motion can be named as main type of motions. Where rotational and translational motions are parts of this main Rotational and Translational motion.
Assuming the motion has a linear and angular momentum, the total momentum of Rotational and Translational motion is:
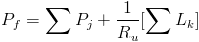
The law of conservation of momentum for the Rotational and Translational motion is:
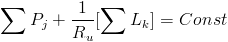
.jpg)
The mass of the rotating body is concentrated on its radius (Ru). An initial force Pf strikes the body which is at a distance h from the center of mass of the body. It is known that the moment of inertia is:
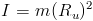
Which implies that:
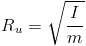
Assuming this momentum is applied to the angular motion:
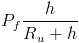
So, the angular momentum is:
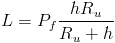
Translation momentum is then equal to:
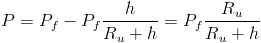
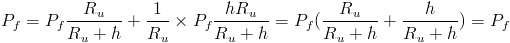
Adding both these equations, the total momentum is determined.
Following the new law of momentum conservation for Rotational and Translational motion, the translational and angular velocities of the cylinders have a different value on experiment 2.
Translation and angular velocities for cylinder 1 equal to:
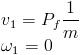
Translation and angular velocities for cylinder 2 equal to:
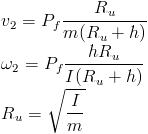
Hence, based on the previous statement, Rotation and Translational motion corresponds to the consolidated translational and rotational motions. It is thus inferred that one of the motion is the result of the other primary complex motion.
The above experiments are simulated.
The experiment 1.
The simulation elicits results that relate to the theory.
Initial results: Before start

Values during experiment:

The experiment 2.

Values during experiment:

Let's simulate same result from experiment using additional torque.
Initial results:Before start

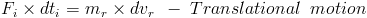
Where, mr - rod's mass, dvr -an interval of translational velocity of rod, Fi - initial pulse force, dti - an interval of time
The red rod on experiment 2 follows these equations:
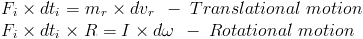
The red rod on experiment with additional torque follows these equations:
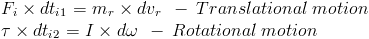
experiment 1 + additional torque = experiment 2
The two rods have same mass and moment of inertia.
However, in experiment 2, the rotating rod exhibits extra torque, which is simulated easily.
Observe experiment 3
The simulator applies extra translation force for rotation rod, which is not the case in real world. A fraction of applied force is spent for rotational motion (torque) then this fraction of force should be detected from the force applied for translational motion. The sum of these rotational and translational fractions of applied force should be equal to applied force for non-rotating rod. (3-rd Newton’s law)The following are the animations recorded for experiment 2:



This animation follows theory of standalone rotation with translation movement.


The Natural Experiment 2.
Equipment:


The following are the snapshots of the experiment dynamics.




Links to experiments movies (avi files)
Experiment 2_1
Experiment 2_2
Experiment 2_3
Experiment 2_1
Experiment 2_2
Experiment 2_3
The experiment results
The experiment results
The translational velocity of non-rotating pencil has value - 2.88 m/s
The translational velocity of rotating pencil has value - 2.17 m/s
The translational velocity of rotating pencil 25% less than translational velocity of non-rotating pencil.
Base on momentum equation (P=m*V) and law of momentum conservation this velocity deference should be in range of mass difference. In case if mass of pencils has difference about 5-10%, the translational velocity should have difference 5-10% also.
However, the translational velocity has difference 25% on this experiment.
The translational velocities of these pencils are not equal.
Conclusion
The experiments using the pencils prove the theory that Rotational and Translational motion is standalone natural phenomenon. This new motion is shown to have its own law of momentum conservation. This theory conforms to the existing classical mechanics laws. This new theory that is framed through this experiment proves existing classical mechanics laws and gives additional natural phenomenon explanations.
email: abelov0927@gmail.com
However, the translational velocity has difference 25% on this experiment.
The translational velocities of these pencils are not equal.
Conclusion
The experiments using the pencils prove the theory that Rotational and Translational motion is standalone natural phenomenon. This new motion is shown to have its own law of momentum conservation. This theory conforms to the existing classical mechanics laws. This new theory that is framed through this experiment proves existing classical mechanics laws and gives additional natural phenomenon explanations.







Comments