You can discuss obesity and weight loss without using math...in the same way you can discuss Astronomy without using math. While there may be a way to present a conjecture in either field using just logic and pure reason, math becomes necessary as the questions tackle more complex and defined aspects of the science. The mathematical regulation of body weight is easy understand and comes directly from a simple energy balance equation with “R” equaling the amount of weight gain or loss, based on calories in, “I”, minus calories expended, “E.”
R = I - E (1)
Of course, a person might feel that describing energy balance this way is so obvious that it doesn't need to be discussed. This would be true, except that the "E" part of the equation is a little bit more complicated:
E = DIT + PA + RMR + NEAT (2)
Because how we expend the calories we take in is broken down to four components: diet induced thermogenesis (DIT) which is the amount of energy we use digesting our food, plus physical activity (PA) like running, working-out, or any other purposeful movement, resting metabolic rate (RMR, which is the brain, heart, liver and kidneys just keeping everything going) and "non-exercise activity thermogenesis," which we call NEAT (including fidgeting and other movements not measurable as PA).
More importantly, all of these things are actually in constant flux. The above equations would really only suffice to describe the energy balance at a given moment in time. But we aren't much interested in math that describes how we are balanced today. We want to know: what is the math that governs weight change? An equation to cover that question, at its absolute simplest, looks something like this:
E = βI + mW + (1 – a){ciWpi – yi(A0+t/365)} + r/1-r(DIT+PA+RMR) + C (3)
Because we need calculus to describe how our bodies change over time. Don't worry, the equation above is just an example, and I don't thoroughly understand it either (point of fact: it's slightly inaccurate, limited by available fonts on my iPad) but it demonstrates that each of the factors involved in energy expenditure, to describe weight loss or gain, would need modifiers that account for how they are regulated during periods of flux. So you include a factor not just for the resting metabolism (RMR) but metabolism as it fluctuates daily with the change in weight and calories. Same idea for NEAT, PA and DIT until you end up with a much more complete and nuanced description, including factors related to time.
The equations above are a small part of a larger construct elaborated by Diana Thomas in a 2009 paper that is part of a growing literature detailing mathematical attempts at modeling the human body’s response to situations of caloric imbalance. The math can be used to explain our population’s weight gain in response to an overabundance of available calories, as well as how an individual body might react to an attempt to eat less or move more. It’s complicated, but probably not something that we can gloss over if we want to truly understand what’s happening with obesity.
Where all this becomes important is when we try to guess what’s going to happen to a patient who decides to cut a certain number of calories per day in an effort to lose weight. There is a general recommendation given to overweight patients by most doctors and dietitians: cut 500 calories per day and in one week, you will have skipped 3500 calories, which is the energy contained in one pound of fat. Using this formula, you should be able to lose a pound a week until you reach ideal body weight. The problem with the formula is that it simply doesn’t work.
Yes, people lose weight when they cut calories, but they seem to need to cut much more than the magic 3500 calorie rule in the long run and they tend to lose much more initially than the pound per week rule would predict. Weight loss is generally faster than expected initially and much slower after a month or so. One reason for the confusion is that the first week or two of weight loss is primarily a decrease in the amount of the food in the gut and changes in water balance. That first ten pounds isn't really pounds of fat.
More important is the fact that, even after we account for water shifting, losing weight grows gradually more difficult. This has to do with a lot of factors, but one that can be explained by mathematics is that the body’s composition changes during a weight loss regimen. We lose more body fat than lean mass. The body fat and the lean mass use different amounts of energy for maintenance, so the equation you use to predict how much a given calorie reduction will change your body weight needs recalibration over time. As we get leaner, weight loss becomes slower and slower on the same calories.
The 3500 rule only works over a period of weeks, when most of the weight change is due to losing adipose (from day 14 to day 74 of a diet, the 3500 calorie rule works fine). As one becomes leaner, the new body composition re-sets the math, making weight loss harder and harder. This is just by the laws of physics, not by emotions or even the hormones and metabolic changes known to occur. The graph of the weight loss over time is a curve, rather than a straight line. It's described by calculus, not algebra or arithmetic.
So, how do sophisticated mathematical models perform when applied to patient populations? Quite well. And getting better all the time. One of the main techniques used to build the models is to take data from well-done weight studies and use those numbers to create equations that will predict weight changes in other populations. The proposed energy balance equations are based on observations of real human weight changes and as more studies are published, the models are re-tested and improved.
As in most scientific endeavors, the researchers at the top of this game are in friendly competition (I actually just assume this, perhaps it's very unfriendly competition, maybe they are armed, I really couldn't say). To read the mathematical modeling articles published over the last several years is to watch the evolution of our ability to predict body weight changes accurately. As the mathematicians get closer, the number of inputs to the models shrinks rather than grows, as they home in on which factors truly matter for weight management.
Right now, the inputs are down to nine in the best model, developed by Kevin Hall and Carson Chow. The model parameters were published in a 2012 paper in The Lancet. An interactive version of their model is available online at the NIDDK website. The nine factors to input into the online tool are:
-Height
-Weight
-Age
-Gender
-Activity level (or metabolic rate, if known)
-Baseline calorie intake
-Percent of carbohydrate in the diet
-Grams of sodium in the diet
-Percent body fat (if known)
Using the first five, the program is able to estimate your current level of calorie intake and probable degree of body fat. You can estimate your percentage carbohydrates and grams of sodium, or the program will assume you are near the U.S. average. Knowing your personal details can improve the predictions and playing with them on the website is one way to see how much each factor matters (spoiler: calories seem to be important).
The online tool is an easy way to get an understanding of the math, without any calculus. Don't be misled by the fact that sodium and percent carbohydrates are inputs into the model. Those are included for the sole purpose of getting the weight loss in the first week (which is based on water, glycogen and salt) correctly estimated. The model does not credit specific dietary choices, other than calories, as determining long term weight. Notice also that most inputs to the model are factors outside of your control.
Weight loss is not linear
In the supplementary materials to the paper describing the Hall/Chow model, Lancet supplies readers with the mathematical discussion that would have bothered most readers if it were included in the article. In it, we are led to the master equation used for energy expenditure. Energy in, the "I" part of the equation, is just the calories we eat. That's never what's difficult to define. What's re-defined in the paper is the current best possible estimate of "E," which is our expenditure of energy. This master equation has too many greek symbols for me to reproduce here, so I will try to convey the meaning of the equation in words:
Energy expenditure can be quantified as the sum of energy needed for resting metabolism added to the amount of energy needed to digest food and move the body. The amount of energy needed to do these things varies by overall body weight, percent body fat, age, and gender. The amount of carbohydrate and salt in the diet can alter weight, particularly in the short term, through changes in glycogen and water balance. Attempts to change the energy balance by altering intake of food will produce variable results depending upon weight and body composition. Since the energy to create fat and lean tissue, the energy needed to maintain these different tissues, as well as the energy they make available to the rest of the body during a reducing regimen, are all different, rate of weight changes will vary depending upon the ratio of fat to lean tissue. As the fat to lean ratio varies in either direction, the predicted weight loss or gain that results from the energy balance equation will change in response. An individual’s ability to partition energy to the different tissues, regulate movement of macronutrients and maintain nutrient balance will account for intra-individual variations in weight loss. The body’s inherent tendency to alter some aspects of energy usage, including metabolic rate and physical activity, will affect the energy expenditure as well.
Maybe I should have just written the equation...
The inputs to the model are not truly new. They come from established science that can’t be argued with, but the mathematical outcomes may be more precise than previous models and the ramifications are surprising.
Weight loss does reach a plateau, but that plateau is not in the typical 6-8 months seen in most diet studies. The calculations demonstrate that a given caloric intervention, since it does not run linearly at a pound or two per week, but curves gradually toward its goal, will yield only about half the weight loss in the first year and 95% in three years. This eventual plateau will represent the new energy balance at the new weight, given a new fat/lean ratio for the individual.
In the example below, I simulated myself, beginning at 145 pounds and reducing my daily diet from 2500 calories (what the program estimates my calories to be at baseline) to 2000 calories per day. Note the different results predicted using the 3500 rule vs. the calculus model.
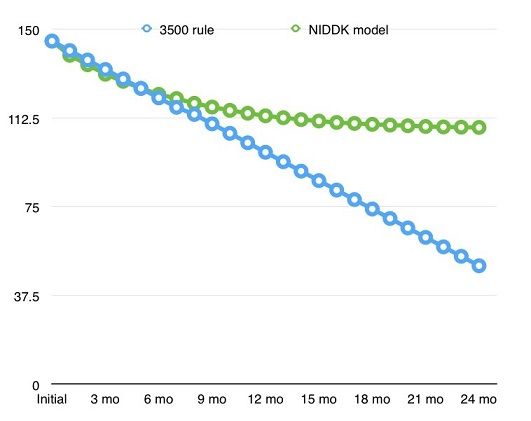
Both equations predict that I will quickly reach an unhealthy weight if I continue to reduce calories for more than a few months, but the NIDDK simulator shows my body adjusting to a near horizontal equilibrium in the second year, whereas the 3500 rule shows me attaining my 3rd grade weight of 50 pounds, or likely dropping dead somewhere along the way...on 2000 calories per day. Surely there is something wrong with that math.
Now let's look at a more reasonable example. Let's look at the results we might see from someone who actually might carry out a long term calorie reduction without danger. Take my average clinic patient, a 305 pound (139 kg) 55 year old female. Baseline calories for an office worker with those characteristics, who doesn't exercise, are 3000 per day. A reduction of 1000 cal/day, to yield a recommendation of a 2000 cal/day target produces the following:

This idealized plot of weight loss over a two year period shows a model simulated weight loss of 96 pounds in two years, assuming strict adherence to a 2000 calorie diet. The 3500 calories rule again produces a highly exaggerated trajectory. In this case, a 192 pound weight loss a resulting in a final weight of 113 pounds. This is a result that I've never seen reported on any diet, or even from surgery. So these two examples give us a sense of how well a math-based model, utilizing calculus, compares to standard dietary recommendations and the 3500 rule. At this point we can dispense with the 3500 calorie rule as too inaccurate. Note that the NIDDK model does show that the patient, on day 730 would still be in an active weight loss mode, not yet in need of reducing calories further to continue weight loss. In my clinic, the few patients who were so consistent as to produce weight loss results like the model predicted, were encouraged at the one year and even the two year mark not to reduce calories more, as the original reduction was still sufficient for continued weight loss. It was counter-intuitive, but proved to be true over time.
However, in real life practice, very few individuals can stay on a dietary intervention long enough to test the models. In large groups, most people fall off the diet because they are hungry, don't like the new rules, get sick, etc. "Life" gets in the way of eating like a robot that can be predicted by math models. For this reason, neither of these above example weight loss trajectories have ever been seen as an average for a group of people trying to lose weight. Published studies of weight loss trials show a plot of the group that invariably looks something like this:

Whether it's a trial of a weight loss medication, or a new diet philosophy, the average weight loss will always follow the above pattern. Initial weight loss abruptly changes direction sometime around 6 months, with gradual weight regain over a year or two. One cannot help but wonder, what happens at six months?
The answer is usually found in the "methods" section of the paper which describes that the participants attended biweekly sessions for six months, or received meal replacement for six months, or medication for six months...with the inevitable consequence that as soon as the intervention is scaled back to see what naturally results, the return to baseline starts fairly immediately.
Generally, to get a study published, you need to follow the participants for one to two years total, but this is much too long to keep the majority of participants engaged, so the weigh-ins are relaxed to 3 month intervals during the follow-up period. The six month turning point is arbitrary, the graph looks the same in three month trials, the upswing just starts sooner. The graph has the same shape for bariatric surgery studies, the trend is just much steeper and swifter on the downside. Regardless of how well the intervention works, the loss will always reverse itself in the long run for the average individual.
Working backward from this highly reproducible graph of weight loss study results to the calorie numbers that would be required to produce it, Drs. Chow and Hall in a 2014 article published in Physiology and Behavior, show that this pattern comes from patients, on average, returning completely to their baseline diet within the first year. It may take many more months for that relative increase in calories to fully work into the body as stored fat and increased weight. The weight gain lags the full resumption of higher calorie consumption by several months. Since weight change happens on a calculus based time curve, the results of a given dietary intervention are much slower than we usually realize. What does this mean for dieting? It means that almost no one has tried anything long enough to know if it works. You would have to continue whatever you are doing for years before deciding whether it was the right diet for you.
Think about how a diet goes: If one adheres to the new food rules perfectly (which is the exception, not the rule) the initial weight loss goes fairly smoothly. If one starts to gradually relax the rules, one is still, on average, calorie negative day to day, so the weight loss continues. After a weekend binge, one might actually weigh five or six pounds more, but that's the weight of the food and salt and water, not actual new fat accumulation. A few days of following the rules and things seem alright on the scale again. As one cheats off and on, for a good deal of time, the body is, again, averaging over a few days, in negative caloric balance and still continues to lose. At this point, the dieting individual has no idea what works or doesn’t work, decides to abandon the whole project and just resume customary eating. Meanwhile, the body doesn’t return to the pre-diet weight for one or two more years, teaching the individual...what? That the amount of food isn’t the problem; it must be something else. What other conclusion could a reasonable person draw after having such strange results from a dietary intervention? Do this a few times throughout your adult life and you might start to doubt the truth of what a calorie is.
References:
Thomas, DM, et. al. A Mathematical Model of Weight Change with Adaptation. Math Biosci Eng. 2009 Oct. 6(4): 873-887.
Hall, KD, et. al. Quantification of the Effect of Energy Imbalance on Bodyweight. Lancet. 2011 Aug 27; 378 (9793):826-37.
Chow, CC; Hall, KD, The Dynamics of Human Body Weight Change. PLOS Computational Biology. Mar 28, 2008.
Chow, CC; Hall, KD, Short and Long Term Energy Intake Patterns and Their Implications for Human Body Weight Regulation. Physiology and Behavior, July 2014.





Comments