The diagram below shows five concentric circles constructed in such a way that the area of each annulus is equal to that of the central circle. Within the first annulus, a square has been constructed such that none of the points on the square lie outside the inner or outer radii of that ring.

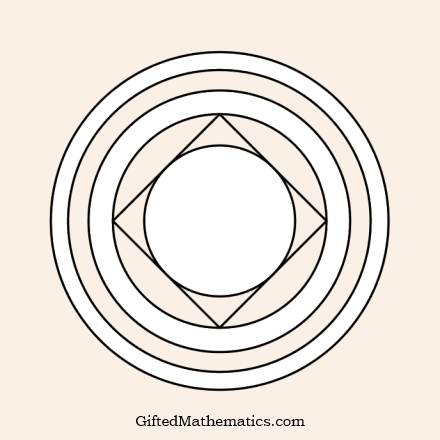
For the first annulus, A(1), with radii r(1) and r(2), n=4 is the minimum value of n such that a regular n-gon lies wholly within or on the boundary of A(1).

Find the smallest value of n, such that a regular n-gon will not fall outside the annulus A(m) bounded by r(m) and r(m+1) for values of m = 2, 3 and 4.

Also, what is the smallest value of n for A(50)?