"You have the choice between two selections: 'even' or 'odd'. The hundred other contestants face the same choice. You all make your choice simultaneously. If the total group of players select an even number of 'evens' and an odd number of 'odds', those who selected 'odd' will receive $3, and those who selected 'even' will receive $4. However, if the result amounts to an odd number of 'evens' and an even number of 'odds', no-one will receive a penny. Now go ahead and make a choice!"
What is your choice?
I suggest you give this half a minute of your thoughts, and note down your choice. We will come back to this game later in this post.
Survival Of The Stupidest
Half a year ago I posted an article on this blog entitled "Survival of the Stupidest". The post got quite a few reactions, and I think it deserves a follow-up. But first a few words about the definition of the term 'stupid'. In the current post I will continue using the same definition of 'stupid' as utilized in my earlier post. This is the definition of stupidity as given by Cipolla in "The Basic Laws of Human Stupidity". So wherever you read 'stupid', keep in mind that I am talking about stupid defined as:
A choice is stupid when it causes losses to others, while deriving no gain and even possibly incurring losses to the person making the choice.The term 'stupid' thus defined allows us to apply the machinery of game theory, and to analyze in detail the impact of strategic choices that don't benefit the individual, nor the group of others. It should be clear that in the following, 'stupid' is not synonymous to qualifications as 'foolish' or 'brainless'. More to the point, in the present context the classification 'stupid' should not be interpreted as an insult. The term is no more than the label of a quadrant of an impact table*:

Cipollo's S4 impact table
Cipolla stresses the importance of the lower-left quadrant in this impact table as follows:
"Our daily life is mostly, made of cases in which we lose money and/or time and/or energy and/or appetite, cheerfulness and good health because of the improbable action of some preposterous creature who has nothing to gain and indeed gains nothing from causing us embarrassment, difficulties or harm. Nobody knows, understands or can possibly explain why that preposterous creature does what he does. In fact there is no explanation - or better there is only one explanation: the person in question is stupid."In the previous post on stupidity I made the case that acting stupidly - consistently harming yourself and others - can equate to being a winner. It all depends on the numbers: stupid choices tend to flourish when others make similar stupid choices. In simple terms: stupid choices become winning choices provided enough players will make stupid choices, and if the effect on the other players is that they harm smart players more than stupid players. Following my earlier post on this subject, I will refer to this phenomenon as the 'survival of the stupidest' (SotS) effect.
I received many reactions to this 'survival of the stupidest' claim. Some react with arguments like: "Forget SotS effects. Just pit a stupid person in a chess game against a grandmaster. The stupid person will derive no benefits from his stupid moves. The grandmaster will tear him apart."
Others pose the question: "How abundant is the SotS effect really? Is it an exotic effect that pops-up in a few carefully constructed example games, or is it much more generic in nature?"
These are very relevant questions. Answering them allows me to elaborate on the SotS effect, to place it in context, and to better specify its relevance.
In terms of the above S4 quadrants, we can split games into two broad categories. The first category are games that force its participants to act like a saint or to act selfish. These are competitive games. Zero sum games like chess have this kill-or-perish character. The second category are games that force its participants to act smart or to act stupid. These are cooperation games.
Selfish Versus Saint
An example of the first category originates when groups go out for a dinner and agree beforehand to split the check equally. When placed in this situation: are you going to order an expensive or an inexpensive dish? The expensive dishes are only marginally better. If you would have to pay for your own meal, you would order a cheap dish, but as the costs will be shared by all, you prefer the more expensive dish. Welcome to the diner's dilemma!
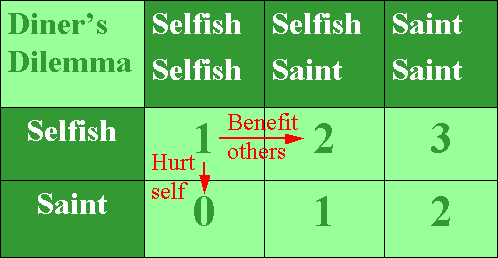
A typical pay-off matrix for a three person Diner's Dilemma is shown above. It lists the net benefit (value of the meal to you minus the costs incurred to you) depending on you choice (left column) and the choices of the other at the table (top row). In the example shown, the fact that the Diner's Dilemma belongs to the Selfish-vs-Saint group of games is made explicit by labeling the choices 'Selfish' (expensive dish) and 'Saint' (inexpensive dish). The situation in which you order the cheap dish, and so does everyone else, leads to the situation in which you pay for and get the cheap dish. This results in a net benefit to you of 2 units (lower right cell in the matrix). The situation in which you order the expensive dish, and so does everyone else, leads to the situation in which you pay for and get the expensive dish. This results into a reduced benefit (1 unit, top left cell) to you. Independent of your choice, your net benefit will increase if more people at your table select the cheap dish, as this will reduce the price that you will have to pay. This is reflected in your benefits increasing in both rows when going from left to right.
You prefer the others to act 'saint-like' by selecting the cheap dish. However, you have yourself a clear incentive to act 'Selfish' and select the more expensive option. This is because, regardless of the choice of the others, you acting selfish will result in an increase of your net benefit of 1 unit. To see this, just compare the lower row of net benefits with the upper row. As all the guests at the table are in the same situation, you are bound to end up in the top left corner situation where everybody pays for and gets the expensive dish. You have found yourself in a multiplayer prisoner's dilemma.
This Diner's Dilemma represents a clear example of a Selfish-vs-Saint game. The rational outcome is given by a situation in which all realize a personal benefit that can not be improved by changing one's choice. Such a situation is referred to in game theory as a Nash equilibrium. The top left corner in the above game matrix represents such a Nash equilibrium. If you would deviate from the strategic choice 'Selfish' and opt for 'Saint', you would hurt yourself as your benefit would reduce from 1 to 0 (downward pointing red arrow). If, however, one of the other players would deviate from the Nash equilibrium, this would lead to an extra benefit to you (right pointing arrow).
Now let's consider how this changes when considering a Smart-vs-Stupid game.
Smart Versus Stupid
An example of such is a game that, as a Dutchman, is close to my heart: the 'Dike Maintenance Dilemma' or 'Dike Dilemma' for short. Imagine a community of people living at the low lands next to the sea. Dikes have been build to keep the water out. However, the dikes run over private properties and the owners of these properties have to work hard and invest in maintaining their part of the dike system. Fortunately for all involved: the landowners have an incentive to do so: if they invest in their dikes and so do all others, they enjoy the benefit of protection against the water, a situation we assign a net value of '5' to. If despite his efforts of maintaining his part of the dike system a landowner does not obtain protection against the water (because at least one other land owner does not put in the same effort), we assign a zero net value to his situation. In that circumstance the landowner who failed to maintain his part of the dike is better off, as he is in the same situation (no protection against the water) but has avoided any investments. This situation we assign value '1' to. What would you do if you were a land owner? Would you incur the expense of maintaining your part of the dike? Would it make a difference if you were in this game with hundreds of landowners or with only a few?
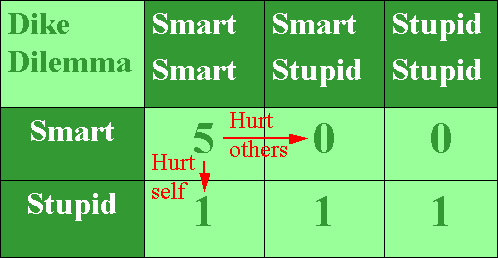
The pay-off matrix for a three person Dike Dilemma is shown above. The fact that the Dike Dilemma belongs to the Smart-vs-Stupid group of games is made explicit by labeling the choices 'Smart' (maintain dike) and 'Stupid' (neglect dike).
The preferred outcome is given by a situation in which all realize the maximum personal net benefit of '5'. This happens when all act smart (top left cell in the pay off matrix). 'All smart' represents a Nash equilibrium, as a single individual deviating from this situation will harm his own benefits (red arrow pointing down). However, in doing so, he will also hurt the others (red arrow pointing to the right). This is the key difference with Selfish-vs-Saint games: in Selfish-vs-Saint games anyone deviating from the expected outcome will hurt himself and help the others, while in Smart-vs-Stupids games anyone deviating from the expected outcome will hurt himself and also hurt the others. Saints help while Stupids harm.
In the above, we focused on the effect of one person acting stupid. However, the Dike Dilemma features a second Nash equilibrium in the form of 'all stupid' (lower right cell).** Although this equilibrium yields a smaller net value and is therefore less preferred than the 'all smart' equilibrium, it is an equilibrium nevertheless and therefore a feasible outcome to the game. If this low-value equilibrium is the outcome, deviating from the strategic choice 'Stupid' and opting for 'Smart', would cause you to hurt yourself as your benefit would reduce from 1 to 0. When you wake up in the morning and, despite your dike maintenance efforts, find your property flooded, you will regret not having acted stupidly. This is the strength of stupidity and key to the SotS effect: stupid choices act as attractor to smart people who fell victim of stupidity.
Where are we now in answering the two challenges?
If You Can't Beat Them, Join Them!
We have already seen the answer to the first challenge of SotS effect being absent in games like chess. This is to be expected, as the game of chess, like any other zero-sum two-player games, is a prime example of a Sefish-vs-Saint game.
The second challenge asked about the abundance of the SotS effect. We can phrase this question more precisely by asking the question: in what games can it be advantageous for a rational participant to select a stupid strategy? The cross-over of rational participants from a smart choice to a stupid choice is the hallmark of the SotS effect. So how abundant is such an effect? We have already seen a clear hint of an answer. And that is that SotS effects occur in virtually every cooperation game. In fact, any cooperation game that features more than one Nash equilibrium is affected by SotS effects, and so are many cooperation games characterized by a single Nash equilibrium. This means that SotS effects can be excluded in no more than a few trivial cooperation games.
Not only the diner's dilemma, but also other well known multiplayer cooperation games such as the volunteer's dilemma and are all affected by SotS effects.
Let's go back to the 'Evan/Odd(s)' game I confronted you with at the start of this post. Did you select 'even'? Good, you understood that with many people involved the outcome to be winning (an even number of evens and an odd number of odds) is basically a 50:50 proposition. So it is best to select 'even' as this guarantees you the better payoff in case of a winning outcome.
Right.
You just have firmly put yourself in the group labeled 'stupid'. You screwed all of your smart co-readers who didn't fail to select 'odd', knowing that if all do so, everyone is a guaranteed winner. Unfortunately, it takes only one stupid person like yourself to render the whole group of smart selectors a bunch of losers.
The winning answer is therefore indeed to make the stupid choice. Park your smartness for a while and select 'even', knowing that you can't trust the hundred fellow participants in the game that each belong to the species Homo Stupidus. They won't all act smart. And if you can't beat them, join them!
One last point:
If you feel uncomfortable about some (or most) of the above, you should check if this discomfort was induced by the terminology rather than by the factual content. To check whether the first is the case, just change everywhere in the above the labels in the S4 matrix. For instance: replace all occurrences of 'Stupid' with 'Streetwise', all occurrences of 'Selfish' with 'Smart', all 'Saints' with 'Stupids', and all 'Smarts' with 'Saints'. Now read again the whole text. Does this make you feel better?
Notes
* In using the terms 'smart' vs 'stupid', and 'saint' vs 'selfish', I purposely deviate from the terminology selected by Cipolla.** Where the Diner's Dilemma can be seen as a multiplayer extension to the Prisoner's Dilemma, the Dike Dilemma represents a multiplayer extension to the game Stag Hunt. Just like Stag Hunt, the Dike Dilemma features two equilibria: a high yield (preferred) equilibrium, and a lower yield low-risk equilibrium.




Comments