Winston Churchill liked his chocolate and he liked it rich and dark. At least that is what Hitler must have been convinced of as he decided to lure the British prime minister not with cigars but with dark chocolate. Churchill barely escaped his death by chocolate and went on to win the Nobel Prize in literature.

Coincidence?

According to New York cardiologist Dr. Franz Messerli: maybe not. Messerli dares to ask the question "How much chocolate does it take to win a Nobel?" and does not shy away from providing us with an answer.

No kidding. We are talking research reported in the most prestigious peer-reviewed medical journal in the world. A journal that amongst all scientific journals in the world ranks number three in terms of impact factor, just behind Nature and Science. Evidently, this is serious stuff we can't brush away as yet-another-fun-correlation-to-make-you-smile. Have a look yourself.

Where to start?

You don't need any degree in medicine to see this article makes more than some occasional errors. Frankly, I wonder how this rubbish could go viral in the popular media (Time, Reuters and Forbes) without anyone pointing out its many flaws? And more importantly: what on earth caused the editors of the New England Journal of Medicine to accept and publish this paper?

I reproduce the plot that forms the core of Messerli's article:



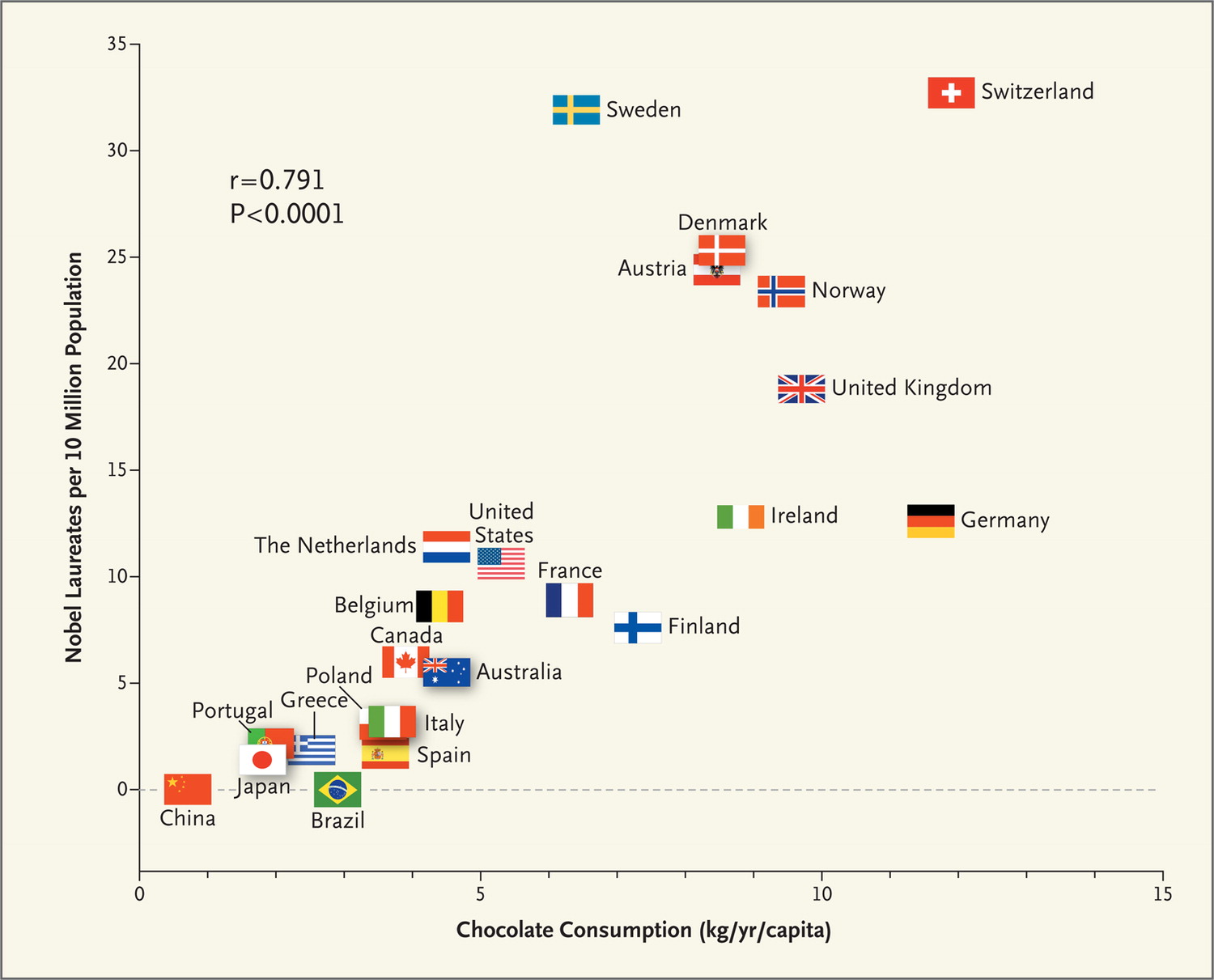
Messerli writes:

"There was a close, significant linear correlation (r=0.791, P<0.0001) between chocolate consumption per capita and the number of Nobel laureates per 10 million persons in a total of 23 countries [..] The only possible outlier in the figure seems to be Sweden."

Say what? Only possible outlier? What about Germany? What about Brazil? Messerli cleverly avoids putting into the figure the trend line he is advocating. I can guarantee you that whatever regression line he would put in, Brazil's chocolate consumption is about an order of magnitude too large compared to its Nobel Prize count. The same applies, albeit to a somewhat lesser degree, to Germany, Spain and China.

But ok, I can forgive Messerli his overly optimistic description of the outlier statistics, would that be his only error. But it isn't. In fact, his conclusions go completely astray due to a loose handling of units. Messerli writes:

"The slope of the regression line allows us to estimate that it would take about 0.4 kg of chocolate per capita per year to increase the number of Nobel laureates in a given country by 1."

This is patent nonsense. Maybe Messerli means to say "it would take about 0.4 kg of chocolate per capita per year to increase the number of Nobel laureates per 10 million inhabitants by 1". But even that would be incorrect. The problem is caused by a sloppy use of units. The point is that the vertical axis in Messerli's plot shows the total historical number of Nobel laureates per 10 million capita. Would someone make the same plot say ten years into the future, all the data as well as the regression line will shift, simply because the total number of Nobel prizes will have increased by then.

This problem can be avoided by properly normalizing the quantity displayed on the vertical axis. In fact, one can argue that Messerli is effectively plotting the number of Nobel laureates per century and per 10 million inhabitants. So the correlation Messerli derives is not "0.4 kg per capita per year per Nobel" but rather "(0.4 kg/year/capita)/(Nobels/century/10 million capita)".

In other words: 400 million kg of chocolate would correlate with one Nobel prize. This goes against Messerli's conclusion that to increase the Nobel count by one "for the United States, that would amount to 125 million kg per year".

Messerli's worst sin, however, is not his sloppy use of units. The most astonishing error stares us in the face when in the article he brushes aside a common cause between chocolate consumption and Nobel prizes:

"it is difficult to identify a plausible common denominator that could possibly drive both chocolate consumption and the number of Nobel laureates over many years. Differences in socioeconomic status from country to country and geographic and climatic factors may play some role, but they fall short of fully explaining the close correlation observed"

and concludes that a causal relationship between the consumption of chocolate and cognitive capabilities is the likely explanation for the observed correlation:

"it seems most likely that in a dose-dependent way, chocolate intake provides the abundant fertile ground needed for the sprouting of Nobel laureates"

That takes the biscuit.

Dear Dr Messerli and dear editors of the New England Journal of Medicine, may I suggest that a country that spends more on chocolate might perhaps also be capable of spending more on education? Just my two cents.