I promised you a toy model to elucidate the information-theoretical entropy that was introduced. You have been waiting patiently, and you get your new toy today. But before we start playing, let's test your patience for a few more minutes, and first expand upon the results obtained in the previous blog post.
Trivializing The Second law
Thermodynamics is about energy and bits contained within a volume. Ok, also such things as pressure and temperature pop up in thermodynamics, but the first is just energy per unit volume, and the second is nothing else than energy per bit. (*) So, energy and bit count it is, and nothing else.
Thermodynamics has a law for both energy and entropy. The first and second laws of thermodynamics. The first law states that energy doesn't change, and the second law states that the bit count doesn't decrease. Energy we are all familiar with. But what's the deal with bit counts? Why can bit counts not decrease? What bits make up these counts? If you have read and understood my last blog post, you know the answer.
The bit count, also referred to as the entropy, measures missing information. To put this slightly more precise: entropy quantifies the detailed information we lack about the system. It is the minimum number of additional bits that you need in order to be able to fill in the hidden information and to describe the energy configuration of the system down to its finest details. The second law of thermodynamics states that this missing information can't decrease. If we are ignorant about the finer and fast details of the system, that ignorance can not disappear due to the system evolving. Ignorance can spread and grow, but it can't disappear. That's all there is to the much celebrated second law. (You are not disappointed, are you?)
How do we quantify the missing information?
Well, that's easy provided you know the total number W of micro-states of the system, which each are compatible with all the information youdo have on the system. (**) To specify the precise state of the system, you need unique labels for each of the states. To get a bit count, you need binary labels, and to minimize the bit count, you want short labels. An obvious choice is the labels 0, 1, 2, .. , W-1 written in binary notation. If in binary notation W-1, one minus the state sum, contains S symbols (0's and 1's), each of the state labels can be transmitted in S bits. That makes S, the bit count of W-1, the number of bits required to specify the system. Presto.
Let's take as an example a simple dynamic system for which we can easily do the state counting: a system of eight coins. (***) We start with all coins showing heads: HHHHHHHH. At discrete time steps we turn a randomly selected coin. That is the whole dynamics. We know that at time zero we can only have one state: HHHHHHHH. At the next time step we have eight possible states that are equally likely: HHHHHHHT, HHHHHHTH, .. , THHHHHHH. After a large number of time steps an equilibrium is reached in which you will need to distinguish 28= 256 equally likely states. At that stage, the number of states does not grow any more.
So what does this mean for the entropy of this eight-coin system? At time zero we have W-1 = 0. In binary that translates into an empty string: an entropy of 0 bits. That is compatible with the fact that we don't lack any information on the system. We know for sure the system is in the precise state HHHHHHHH and there simply is not more to know about the system. At the next time step we have W-1 =7. In binary that reads W-1 = 111bin, a three symbol string and hence an entropy of 3 bits. And finally, after some time the system reaches a state sum value W-1 = 28 - 1 = 11111111bin states. That corresponds to an equilibrium entropy of 8 bits.
So even without invoking the second law, we predict the entropy to increase. First from 0 to 3 bits, and then to higher values until the bit count settles at 8 bits. Again, we see that the second law of thermodynamics is a logical consequence of the fact that we are dealing with complex systems with lots of details on which we have only partial information.
OK, now that we have grokked the second law, it's time to unpack the toys.
Dynamic Dominos
Traditionally, the systems studied by thermodynamics take the shape of gases of interacting particles, melting ice cubes in water, and the like. However, we now know that thermodynamics can deal with a remarkably wider range of systems. We have already seen that coin configurations are amenable to the methods of thermodynamics. This also holds for magnets, stellar clusters, and black holes. As long as you can identify energy content and can indicate missing bits, you are in business.
What about tiling patterns?

Yes, tiling configurations can also be thermodynamic in nature. However, we should not limit our attention to static tilings such as the floor tiling shown above. To obtain a thermodynamic toy model we can learn from and use to sharpen our intuition, dynamic tiling patterns are the way to go. Something like this:

What you see here is a rapid succession of tiling patterns. In this particular case, we are looking at tessellations of a 3x2 rectangular region by 2x1 rectangles. Believe it or not, but physicists do study such toy systems. In statistical physics literature these models are referred to as "domino tilings" or "lattice dimer models". (I guess the latter term can be beneficial in rendering the funding for this type of research less problematic.)
At each moment in time, the 3x2 rectangular region shows one of three possible domino tiling patterns. However, you have to imagine the dominos to change configurations at the speed molecular configurations in water change. Simply put, the random succession of the tiling configurations happens way too fast to follow. Lacking the information that tells us at every moment in time in which exact state the system is, we can still measure the size and geometry of the region. In this case, having established a size of 3x2, we do know for sure that at any moment in time the system is in one out of three possible configurations. With W = 3 accessible states we have: W-1 = 2 = 10bin.This gives an entropy of S = 2 missing bits.
Now a 3x2 region is small and limiting. What happens if we study progressively larger tiling patterns? One might expect the thermodynamics of even the largest domino tilings to be rather boring. After all, these are systems that might be assigned bit counts, but their energy behavior is, out of necessity, rather trivial. In fact, to enforce energy conservation, one can assign nothing more than a fixed energy to each of the dominos that make up the tiling. This causes a complete absence of interparticle potential energies, and therefore an absence of any energy transfer. This also means we can not feed to or extract from the system specific amounts of energy. So we can't thermally push the system through phase transitions like freezing and melting.
All one can do to trigger domino tilings into interesting behaviors, is to change the size and shape of the tiling region. Unfortunately, one can not expect to push tiling systems into entropically dramatically different behaviors, just by changing the shape of the region containing the pattern. This intuition can be made plausible by invoking the "Tetris argument". Following this argument we assume the tiling pattern to be build by playing a game of Tetris. A steady stream of dominos enters from a well-defined direction, and a player tiles thewhole region by judiciously applying right angle rotations to some of the dominos, and, if required, by laterally displacing some of the dominos. All of this to ensure all dominos fall in place without leaving any gaps that can not be filled later.
Suppose we can replay the Tetris game with the same stream of dominos entering. How much information would we need to build the exact same domino pattern as before? We can assume that playing Tetris with shapes as simple as dominos is relatively easy, and that a player hardly needs any lateral displacements of dominos entering. However, that still leaves us with the need to specify one bit of information per domino: rotate the domino or not.
This means that no matter the exact shape of the region, for large sizes we should expect about 1 bit per domino to be required to specify the tiling. So not only is their energy behavior trivial, the entropy of domino tilings can be expected also to be boring with a uniform 1 bit per domino being assigned to the entropy.
Have I convinced you that domino tilings are the dullest thermodynamic systems ever invented? Good! Please read on: you might be in for a surprise!
Counting, Counting, ...
Let's grow the 3x2 tiling region. We do this in two distinct ways that each create successive generations of tiling regions of ever increasing size, each with its own shapes. Counting the tiling patterns for these shapes will allow us to check if the shape of the region has any effect on the thermodynamic behavior of the domino patterns.
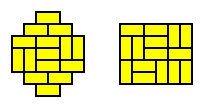
One way to grow larger and larger regions is to create a next generation by gluing squares to all the edges of the previous generation. Starting from the 3x2 region this leads to a succession of regions growing into diamond shapes as shown in the left-hand side of below figure. An alternative way is to grow ever larger rectangles by adding a full row of squares to the top and both sides of each previous generation (right-hand side of below figure).

Let's compare the two regions that can be grown from a 3x2 rectangle. Both these regions contain eight dominos. The diamond region looks like a 5x4 rectangle with the corners removed. It accommodates 13 distinct patterns.

The rectangular region happens to be square (4x4), and contains as many as 36 distinct patterns.

That is a significant difference in number of states for two equally large regions both contain eight dominos.
A total of 36 patterns corresponds to W-1 = 35 = 100011bin, and requires 6 bits to distinguish between the 36 realizations. That is 6/8= 0.75 bit per domino. Somewhat smaller than what the "Tetris argument" made us believe. Let's now look at the regions that accommodates only 13 realizations. This corresponds to W-1 = 12 = 1100bin, and requires 4 bits to distinguish between all 13. That is 4/8 = 0.5 bits per domino, considerably smaller than expected.
Let's grow the regions again once more and see what happens.
We arrive at a 6x5 rectangular region and a region that looks like a pixelized diamond. Both contain 15 dominos. The rectangle accommodates 1,183 tiling patterns, and the tilted square only 63. (***) Now that is a surprising difference. Let's calculate the entropy per domino. Using 1,182 = 10010011110bin and 62 = 111110bin, it follows that the two equally sized areas hold 11 and 6 bits, respectively. That is 11/15 = 0.73 and 6/15= 0.40 bits per domino. In both cases the bit count per domino has dropped further.
One more growth step: we now arrive at patterns containing 24 dominos. Without providing any details, let me give you the bottom line. The rectangular (8x6) region contains 167,089 (!) distinct patterns, the diamond, however, contains no more than 321 distinct patterns. That is noting less than a shocking difference. These figures translate into an entropy of 18 bits, 0.75 bits per domino, for the rectangle, and 9 bits, 0.375 bits per domino, for the diamond.
We see that in contrast to what the "Tetris argument" suggests, the number of patterns does depend dramatically on the exact shape of the region. For the rectangular region we witness a steep growth of patterns with size, leading to a bit/domino ratio that seems to converge to a value of around 0.75. For the tilted square, the number of patterns grow much less steeply, with a bit/domino ratio that continues to drop with growing size of the region.
What is happening here?
What we are witnessing here is a phase transition from a 'molten' domino pattern into a 'frozen' pattern. This phase transition is induced by morphing the shape of the region from rectangular into a diamond. The frozen pattern manifests itself as a "brick wall" configuration that can be made pronounced by giving the dominos that don't fit the brick wall pattern a contrasting color.
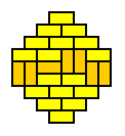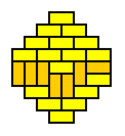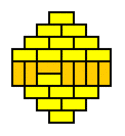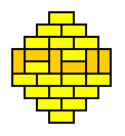
The frozen patterns take shape of extended North Polar and South Polar regions, separated by a molten equatorial band that takes erratic shapes. This completely invalidates the "Tetris argument", which assumed that the player had a lot of freedom in filling the region with dominos. This is certainly not the case for the diamond regions that require the vast majority of the dominos to fit a unique "brick wall" pattern.
Note that the observed phase transition occurs in the absence of any energy potentials between the dominos. The transition is purely entropic in origin.
From Domino Tilings To Black Holes
One last word about the low entropy for domino tilings on diamond regions. This entropy results solely from the molten equatorial band: the only locations where there is some freedom to place and orient the diamonds. This suggest that one should not calculate the entropy/domino ratio, but rather the entropy/girth ratio, where the girth is defined as the number of cells stretching horizontally where the domino is at its widest. Indeed, the first order domino (the 3x2 rectangle) has an entropy of 2 and a girth of 2, resulting in entropy/girth ratio of unity. The next order diamond (accommodating 8 dominos) has entropy 4 and girth 4, again a unity ratio. For larger diamonds, the entropy/girth ratio increases slightly but stays close to unity. For very large diamonds, it approaches a constant value 1/2 log2 (3+2sqrt(2)) = 1.27.
Effectively what happens is that these two-dimensional tiling pattern behaves such that in terms of their entropy they seem to be one-dimensional.
Does this ring a bell? Indeed. What we have here is probably the simplest system displaying holographic entropy behaviors, in which the non-frozen degrees of freedom take the shape of a lower-dimensional geometry. Holographic degrees of freedom. A behavior that domino tilings share with black holes. Counting micro-states is a powerful method in statistical physics, and key to our understanding of a wide variety of macroscopic behaviors.
Notes
(*) To be more precise: pressure measures the change in energy due to changes in the volume, and temperature the change in energy due to changes in the bit count.
(**) in the physics literature such state counts are referred to as"partition functions". These partition functions take central stage in statistical physics. If for a system you know the partition function,you can derive all thermodynamic quantities of interest.
(***) No, I am not going to show pictures of all these configurations. There is just far too many of them. You either check for yourself and count all realizations of ever growing tiling patterns, or you take my word for it and accept the numbers I provide you with. To give you a bit of reassurance that I am not just dreaming up numbers: there is a whole mathematical machinery at work behind the scenes. For instance: it can be proven that the n-th generation of the diamond region has Wn distinct tilings, with Wn being the n-th central Delannoy number. This number satisfies the recurrence relation n Wn = 3(2n-1) Wn-1 - (n-1) Wn-2. Starting with W0 = 1 and W1 = 3, all Wn's follow.




Comments