The Mystery of Entropy (1)
What is entropy and what does entropy have to do with order and disorder? We know what order is. The concepts of order and disorder have been part of our consciousness since long before the notion of entropy was ever invented.What Order Is
Order is having everything in its proper place, behaving in its proper manner. Disorder is the opposite. Order is trains running on time, people getting to where they need to go, and shipments arriving on schedule. Order is troops reporting to their proper posts to perform their proper duties in accordance to their commander's orders. Doing otherwise causes disorder in the ranks. Order is a well tuned machine with all its parts moving in perfect coordination with all other parts. A machine with parts not behaving as they should is a machine that is out of order.Order does not necessarily involve movement. Sometimes "doing the proper thing" means remaining in place, as when items are categorized and stored. Books in a library are in order when each is resting in its proper place, on the proper shelf. Likewise, cans of soup in the grocery store and files in a file cabinet are in order when each is resting in its proper place. In other words, order can be dynamic or static.
Pop Quiz
So what is entropy? Probably the most common answer you hear is that entropy is a kind of measure of disorder. This is misleading. Equating entropy with disorder creates unnecessary confusion in evaluating the entropy of different systems. Consider the following comparisons. Which has more entropy?- stack of cards in perfect order or a stack of cards in random order?
- a Swiss watch with intricate internal workings or a sundial?
- ten jars of water stacked neatly in a pyramid or the equivalent mass of water in the form of 10 blocks of ice flying randomly through space?
- a living, breathing human being or a dried up corpse turning to dust?
- the universe at the moment of the Big Bang or the universe in its present state?
If you think of entropy as disorder, then the answers to these questions may trouble you.
Entropy According to Classical Thermodynamics (2)
Let's take a look at where the idea of entropy actually came from. The concept of entropy originated around the mid 19th century, from the study of heat, temperature, work and energy, known as thermodynamics. This was the era of the steam locomotive. The study of how heat could be most efficiently converted to mechanical work was of prime interest. It was understood that there was a relationship between heat and temperature. Generally speaking, the more heat you applied to an object, the hotter it got. It was also understood that heat and work represented different forms of energy and that under the right circumstances, you could convert one into the other. Furthermore, it was observed that the only time heat would spontaneously flow out of one body was when it was in contact with another, colder, body. That is, heat always flowed from hot to cold. The challenge was to find the most efficient way to harness heat flowing out of a hot reservoir toward a cold reservoir and use it to do mechanical work.One of the difficulties was knowing how much heat energy was stored in the hot reservoir. What was the maximum heat that you could theoretically withdraw from the reservoir? You couldn't measure the heat content directly. What you could measure was the reservoir's temperature. If you knew the relationship between the temperature and the heat content for that reservoir, you could use the temperature to calculate the heat content. Furthermore, if you used a temperature scale that decreased to zero as the heat content decreased to zero, then the relationship between temperature and heat content could be represented as a simple ratio. This became the operational definition of a newly conceived property of systems, a property which came to be know as entropy. (The term was coined in 1865 by Rudolf Clausius who thought of it as representing a kind of "internal work of transformation".) Simply stated, entropy is the relationship between the temperature of a body and its heat content (more precisely, its kinetic heat energy). Entropy, S, is the heat content, Q, divided by the body's temperature, T.
S = Q/T
Stated another way, the heat, Q, stored in an object at temperature, T, is its entropy, S, multiplied by its temperature, T.
Q = T x S
That is it. The definition of entropy, as originally conceived in classical thermodynamics, had nothing to do with order or disorder. It had everything to do with how much heat energy was stored or trapped in a body at a given temperature. Think of it this way. If you removed all the heat energy possible from an object by cooling it down as far as possible (down to absolute zero), and then kept track of the heat you had to put back into it to bring it back to a given state, that amount of heat supplied divided by the final temperature in kelvin would be the entropy of that object in that state. The entropy of system is the average heat capacity of the system averaged over its absolute temperature.
The Significance of Entropy in Classical Thermodynamics
The significance of entropy in the study of heat engines and chemical reactions is that, for a given temperature, a system can hold only a certain amount of heat energy - no more and no less - depending on the entropy of the system. If the entropy of the system changes, some energy will be released or absorbed in one form or another (like a sponge that suddenly changes how much liquid it can hold). For heat engines that meant that if you wanted to convert heat into mechanical work, you needed to make sure that more heat flowed out of the hot reservoir than could "fit" into the cold reservoir. You did this by not letting the cold reservoir heat up as heat flowed in and by not letting the hot reservoir cool down as heat flowed out. As long as you maintained a temperature difference, more heat would flow out of the hot body than could be absorbed by, "fit into", the cold body. The surplus heat flow could be used to do mechanical work.In chemistry entropy meant that calculating the change in chemical energy, the energy represented by the making and breaking of chemical bonds, was not enough to predict how much useful energy would be released during a reaction. The amount of energy "freed" by a reaction was the energy generated by the chemical reaction minus any additional energy trapped by changes in the system's entropy. The additional energy trapped was just the change in entropy, delta S, times the temperature of the system, T. In 1876, J. Willard Gibbs named this useful energy released as "free energy" and provided the formula to calculate it. The free energy, delta G, was the change in chemical energy, delta H, minus the trapped, thermal energy, T times delta S.
delta G = delta H - (T x delta S)
Entropy According to Statistical Thermodynamics
So where then did the association between entropy and disorder come from? With time, more was learned about the role of molecules in determining the classical thermodynamic variables such as pressure, temperature, and heat. Pressure, it turned out, was just the total force exerted by individual molecules, colliding with themselves and the walls of the container, averaged over the surface area of the container. Temperature was determined to be the average kinetic energy of all the different ways the molecules could move, tumble or vibrate. This more detailed, molecular, perspective of thermodynamics and the mathematics associated with it became known as statistical thermodynamics.The person most responsible for working out the mathematical relationship between entropy and molecular movement was Ludwig Boltzmann. From the molecular description of heat content and temperature, Boltzmann showed that entropy must represent the total number of different ways the molecules could move, tumble or vibrate. The idea was that heat was just kinetic energy on a scale that could not be observed directly but that manifested itself in the aggregate as the thermodynamic properties that could be observed. Heat flowed from a hot body to a cold body as kinetic energy was transferred through molecular collisions occurring at the boundary between the two bodies and further distributed throughout the body as molecules collided with each other within the body. At each collision, kinetic energy was exchanged. On average, molecules with more kinetic energy lost kinetic energy as they collided and molecules with less kinetic gained kinetic energy as they collided, until, on average, the kinetic energy was optimally distributed among all the molecules and their various modes of movement.
The net result was that the more ways a system could move internally, the more molecular kinetic energy the system could hold for a given temperature. This was because temperature was just the average kinetic energy per mode of movement. You could think of these modes of movements as "pockets" that can hold kinetic energy. (You could also think of them in more technical terms as molecular oscillators or modes of thermal oscillation.) If each pocket, on average, could hold the same amount of kinetic energy, then the more pockets a system had, the more total kinetic energy the system contained. The greater the number of kinetic energy pockets a system had, the greater its entropy. So, on the molecular level, entropy was just a measure of the total number of molecular kinetic energy pockets contained in the system.
Entropy As Disorder
It was Boltzmann who advocated the idea that entropy was related to disorder. In Boltzmann's mind, the more ways a system could move internally, the more disorderly the system was. A system in "perfect order" was one in which all the molecules were locked in perfect array without any freedom of movement whatsoever. A dynamic system in perfect equilibrium represented, according to statistical thermodynamics, a system in "perfect disorder". The idea of entropy as a measure of disorder was embraced and perpetuated by his colleagues in the field of statistical thermodynamics.Problems With Entropy As Disorder
But is disorder really the best word to use to define entropy? I don't think so. There are several problems with using disorder to define entropy. The first problem has to do with systems having multiple levels of organization. A system might be more or less "orderly" on one level and not at all on another. Take the example of the ice cubes flying around in space. On the level of the ice cubes, the system is disorderly, but on the molecular level, the ice molecules are locked in place, neatly in order.There are two ways to deal with this ambiguity. One is to limit the application of the term to only one clearly specified level at a time. In doing so, we need to be careful as to what significance we attribute to entropy at the higher levels. These "higher entropies" cannot be taken as the total entropy of the system.
The other solution would be to reduce the whole system to its most fundamental level. The problem with this approach is knowing what is the most fundamental level of organization. At the time of Bolzmann and Clausius, molecules and atoms were considered to be the most fundamental level of organization. Now of course we know atoms have their own internal structure and even protons and neutrons have internal structure. So it gets very complicated to apply the statistical definition of entropy to any level of organization other than the original molecular level for which it was intended.
The second problem with disorder as a definition for entropy, in my mind, even on the molecular level, is that disorder implies things are not where they should be. This is not the case. Movement on the molecular level is still governed by Newtonian mechanics. If this were not the case, the equations correlating molecular movement with the observable variables of classical thermodynamics, such as temperature and pressure, could not have been derived as they were. The molecules are, in fact, exactly where they should be. Where else could they be? They are not free to make any random turn or jump between collisions. The rules are clear - continue straight between collisions and then strictly obey the laws of conservation of energy and conservation of momentum during the collisions.
Even if we limit ourselves to observable order, a system with high entropy can also have a high degree of order. Order depends not on how much movement there is in a system or the complexity of that movement, but on what significance the system's movement, or non-movement, has in the eye of the observer. If we could observe the individual sequence of moves of each molecule in a system and if a particular sequence had particular significance, for instance because it lead to a kind of replication or evolution, then we might perceive that combination of moves as having more order than some other combination.
Entropy should not and does not depend on our perception of order in the system. The amount of heat a system holds for a given temperature does not change depending on our perception of order. Entropy, like pressure and temperature is an independent thermodynamic property of the system that does not depend on our observation.
Entropy As Diversity
A better word that captures the essence of entropy on the molecular level is diversity. Entropy represents the diversity of internal movement of a system. The greater the diversity of movement on the molecular level, the greater the entropy of the system. Order, on the other hand, may be simple or complex. A living system is complex. A living system has a high degree of order AND an high degree of entropy. A raccoon has more entropy than a rock. A living, breathing human being, more than a dried up corpse.Answers to Pop Quiz
With this clearer understanding of entropy, let's take a look at those troubling entropy questions posed earlier. Those stacks of cards? They both have the same entropy. On the molecular level, the molecules are not behaving any differently in one stack than in the other. Even on the card level, there is no difference. None of the cards are moving. There is no kinetic energy present on the card level in either stack. There is no difference between the stacks except our subjective sense of order.As for the watch and the sundial, it depends. If they are both made of similar metals and they are at the same temperature and pressure, then on a molecular level they would have about the same entropy. The molecules in the watch would have about the same diversity of movement in the solid metal parts as the molecules in the metal of the sundial. Ounce for ounce, the heat content would be about the same for both.
On the higher system level, you could say the watch has more entropy than the sundial because it has a greater diversity of internal movement. The watch has more internal kinetic energy than the sundial. What significance you could give this "higher level" entropy is not clear to me.
The water in the stacked jars has more entropy than the flying ice cubes because liquid water molecules have more modes of movement than ice molecules. Again, the heat trapped in the liquid water per degree is greater than the heat trapped in the ice per degree. Certainly, the ice cubes have more kinetic energy observable on the macro scale and so could be assigned a kind of macro entropy, but what would that mean really? You could also calculate a kind of macro temperature along the same lines, as the average kinetic energy of the flying ice cubes, but why bother?
The Big Picture
So that brings us to the universe as a whole. This is very problematic. At the time of the Big Bang, there were no molecules. Is it really appropriate to talk about entropy, temperature and heat at this level? Does undifferentiated plasma have kinetic energy? What about the universe today? What is the temperature of the universe? What is the temperature of any system that is not homogeneous and not at thermal equilibrium? These are not trivial questions. The temperature and entropy of a system is only well defined for systems that are homogeneous and in thermal equilibrium. The easier way to answer the entropy of the universe question is to accept the 2nd law of thermodynamics and extrapolate backwards. The 2nd law says entropy is always increasing in the universe, so the entropy of the universe at the time of the Big Bang must have been much less that the entropy of the universe now.This does not mean there was more structure or order back then. It does mean there was less diversity and less space to move around. The evolution of the universe has been characterized by an on-going transformation from a simple, restricted, highly condensed, homogeneous state to an increasingly complex, widely dispersed, dynamic, multipotent, granular diversity. In other words, the universe is not winding down, like a giant soulless machine slowly running out of steam. On the contrary, she is just waking up.
Update: 11/16/2012
- I would like to thank all the readers who have responded positively to this article. I am pleased if I have succeeded in bringing you a little clearer understanding on the subject of entropy. I am also pleased to have found that I am not the only one trying to dispel the notion that entropy is disorder. Since first posting this article in January of 2011, I have discovered a collection of articles online by someone who has been arguing this very point far longer and with greater expertise than I. The author's name is Frank L. Lambert and he is a Professor Emeritus of Chemistry at Occidental College. You can find his articles on his web site at http://entropysite.oxy.edu/. For those of you seeking further explanation as to why shuffled decks and flying ice cubes do not represent higher entropy, I especially recommend Professor Lambert's Shuffled Cards, Messy Desks and Entropy is not "Disorder" .
- In my description of thermodynamic entropy I state that entropy is "the heat content, Q, divided by the body's temperature, T." This is not quite accurate. Entropy is certainly closely related to the total Q divided by the final T (see Frank Lambert and Harvey Leff, Correlation of Standard Entropy with Enthalpy ). However, the latter quantity, more accurately called the temperature averaged heat capacity, is not mathematically the same as entropy. Thermodynamic entropy is mathematically defined according to the Clausius relationship:
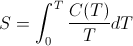
The temperature averaged heat capacity, on the other hand, is mathematically defined as:
where C(T) is the heat capacity as a function of temperature, T. The difference between the two expressions is in the placement of 1/T inside the integral as opposed to outside the integral. For constant temperature processes, 1/T is constant and can be moved outside the integral without affecting the computation. Thus for constant temperature processes such as phase changes, the melting of ice for example, the change in entropy is indeed the same as the change in the average heat capacity. However, the standard entropies, S0, one finds tabulated in physics and chemistry textbooks are not temperature averaged heat capacities, since they are calculated by integrating starting a 0 K up to the specified temperature. As Frank Lambert and Harvey Leff show, there is a strong correlation between the two quantities, but they are not the same thing. Unfortunately, thermodynamic entropy as defined by the above integral does not represent a simple, easily identifiable macro property of a substance. This is one reason the concept of entropy is so hard to teach. The closely related property of averaged heat capacity is much more intuitive and can be used as a stand-in for entropy in making the argument that entropy is not disorder, without invalidating the logic of the argument. Nevertheless, in hindsight, perhaps it would be better for me to borrow Professor Lambert's language and refer to thermodynamic entropy as "an index" of the averaged heat capacity rather than conflate the two concepts as one and the same.
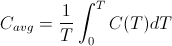





Comments