Hardy's Paradox explained (poorly) is that when a positron, antiparticle of an electron, and an electron go through the interferometers (see image below) simultaneusly, the two particles should meet in an "annihilation area" and destroy one another, but Hardy showed something else: quantum theory predicts that both particle and antiparticle could disturb, yet fail to annihilate, each other in the overlapping arms. Why? Because in the quantum world they can be both in and not in the overlapping arms.
"For nearly a century, the widespread interpretation of quantum mechanics suggests that everything is uncertain until it is observed, and that observation inevitably alters reality," says Professor Steinberg. "However, in the 1990s, a technique known as 'interaction-free measurement' seemed to promise the ability to 'see without looking,' as a Scientific American article put it at the time. But when Lucien Hardy proposed that one could never reliably make inferences about past events which hadn't been directly observed, a paradox emerged which suggested that whenever one attempted to reason about the past in this way they would be led into error."
Over the course of nearly two years of work, Steinberg and then-student Jeff Lundeen, now a research associate at the National Research Council of Canada, built a complicated quantum optical experiment and developed new theoretical tools.
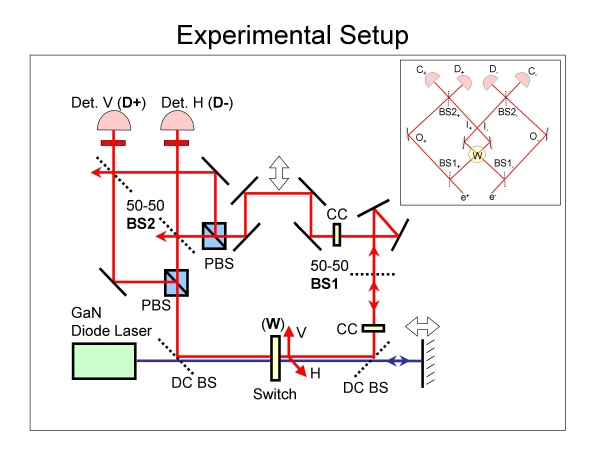
Thanks to the multiple existences of particles, they can simultaneously be in and yet not in the overlapping arms. Quantum theory allows an improbable yet entirely possible outcome that makes no sense. This is Hardy's paradox.
In essence, they combined Hardy's Paradox with a new theory known as weak measurement proposed by Tel Aviv University physicist Yakir Aharonov(2), showing that in one sense, one can indeed talk about the past, resolving the paradox. Weak measurement is a tool whereby the presence of a detector is less than the level of uncertainty around what is being measured, so that there is an imperceptible impact on the experiment.
"We found that all of the seemingly paradoxical conclusions in Hardy's Paradox can, in fact, be experimentally verified," says Steinberg, "but that the use of weak measurement removes the contradiction."
"Until recently, it seemed impossible to carry out Hardy's proposal in practice, let alone to confirm or resolve the paradox," he says. "We have finally been able to do so, and to apply Aharonov's methods to the problem, showing that there is a way, even in quantum mechanics, in which one can quite consistently discuss past events even after they are over and done. Weak measurement finds what is there without disturbing it."
Article: J. S. Lundeen, A. M. Steinberg, 'Experimental Joint Weak Measurement on a Photon Pair as a Probe of Hardy's Paradox', Phys. Rev. Lett. 102, 020404 (2009) DOI:10.1103/PhysRevLett.102.020404
ENDNOTES:
(1) Boschi, D, S Branca, F de Martini and L Hardy, “Ladder Proof of Nonlocality without Inequalities: Theoretical and Experimental Results”, Physical Review Letters 79, 2755 (1997)
(2) Yakir Aharonov, Alonso Boteroc, Sandu Popescu,Benni Reznika, Jeff Tollaksen, 'Revisiting Hardy's paradox: counterfactual statements, real measurements, entanglement and weak values', Physics Letters A Volume 301, Issues 3-4, 26 August 2002, Pages 130-138, doi:10.1016/S0375-9601(02)00986-6






Comments