Just as you thought it was over for 2011, and you proceeded to hung the Higgs mass plots on the christmas tree as a wish for stronger signals next year, ATLAS comes out with a new particle discovery. That's what I like of particle physics - there's always so much going on that the excitement is never really over.

The new particle is not anything we doubted should exist: it is a bound state of a bottom and a anti-bottom quark just as others we have found in the past 34 years (starting with Lederman and collaborators' discovery of the Upsilon); however, it is the first time that this particular state is seen, and this adds to our knowledge of heavy meson spectroscopy a small but not negligible bit of information. A small step for mankind, a boldface line in the CV of a few colleagues in ATLAS.

Let us see a bit more in detail what I am talking about first, and then how this discovery was made. First, the particle. Bottom quarks are the next-to-heaviest ones we know: they belong to the third generation of fermions, so they are close cousins to the top quarks. But while the top quark decays so fast that QCD interactions stand no chance of binding it to lighter ones, with the result that top decays as a free particle, the bottom quark lives long enough to form hadrons. If a bottom picks up a light quark it creates B mesons; if it picks two light quarks, it creates B baryons; and if it picks an anti-bottom quark, it creates "hidden beauty" mesons, b-antib pairs which are very simple systems, and whose behaviour is closely connected to that of positronium (the bound state of an electron and a positron).

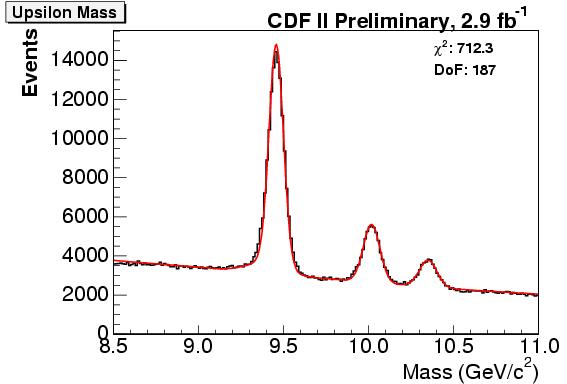In a "hidden beauty" hadron, the b and anti-b quarks orbit one around the other for a time long enough that the total energy of the system is well-defined; in other words, the hadron mass is then a very well-determined value: a narrow resonance! Examples of such states are the beautiful Upsilon mesons, which are readily reconstructed when they decay into muon pairs. See for instance the figure on the right, which shows how the CDF experiment sees the three lowest-mass such states, the Upsilon(1S), (2S), and (3S). The spectroscopic notation I am using labels states with different quantum numbers, and is entirely appropriate to do so, since these bound states  can indeed be distinguished by their angular momenta.

The chi_b states are different from Upsilons. They are still b-antib states, but they have zero total spin and a positive value of the "C-parity" quantum number. This makes the decay into muon pairs impossible at lowest order. The chi_b particles in fact have all been found in radiative decays of the Upsilon(2S) and (3S) states back to the lowest-lying states, with a subsequent decay to lepton pairs of the latter. In other words, what happens is that these states are like excited states of the Upsilon mesons, which quickly get back to the "fundamental" state by radiating off the excitation energy in the form of a photon; the resulting Upsilon particle then decays normally -in a sizable fraction of the case again by means of an electromagnetic transition to a lepton pair.

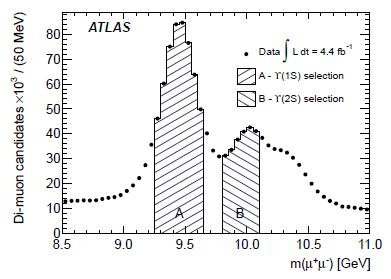ATLAS searched in fact pairs of muons making the mass of the Upsilon(1S) or (2S) mesons, and then looked around for an extra photon. Their capability to reconstruct the mass of muon pairs is not as good as the one of CDF, due to a worse momentum resolution; this is evident in the figure on the left (where hatched regions are the ones whose events are classified as Y(1S) and Y(2S) candidates, respectively).

However, ATLAS use a well-known trick to improve their mass resolution on the chi_b candidates: they compute it as M_(chi_b) = M(mu+ mu- gamma) - M(mu+ mu-) + M(Y). In other words, they subtract from the three-body mass the mass of the Y candidate they measure with low resolution, and add back the world-average measurement of the latter, thus improving the precision of the estimate.

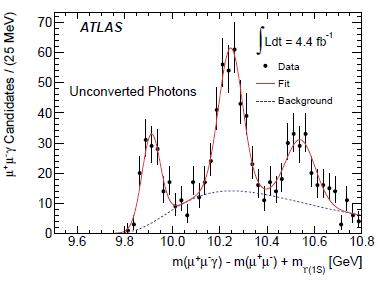On the right is the three-body mass spectrum obtained by ATLAS in their full 2011 dataset, using the Y(1S) candidates plus a photon. Three bumps are evident in the distribution: the ones due to the chi_b(1P) and chi_b(2P), and a third which does not correspond to any known resonant state. A significance in excess of six standard deviations is claimed for the third bump, which seems reasonable although it is probably very dependent on the assumptions made on the background shape.

A nice thing in searches including photons at collider experiments such as ATLAS and CMS, which shoot particles through "bricks" before these have a chance to be detected in the calorimeters, is that the photons have a very significant chance to convert into electron-positron pairs while they traverse the brick -pardon, the silicon tracker (the "brick" joke is due to my friend Larry Nodulman). In such cases, one can reconstruct the photon energy from the two tracks they yield, and this turns out to have a better resolution in energy than the calorimeter measurement. On the left below is the four-body mass spectrum that ATLAS derives from Upsilon (1S) and (2S) candidates added to electron-positron pairs: the peaks are much better defined, and the chi_b(3P) state is small but quite visible here as well.

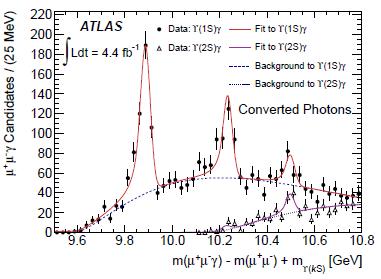So, my congratulations to the ATLAS colleagues for pulling this nice new resonance off - it is a beautiful small christmas present to human knowledge! If you want more information on the analysis, please see the preprint here.