Last Tuesday CDF announced their own discovery of the Omega_b baryon, a measurement which creates a controversy with the competing experiment at the Tevatron collider, DZERO. That is because DZERO had already claimed discovery for that particle, almost one year ago, and because the two measurements disagree wildly with each other. Just browse through my past few posts in this column and you will find all the information you need (how lazy can one be with links?).

I already discussed why the comparison of the two measurements shows that the one we have to abandon is DZERO's. Here, I will just conclude my test of the DZERO signal with pseudo-experiments -a technique I have already put at work in a previous post, where I showed that the claimed 5.4 standard deviations claimed by DZERO in their paper could not be more than 4.8 or 4.9.

Let us take the two measurements by CDF and DZERO at face value. DZERO claims that the mass is 6165 MeV, and assigns to that estimate a 10 MeV error from statistical sources, and a 13 MeV error from systematics. CDF claims that the mass is 6054.4 MeV, with a 6.8 MeV statistical and 0.9 MeV systematical uncertainty.

The first error in the two numbers above, "statistical", describes what is the constraining power of the amount of Omega_b candidates which was used for the measurement. It is a quite uncontroversial figure, which cannot be wrong under normal circumstances. The second error instead is an attempt to quantify how much the measurement conditions, the technique used, the peculiarities of the data, and other subtle effects may have impacted the determination of the mass, biasing it off its real value. Systematic uncertainties are typically hard to assess, and their proper handling shows the experience of the experimenter's hand.

The two mass measurements disagree by more than six standard deviations, but we can actually devise a means to determine how likely it is that one of them is right and the other is wrong. For, imagine that the CDF result is correct: you can now take the Omega_b mass as measured by CDF, the production rate as measured by CDF, and plug these numbers in a pseudo-experiment generation, asking the question of what could DZERO see in their data under such conditions.

The above recipe amounts to generating 79 events (plus or minus a few) by taking 5.99 of them from a Gaussian distribution, of width 34 MeV (DZERO's experimental mass resolution), and 73.01 from a flat background shape. After a suitable Poisson fluctuation, the resulting histogram can be fit "a' la DZERO". Under normal conditions, the fit will return what you have put in: a signal of about 6 events, sitting at 6054.4 MeV, give or take fifteen MeV or so.

Occasionally, though, those 6 events could be more, and they could conspire with a weird background fluctuation occurring at masses just above 6054 MeV, to create a signal which can be fit with a larger number of signal events, at a higher mass. Let me remind you that DZERO, in its mass distribution containing 79 events, fits 17.8 signal events. How often does that happen ?

Well, not quite often, indeed. In a hundred thousand pseudoexperiments, never does a 17.8 event signal appear at 6165 MeV or in its surroundings. The plot can be seen below.



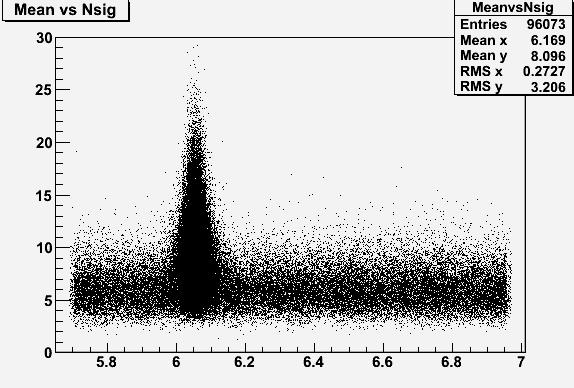
In the graph, every black point is a pseudoexperiment. The x-axis shows the fitted mass, and the vertical axis describes the number of fitted signal events. As you see, there is a large blob of pseudoexperiments where the fit gives the correct answer: a mass close to the generated one (6054 MeV or so), and a signal of 6 events -sometimes fluctuating up, even significantly so. Again, note that at the mass where DZERO finds its Omega_b, there are no pseudoexperiments finding a sizable signal. Also note that the fact that six out of 79 events were generated at 6054 MeV does not imply that the fitter won't sometimes choose a different fluctuation happening elsewhere in the spectrum: that is the meaning of the black band running around, with a fitted number of signal events happening to be centered at about 6 events by pure chance (it is a feature due to the number of generated data in the fitted histogram and the width of the signal which is sought).

The machinery we have put together can be used to investigate a slightly modified version of the question we posed above; a much more interesting one, in fact.

The most likely source of the CDF/DZERO discrepancy lies, as is typically the case, in not-well-controlled systematical uncertainties by one of the two experiments. So, suppose we were to inflate the systematic uncertainty in the DZERO measurement with a factor K; K=1 would be the default measurement, while K=2 would mean that the mass systematic quoted by DZERO was underestimated by a factor two. Now, by inflating the systematics, we can actually perform what is called a "convolution" of the results of pseudoexperiments shown above, with the experimental mass resolution of DZERO.

What I am getting at is the following: if DZERO measures a mass value with a large enough error bar, it would end up agreeing with the more precise CDF result. How large has this error bar become ? By how much do we have to blow up the DZERO systematics ?

We can solve the problem by taking a Gaussian function centered at 6165 MeV, with a width equal to sqrt(10^2+K^2*13^2) MeV, and adding together the value of this function at all mass values corresponding to pseudoexperiments that returned a number of signal events above 17.8. This number, divided by the total number of generated pseudoexperiments, is an estimate of the probability that DZERO observed a signal at 6165 MeV, with size of 17.8 events or larger, when the data contained a CDF-like signal instead. All this can be studied as a function of K, the "screw factor" affecting the 13-MeV systematic uncertainty assigned by DZERO to their mass measurement.

If you are confused about the procedure outlined above, do not worry -just believe me. I can explain the results and we can then try to interpret them. The result of the exercise is shown below. As you can see, for K=1 the probability that DZERO fitted 17.8 events at 6165 MeV, given a Omega_b producing 5.99 events in their sample at 6054.4 MeV, is very small, about one in 25,000. Very small, sure, but NOT a one-in-hundred-million as we thought by naively comparing the two mass measurements! This is a first thing to take home: if we assume that the CDF is right, AND that DZERO correctly assessed their systematics, this is a one-in-25,000 chance.



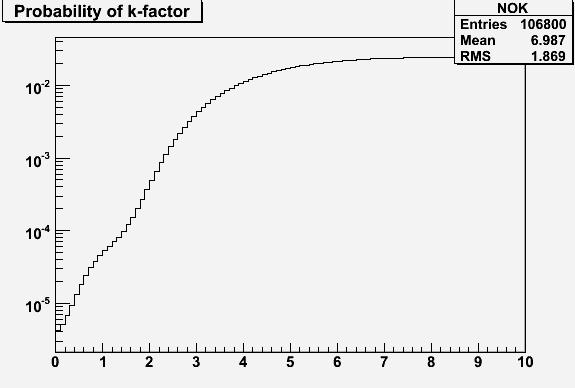
Now, look what happens if you blow up the DZERO systematics by a factor three: the probability rises to about one in 200! This is not so rare anymore...

Ok, so the two measurements are not altogether that incompatible, IF we assume that the CDF result is correct AND IF we are willing to admit that the DZERO systematics were assessed bit too happily.

Now, let us do the same exercise from the point of view of DZERO: that is, we assume now for a second that DZERO got mass and production rate right, and that CDF got a wrong result. This time, however, we have a problem. Since, in fact, the measured rate by DZERO is about twice as large as the one measured by CDF, we would have to insert in the CDF histogram not just six Omega_b events in 79, but 31 in 35! The CDF histogram contains only 35 events overall, most of which are for sure background ones.

Since the possibility that the CDF dataset contains 31 Omega_b events is so utterly impossible (by looking at the histogram) that we cannot even bring ourselves to running pseudoexperiments on such a hypothesis, we therefore have to try something different. We can assume that DZERO got the mass right, but the rate wrong. So we construct pseudoexperiments "a' la CDF" by taking 24.4 background events, distributed with a flat shape, and 10.6 signal events, distributed as a Gaussian with mean 6165 MeV (the DZERO measured mass), and with a width equal to sqrt(6.8^2+K^2*0.9^2) MeV: again, we insert a K factor to allow for a variation of the systematic uncertainties as measured by CDF.

The result of this exercise is shown below. You can see that the probability remains absolutely ridiculous even for a K factor of 10, which is really too much to buy, even for a much less careful experiment than CDF.



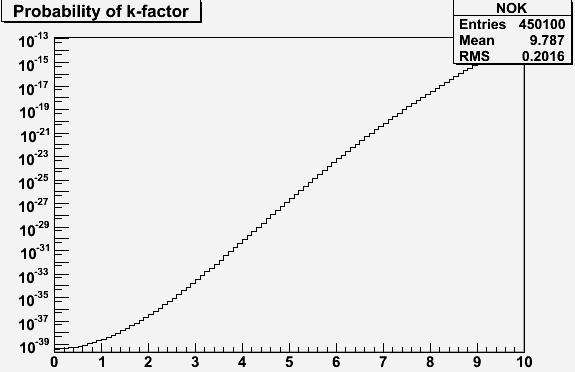
What to get from the above graph ? We find that the possibility that DZERO is right, and CDF messed up their mass measurement, is basically zero. So, of the two hypotheses, only one remains. And, as Sherlock Holmes once taught us, once the impossible has been ruled out, the remaining hypothesis, however improbable, is the true one.

Pseudo-experiments do not lie -at most, they can be done mistakenly, but they will usually give the right answer to a well-posed question. And I think I am now convinced, dear reader, beyond any reasonable or unreasonable doubt, that who discovered the Omega_b particle is CDF. However mildly unlikely it may look, DZERO probably picked up a fluctuation mixed up with the true signal, and heavily underestimated their mass systematics.