Time reversal and the weak force.I'd like to describe time reversal at a college freshman level. But first, let us wade through a little jargon. This jargon doesn't help with the explanation but is useful for relating this article to what you see in the literature.
Some jargon
"CPT" stands for the simultaneous application of three transformations of a description of a process in nature. The three transformations are: "Charge Conjugation", "Parity transformation", and "Time reversal". Under the assumptions of modern relativistic quantum field theory, CPT symmetry is a good symmetry of nature, that is, our best mathematical model of a quantum process is unaffected when we apply all three transformations to the model. The classic book on the subject is "PCT [or CPT], Spin and Statistics, and All That" by Streater and Wightman.
In this post we're concerned with processes whose models are changed under time reversal. In a slight abuse of the language, we say that such a process "violates time reversal symmetry", and is an example of "T-violation". Of course physicists cannot reverse time. The effect of "time reversal" on a process cannot be known to us; all we can test with this idea is our model of a process. Anyway, under the assumption that CPT is conserved, T-violation implies CP-violation. And the process (or model) we are discussing here is usually described in the literature as "CP-violation".
We will not need this jargon further. From here on we will be looking only at Time Reversal.
The Weak Force
Our best guess for a (not yet complete) model of the interactions of the basic elementary particles is called the "Standard Model". In that model, the only cause of time reversal violation is called the "Weak Interaction". It is the weak interaction that models the radioactivity of uranium and bananas.
The weak interaction is modeled with three "force carriers", the W+, W-, and Z particle. Of these, we're not concerned here with the Z and will talk about the W- only in as a sort of backwards moving W+. The proton and neutron are made up of "quarks". It is in the interactions of quarks with the weak force that time reversal appears in the Standard Model.
There are six whimsically named quarks {down, strange, bottom, up, charm, top} that we will refer to by their initial letters: {d,s,b,u,c,t}. Of these, the {d,s,b} have have electric charge -1/3 while the rest have electric charge +2/3. The difference in electrical charge between the {d,s,b} and {u,c,t} quarks is +1 and this is also the electrical charge of the W+ force carrier. And so it's possible for one d, s, or b quark to absorb a W+ force carrier and change into u, c, or a t quark. Since we begin with one of three {d,s,b} quarks and end up with one of three {u,c,t} quarks, there are nine possible interactions. And the odd thing is that all nine are possible.
So given that we begin with a d quark, we can end with a u, c, or a t quark. Experimentalists can measure only the three probabilities. It turns out that around 94.922% of the time we end up with a u quark, 5.076% of the time we get a c quark, and very rarely, about 0.001% of the time we get a t quark.
If we begin with an s quark we can still get a u, c, or a t quark but the chances change. We get a u about 5.071% of the time, the c shows up 94.76% of the time and we get a t around 0.168% of the time. Finally, if we beging with a b quark we mostly get a t quark but there's chances of getting the other two. This gives us 9 probabilities and we can fit them into a table of probabilities:
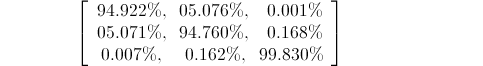
If the d quark absorbs a W+, it has to become one of the {u,c,t} quarks. So the top row of the above table adds to 100% (except for rounding). Similarly for the middle and bottom rows. But it's perhaps unexpected that this rule also applies to the columns. That is, the sum of the probabilities in the left column is also 100%, as is the sum of the middle and right columns.
Waves in Quantum Mechanics
If an interaction is seen in the deeply microscopic world, then the reverse of the interaction is also seen. This is alien to the world of human beings (where mothers give birth to babies but never reabsorb them), but seems to be universal in elementary particles. So one might say that a reason that the columns also sum to 100% is that the above table does double duty; in addition to telling the probabilities that apply when a {d,s,b} absorbs a W+ and becomes a {u,c,t}, the same table gives the probabilities when a {u,c,t} emits a W+ and becomes a {d,s,b}.
Quantum mechanics is a theory where quantum states have both a wave and a particle nature. So in modeling elementary particles, physicists must model a wave. The simplest waves are infinitely long waves with only a single frequency (plane waves) and these are the types that physicists prefer to use. At any given point, such a wave can be modeled by its amplitude (how high it is) and its phase (how advanced or retarded the wave is). A picture may be helpful:
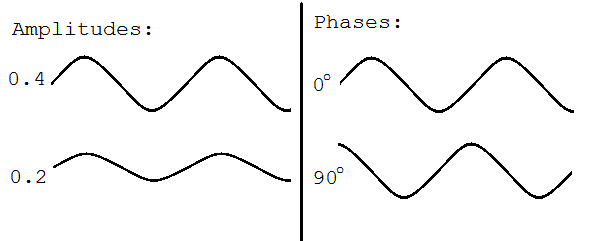
Complex numbers also have amplitudes (called "magnitudes", "absolute value", or "modulus") and phases (sometimes called "argument") and so are particularly useful in representing the amplitudes and phases of waves. This is true not just for quantum mechanics, the same use is made in the modeling of radio waves and sound waves.
The energy or intensity in a wave is proportional to the square of its amplitude. This is a fact true for all waves, so that the radio wavesintensity of a sound wave is proportional to the square of its peak pressure or its peak velocity. Similarly, in quantum mechanics the probabilities are proportional to the square of the amplitude of the quantum wave. Since the amplitude of a complex number is represented by vertical bars, so that the amplitude of X is |X|, physicists give the probability associated with X as |X|^2.
If all we had to model quantum states was literally just the complex numbers we wouldn't be able to distinguish the 6 quarks. In experiments, the {d,s,b} quarks can be distinguished from the {u,c,t} quarks by their electric charge, and the d, s, and b quarks are distinguished from each other by their different masses. Similarly u, c, and t; also have different masses. So in representing different quarks we need to get a little more devious than just the complex numbers.
Complex 3-vectors
The complex numbers have two attributes (which are real numbers), amplitude and phase. To distinguish the quarks we will need 6 times as many attributes. This is done by assembling complex numbers into vectors. We could do this with vectors with six components (called "6-vectors"), but instead we will simplify things a little and use 3-vectors to distinguish the {d,s,b} and another set of 3-vectors to distinguish the {u,c,t}.
The reason for using 3-vectors is that since a W+ interacts with a {d,s,b} to produce a {u,c,t}, it will be convenient to keep the {d,s,b} and {u,c,t} on the same footing. We will follow the physics "bra-ket" or "< | >" notation and specify the {d,s,b} vectors as the following complex 3-vectors:
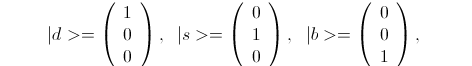
Note that the above three vectors are "orthogonal", that is, the complex dot products between them are all zero. This is a requirement for a set of completely distinguishable particles, in this case distinguished by their masses. Their masses can be determined by experimental observation so such a set of particles can be defined by the observable values of what the physicists call a "complete set of commuting observables". In this case there is only one observable; it is the mass. For this post we don't need to care what the mass is, just that it distinguishes the {d,s,b} and {u,c,t}.
We can observe the amplitude of a quantum wave: it's just the probability of finding the particle in that condition. So we simply run the experiment over and over until we get a good idea what the probability is. On the other hand, the phase is much more difficult to measure. The frequency of the waves is given by the wave's energy and Planck's constant, h. These frequencies are so high that we can detect them only when they interfere with themselves.
Wave Interference
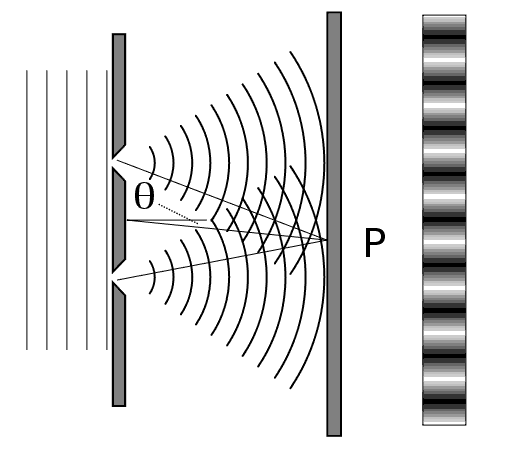
The interference of matter waves with themselves is directly seen in the double slit experiment. The wikipedia illustration shows waves moving to the right. When they hit the two holes, they spread out and interfere with each other on the right hand side:
Since we can't detect a quantum wave interfering with anything other than itself, our choice of model for the {d,s,b} is subject to arbitrary phases. For example, the following is another choice as valid as the previous:
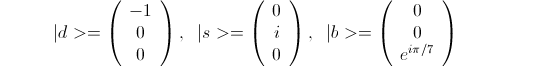
In the above, "-1" means that the wave is multiplied by -1. So it will be negative where previously it was positive and vice versa. This is a wave that whose phase has changed by 180 degrees. The "i" is the square root of -1, in the complex numbers this corresponds to a phase advance of 90 degrees. And the e^i pi / 7 in the definition of | b > means that the phase has been advanced by pi / 7 == 180/7 = 25.71 degrees. Note that in all three the amplitude is still 1.
Modeling Quarks under the Weak Force
Now we need complex 3-vectors for the {u,c,t} quarks, that is, we need to define {| u >, | c >, | t >}. We'd like to do this so as to make the W+ interaction be simple. Therefore we will assume that the W+ interaction takes a | d > and converts it to a |d'> that is a mixture of the {| u >, | c >, | t >}. Then we can use the rules of quantum mechanics to compute the probabilities in the matrix given earlier.
Probabilities in quantum mechanics are the squares of the amplitudes of complex numbers. Dot products produce a complex number (with amplitude and phase) so in computing the probabilities of getting the {u,c,t} we take the squares of the dot products. Writing the dot products as < u | d >, < c | d >, < t | d >, etc., the squares of their magnitudes are: | < u | d > |^2, | < c | d > |^2, etc., and according to the experimental measurements mentioned above we have:

The individual entries such as |< u | d >|^2 give the probability that the interaction takes this particular path, i.e. the d-quark absorbing a W+ to become a u-quark. And it also gives the probability for the reverse interaction, the u-quark emitting a W+ to become a d-quark. In the probability sense the interaction obeys time-reversal symmetry. However, in quantum mechanics we can also consider how the interaction changes the phases.
Finding Time Reversal
To see how the interaction changes the phases, we consider the dot product before taking the magnitude and squaring them, that is, we consider < u | d > instead of |< u | d >|^2. Since < u | d > is a complex number, it has both phase and amplitude so it's at least possible that the phase will be depend on which direction we go (from u to d versus d to u). Unfortunately, we can't measure phases so this experiment can't be done.
We can try to get around the phase problem by being sneaky. We can detect phases by interfering a particle with itself. So instead of considering just the d to u transition, let's also consider the u to d. We start with a d-quark. We arrange for it to have a 50% chance of absorbing a W+ (which changes it to a u-quark). Then we arrange for it to emit a W+ and so change back to a d-quark. (This is a wild journey for a quark and while it must happen gazillions of times per second we can't actually run this experiment cleanly. But we can talk about it.) Finally, we let the d-quark which played with W+s to interfer with itself:
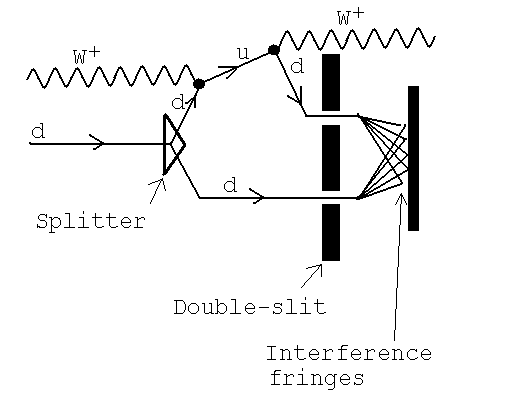
Unfortunately, the above experiment doesn't give any time reversal violation! The interference fringes, (if we could run the experiment!) would be unshifted from the usual. When we have a complicated sequence like the d-quark to u-quark to d-quark, we have to multiply the complex numbers associated with them (before we convert them to probabilities). And the complex number for the u-quark to d-quark is the complex conjugate of the complex number for the d-quark to u-quark. So when we multiply them we get < u | d > < d | u > = < u | d > < u | d >* = |< u | d >|^2. This is a real number and it's the same when we reverse the process. This might be clear given that the reverse process goes through the same sequence, d-quark to u-quark to d-quark.
The solution to this latest conundrum is to send the split quark through a more wild ride. The simplest sequence to send him through (that will keep electric charge conserved) is from d to u to s to c to d. Then the wild quark will absorb two W+s and emit two more. And when the sequence, "duscd", is reversed, we get a different sequence, "dcsud", and so this can (and does) show a violation of time reversal symmetry. The forward process, with its interference is:

The difference between the complex numbers for the duscd and dcsud sequences tells how much time reversal the sequence produces. Cecilia Jarlksog established the mathematics so the difference is called a "Jarlskog invariant", see PRL 55, 1039 (1985). For the case of the CKM matrix it is called "J_CP" as it defines the amount of CP-violation. Using the bra-ket language:
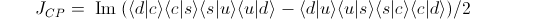
In the two products above, note that each quark appears once as a bra such as < d |, and once as a ket such as | d >. Since such pairs are related by complex conjugation, mathematically, this means that the unknown and arbitrary complex phases mentioned earlier are cancelled. For example, if we replace | b > with i| b>, then we have to replace < b | with -i< b |, and since (i)(-i) = 1, there will be no change to the product. In fact, products of bra-kets that begin and end with the same state such as < d | c >< c | s >< s | u >< u | d > and include bras and kets in pairs are a way of calculating "geometric phases". Even though they are (in general) complex valued, they are still observable. This source of phases were first explored by Sir Michael Berry and Shivaramakrishnan Pancharatnam and so are also called Berry-Pancharatnam phases. For a discussion of Berry-Pancharatnam phase in this form see "Geometric Phases by Péter Lévay (math-ph/0509064", particularly equation (18).
Maximum CP-Violation
A matrix of bra-ket products, organized by rows and columns such as:

is a "unitary matrix". We can always convert a unitary matrix into a matrix of probabilities by replacing each entry by the square of its amplitude. And given a matrix of probabilities it's possible to find (many) unitary matrices that give those probabilities. Unitary matrices also can be multiplied together to give another unitary matrix, that is, they are "closed under multiplication" and form a "Lie group".
Since J_CP uses the terms in this matrix, in looking for the maximum possible CP-violation we are exploring attributes of unitary matrices. It turns out that if a 3x3 unitary matrix (when converted to probabilities by squaring the amplitudes) gives all probabilities equal to 1/3, then a unitary matrix corresponding to it will give the largest possible CP-violation. Such a unitary matrix is sometimes called "democratic" as the probabilities are all equal.
Since the probabilities do not depend on the complex phases of the unitary matrix, there are a lot of different unitary matrices with the same probabilities. This gives experimenters a choice in how to represent this unitary matrix. These are called "parameterizations".
My paper now under review at Journal of Mathematical Physics gives a new parameterization for unitary matrices (in addition to giving the above description of CP-violation). The new parameterization is unique in that it treats all the "mixing angles" equally. The most famous of the mixing angles is the "Cabibbo angle". The Cabibbo angles gives the mixing between the up and down quark (it's responsible for the 5.07% probability in that first matrix given above). The other quark mixing angles are much smaller, but the neutrino mixing angles are quite large. With my new parameterization, the democratic unitary matrix becomes quite symmetric:
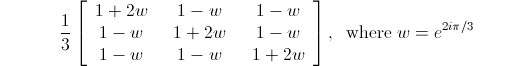
as opposed to the standard parameterization:
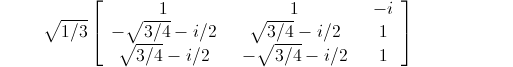
The new parameterization uses the permutation group of three elements and is based on the fact that if two matrices have all their rows and columns sum to one, then the product of the two matrices also has this property. Thus the new parameterization is the Lie algebra of a Lie subgroup of the unitary matrices.
The relationship between a Lie algebra and a Lie group is that the Lie group is obtained as the exponentials of the Lie algebra. Any element of the algebra defines a "one parameter subgroup". For example, the democratic unitary matrix given above (in the new parameterization) defines a subgroup of matrices of this form. That is, two matrices in the subgroup multiply to give another matrix. For example, the product of two matrices in the 1-parameter subgroup that includes the democratic mixing matrix is of the same form:
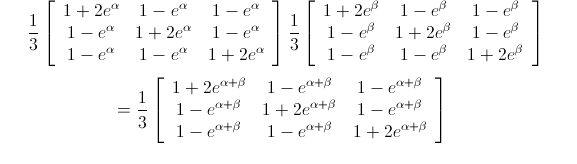
where alpha and beta are arbitrary imaginary numbers.
At least among members of the subgroup, the above gives a way of quickly doing multiplication using addition. For example, it's easy to write down an nth root of a unitary matrix this way. So the new parameterization has the advantages of both symmetry and easier calculations. The complete solution for all unitary matrices is given in my paper.





Comments