Five years ago I was fascinated by an analogy used by my friend Michelangelo Mangano to explain the problem of naturalness, a crucial issue in fundamental physics, and maybe the biggest single indicium we have that new physics beyond the standard model of particle physics should exist, and be not too far away from our current experimental reach.

Today I am preparing a talk at "ComunicareFisica 2012", a conference which is taking place in Torino this week, and I took on the issue of powers and limits of the analogy in the explanation of fundamental physics. So I found it natural to revisit Mangano's analogy, and in so doing I realized that it could be significantly improved. Before I discuss the improvement, let me state in short what the naturalness problem is.

The mass of the Higgs boson is known today: 125 GeV. Even before we measured it, however, we knew it had to be in that ballpark - indirect proof was already around. From a theoretical standpoint, however, it is hard to understand why it is not orders and orders of magnitude larger. There are, in fact, quantum corrections to the Higgs boson mass that arise from diagrams involving loops of virtual particles. It is as if the Higgs "dresses up" by continuously emitting and reabsorbing virtual particles, and this occupation affects its mass.

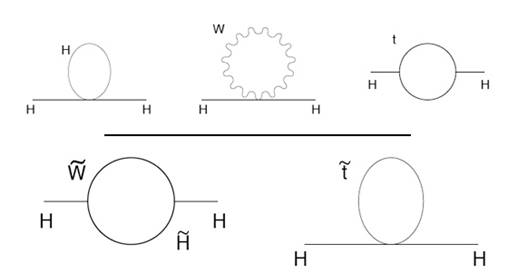Now, the magnitude of these corrections (there are a dozen of them, both positive and negative) must be enormous, if we allow the virtual particles in the quantum loops to have any value of momentum, up to the Planck mass scale (an energy scale of quadrillions of TeV). But their combined effect magically cancels to very high accuracy, leaving the Higgs mass at a "mere" 125 GeV. This fact has been taken to imply that there must exist a cut-off in the available range of momenta of the virtual particles in the quantum loops. The logical explanation of the physical origin of such a maximum value is the fact that at those very high energies some unknown new physics turns on.

Mangano thus cooked up the following analogy:

"Imagine to ask ten friends to give you each a irrational real number in the range ]-1,1[. You take the ten numbers and compute their sum, discovering that the result differs from zero only at the thirtifourth decimal place (0.00000....00001).
What do you conclude ? Are you willing to believe it a chance, or you take it as evidence that your friends conspired somehow for that result to come up ?"

If we examine this analogy we notice that it is not clear what is its deductive power. What is there in the target (the ten friends and the summing game) that is known, and which is unknown in the source (the quantum corrections) ? The tiny probability that the sum of large numbers gives a small result is not a concept requiring an analogy to be absorbed. The listener is certainly capable of considering the game of 10 numbers, but that system has nothing in common with quantum corrections to the Higgs mass which is easier to comprehend there. Moreover, taking a ]-1,1[ interval may be elegant, but gets us farther from the idea of the enormity of the cut-off at the Planck mass.

By virtue of having identified the shortcomings of Mangano's analogy, we can improve it by constructing a target which have as a parameter the dimension of the ten numbers: from the smallness of their sum we can then deduce the dimensions of the parameter, and the need of a small cut-off. Here is my bid, then:

"Imagine that Bob, a friend of yours, plays no-limits roulette, betting sums on red ten times. Each amount is determined at random, but all are smaller of a pre-determined maximum number M; Bob does not tell you what M is though.
After the ten bets Bob has one less dollar than he originally had in his pocket. What can we deduce on the maximum M ? May we believe it was M= a quadrillion dollars ? Of course not! We are led to believe that M was equal to just a few dollars."

[If you need a precise stipulation: The ten amounts can be thought to be given by a call to the root function gRandom->Uniform(0,1): that is each of them is x_i = y_i*M, with y_i a random number chosen with a flat probability distribution between zero and one.]

This analogy is better than the original one because it allows us to understand more quickly how theoretical physicists deduce that there must exist a cut-off, new physics at an energy scale not so much higher than the mass of the Higgs boson itself. The focus of the analogy is here not so much in the paradox of large numbers canceling each other -which is easy to explain even just considering the source- but on the inference we can draw on the magnitude of M.