The fact that the result I pick comes out in print quite some time after its first circulation in conferences, and the fact that the exclusion limits it presents are already well surpassed by earlier "preliminary results" already appeared at conferences, highlights the trouble that the LHC experiments are facing nowadays: the steep increase in integrated luminosity of proton-proton collisions they are delivered by the giant machine makes every result outdated by the time it sees the light of printed matter. What was new yesterday is already old today! Not to mention if things leak out before it's time to show them... Nonetheless, I observe that this is definitely a good problem to have! After years of painful wait for collisions, ATLAS and CMS (and LHCb and ALICE) are now breath-shortened by the pace that the machine has taken.
So, enough said about that. The result I want to discuss comes from a CMS search for Supersymmetric signatures involving a energetic charged lepton (electron or muon), missing energy, and four jets. This final state, which is quite typical of the decay of top-quark pairs (when one top decays to three hadronic jets, and the other decays to a jet and a lepton-neutrino pair), can also arise in several flavours of Supersymmetric signatures, which are the focus of the search. Of course, the top pair background is reduced by optimized kinematical cuts before a comparison of data yields and expected total backgrounds can reveal whether the SUSY process needs to be included in the mix to explain the observation. But the analysis has a specific interesting feature which makes it different from many others.
Two Words on Missing Energy
You need to know that missing transverse energy (aka "missing Et"), which is maybe the most powerful signature of the SUSY signal with respect to the two dominant backgrounds of top pair production and W+jets production, is a variable which needs to be treated with care. It is defined as the magnitude of the vector which you obtain by adding up all transverse momentum vectors of observed particles emitted in the collision: since the protons which collided carried no component of momentum in the plane orthogonal to their flight direction (the beam line), their products must also globally contain no transverse component, lest a very basic rule of dynamic be violated -conservation of momentum. So you expect to observe a value compatible with zero missing transverse energy in a collision, except when one or more energetic, non-interacting particles escape undetected, carrying away some momentum. Missing energy allows us to "see" these invisible bodies!
In top pair decays or W+jets production yielding the signature we discuss today, it is a single neutrino from W decay which is responsible for a significant missing transverse energy. In SUSY events, instead, one typically has two energetic neutralinos. Being the end result of a long decay chain, neutralinos usually carry a significant amount of momentum, making missing Et a golden signature.
Correlations are the Key
Being a quantity which depends on the details of the measurement of many others (the transverse energy of all the visible objects, be they jets, leptons, isolated tracks, etcetera), the missing Et is usually hard to model well with simulations. In this analysis a novel technique, first described in [1], is used to determine the expected shape of the missing energy from the shape of the momentum spectrum of the charged lepton which is also contained in the selected events.
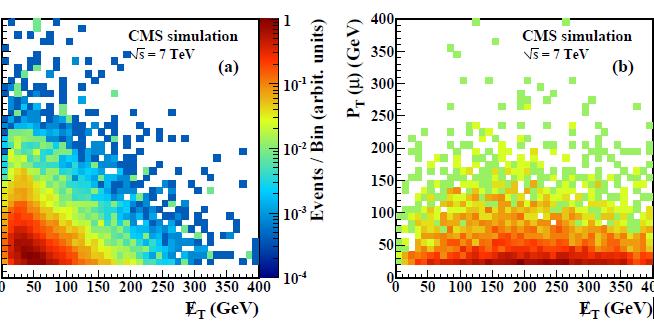
The relationship between lepton Pt and missing Et is clear in the figure above, which displays their scatterplot for simulated top pair production events and W+jets events (left), and in SUSY events (right). Let us focus on the panel on the left now, where the missing Et is indeed due to a single neutrino produced together with the charged lepton. Since the two bodies (the lepton and the neutrino, the latter producing missing Et) come from the decay of a W boson, there is an inverse correlation between their magnitude. You can observe indeed that the higher the missing Et, the lower is on average the lepton Pt, and vice-versa. This means that one can infer the distribution of missing Et one should see in these background processes from the shape of the lepton Pt distribution. We trust much more the lepton Pt shape of simulations than those of missing Et, because the former is less sensitive to instrumental effects and other nuisances; the trade-off is the fact that we need to understand the effect of some physical sources of uncertainty affecting its modeling.
Various effects need to be accounted for, in fact: the polarization of the W bosons -both in top and in W+jet production-, which directly affects the transverse momentum of the decay leptons; the different resolution of lepton Pt and missing Et; and the effects of the selection cuts on the two variables. But a detailed study can gauge the effect of all these systematical sources, controlling their impact on the predicted missing Et shape.
Besides the study of missing Et, the analysis is quite complex, and hard to describe fully in a blog posting. In a nutshell, CMS manages to define some "search boxes" as a function of the total visible transverse energy (Ht, basically the scalar sum of all the observed bodies -the same vectors which are used in the missing Et calculation, here however considered as single numbers summed linearly) and the value of missing Et divided by the square root of the Ht. The square root of the Ht is indeed a sort of "normalization factor" to determine how large the missing Et is, in a sense relative to the total amount of transverse energy displayed by the event. This is an interesting concept and I will allow myself a small deviation to clarify it.
A Note on Missing Et Resolution
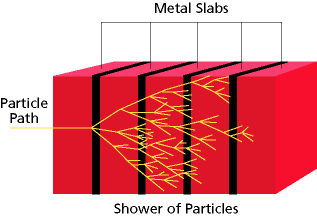We measure transverse energies in the calorimeters. Calorimeters are designed to gradually degrade the energy of an incident energetic hadron by a chain of nuclear collisions that the latter undertakes with the heavy passive material. As the incident particle hits nuclei, it creates a swarm of secondary hadrons. Each produced hadron of sufficient energy can in turn create another nuclear collision (see picture on the left); the active material in the calorimeter (usually multiple slabs of scintillating material) records the light yielded by the many particle crossing it. Of course, the more particles cross the scintillator, the larger the light output: from the magnitude of the latter, the number of secondaries can be determined, and this is, unsurprisingly, proportional to the energy of the incident primary hadron.Now, the above mechanism explains why the resolution on the measured energy scales with the square root of the energy: that is because of the Poissonian nature of number fluctuations in the produced hadrons -and thus of the light yield. In Poisson statistics, to a count N you must associate an error equal to sqrt(N). Ultimately, to the energy measured in a calorimeter you end up associating an error proportional to the square of the incident energy, because N is proportional to E, and the error on E depends on the fluctuations in N, which go with sqrt(N).
Once you know that a quantity is different from zero for your signal, you want to know how different from zero it is in your selected events. That is what analysts in CMS do: they just divide the missing Et by the estimated uncertainty sqrt(Ht), obtaining Y_MEt, a number which better tells you whether you observe the result of escaping particles or not.
In the figure on the right you can see how the Y_MEt distributes for selected events containing a muon, four jets, and missing Et>25 GeV, after a Ht>300 GeV cut. The sum of backgrounds agrees with the data (black points), whereas Supersymmetric particle production according to the "LM1" choice of parameters would produce an excess with the shape displayed by the empty black histogram. This has indeed a different shape in Y_MEt than the sum of backgrounds, but the contribution is not large -in fact, the "LM1" point lays at the edge of the region of sensitivity of the CMS analysis, as you will see below.Results of the Analysis
Needless to say, CMS finds good agreement between the observed events with large Y_MEt (the missing Et divided by the square root of Ht) and the predicted backgrounds. From the agreement, a statistical technique allows to decide what is the maximum number of SUSY events which the data might contain, given that we observed no excess. Accounting for luminosity and acceptances, these upper limits on SUSY event numbers are translated in a single yes/no information for each SUSY parameter space point: if the limit is smaller than what theory would predict for the considered set of SUSY parameters, that theory is excluded. The result is shown in the figure below.
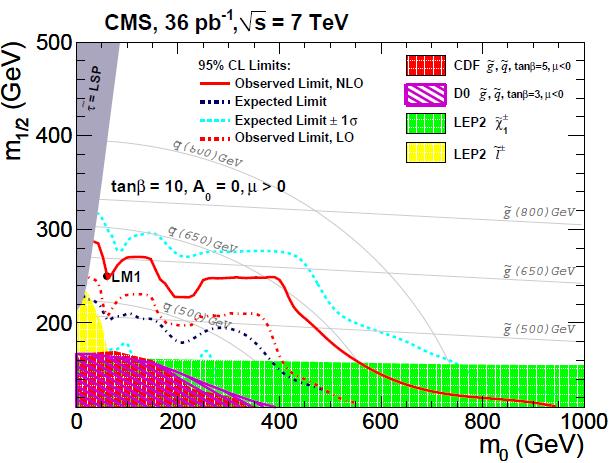
In the graph the two axes contain m_0 and m_1/2, which you can just take as two of the very many parameters describing the various SUSY theories. The CMS limit (full red curve -ignore the others, they are just a bit too confusing to my taste in this figure) excludes that these quantities take values to the left and below the curve. The limit is compared with other published results (areas in green, purple, grey, and yellow) for the particular subset of models denoted "CMSSM", a constrained version of the minimal supersymmetric extension of the standard model, and for a particular choice of the important parameter named "tan beta".
What we learn by the limit is, huhm, not much -but it is important to exclude these space points. They tell us that if the universe is really supersymmetric, it was born from a rather special set of initial conditions... And I will never get tired to note that for a Bayesian-thinking brain, the more we exclude of the SUSY space, the smaller must get our degree of belief of the correctness of SUSY!
[1]: V.Pavlunin, "Modeling Missing Energy in V+jets at the CERN LHC", 2009.
Comments